混合効果モデル、反復測定分散分析
ランダム効果と固定効果
通常の線形回帰モデル
通常の線形回帰モデルは、目的変数 $y_i$を説明変数 $x_i$ と誤差項 $e_i$ を用いて説明します。モデルは次のように表されます
$y_i = \beta_0 + \beta_1x_i + e_i$
ここで、$\beta_0$ は切片、$\beta_1$ は傾き（$x_i$ の効果）を表し、これらは固定効果です。誤差項 $e_i$ は、通常、平均 0 と一定の分散を持つ正規分布に従うと仮定されます。このモデルでは、$\beta_0$ と $\beta_1$ の固定効果をデータから推定します。
線形混合効果モデル
このモデルでは、切片と傾きにランダム効果（変量効果）を加えることで、データ内のグループ間の変動を考慮します。モデルは次のように拡張されます：
$y_i = (\beta_0+\alpha_0) + (\beta_1+\alpha_1)x_i + e_i$
$y_i = \beta_0+\beta_1x_i+(\alpha_0+\alpha_1x_i)+e_i$
ここで、$\alpha_0$ はランダム切片、$\alpha_1$ はランダム傾きを表し、これらはそれぞれのグループや個体が持つ固有の変動を捉えるためのものです。$\alpha_0+\alpha_1x_i$ はランダム効果（変量効果）であり、これらも通常、正規分布に従うと仮定されます。
線形混合効果モデルでは、固定効果 $(\beta_0、\beta_1)$ とランダム効果 $(\alpha_0, \alpha_1)$ の両方を同時に推定します。こうして、データ内の固定された傾向とランダムな変動の両方をモデル化できます。そのため、これを「混合効果」と呼びます。
データの準備と要約
例題）20名の脳卒中患者に理学療法を6週間実施して、実施前（ベースライン）、3週後、6週後の各時点でのFIM得点に差があるかどうか、有意水準は5%で検証せよ。
僕が作った架空のデータで練習しましょう。例題の内容や結果については色々とご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。この例題は反復測定の解析になります。各観測時点のデータが独立していないので〇元配置分散分析で解析するのは間違いです。
データセット glmm をdatに格納します（ファイルの読み込み）
dat <- read.csv("glmm.csv", header=T, fileEncoding = "UTF-8")
$\blacksquare$ stage：ブルンストロームステージ
$\blacksquare$ period: 観測時点（bl=ベースライン、w3=3週後、w6=6週後）
$\blacksquare$ fim: FIM運動項目の得点
View(dat)
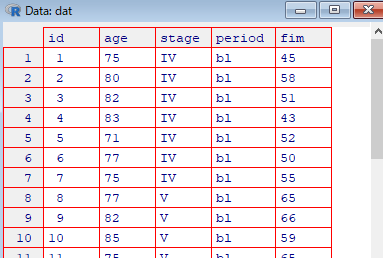
使用するパッケージ（パッケージのインストール）
#混合効果モデルのパッケージ
library(lmerTest)
library(nlme)
#混合効果モデルの多重比較
library(multcomp)
#tidyrとggplot2を使用
library(tidyverse)
#多重比較のためのパッケージ
library(multcomp)
変数の変更と基準の設定
ファクターに変更
#id, period, stageをファクターに変更
dat$id <- factor(dat$id)
dat$period <- factor(dat$period)
dat$stage <- factor(dat$stage)
基準の変更
# periodoの基準を bl に設定
dat$period <- relevel(dat$period, ref="bl")
# stageの基準を IV に設定
dat$stage <- relevel(dat$stage, ref="IV")
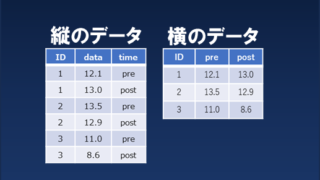
データの要約（縦のデータセット）
head(dat)
summary(dat)
dim(dat)
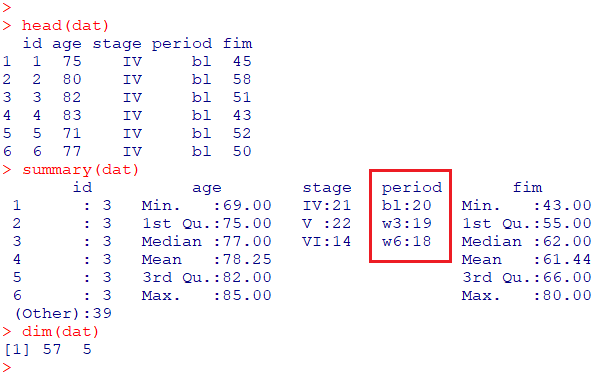
＊w3とw6に欠損があります
横データの作成
yoko <- tidyr::spread(dat, key=period, value=fim)
View(yoko)
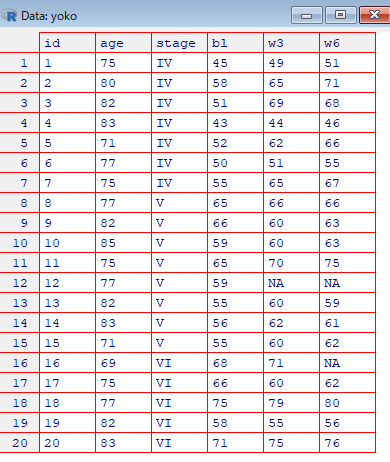
id12 の 3w, 6w と id16 の 6w の欠損が確認できます
グラフでデータを確認
# 基本的なグラフの設定
g1 <- ggplot2::ggplot(dat, aes(x = period, y = fim)) +
scale_x_discrete(
"観測時点",
labels = c(
"bl" = "ベースライン",
"w3" = "3週後",
"w6" = "6週後"
)
)
# ジッターの追加とテーマ性の設定
g2 <- g1 +
geom_jitter(height = 0, width = 0.1, size = 2) +
theme(
axis.title.x = element_text(size = 12),
axis.title.y = element_text(size = 12),
axis.text.x = element_text(size = 12),
axis.text.y = element_text(size = 12)
)
# グラフの出力
print(g2)
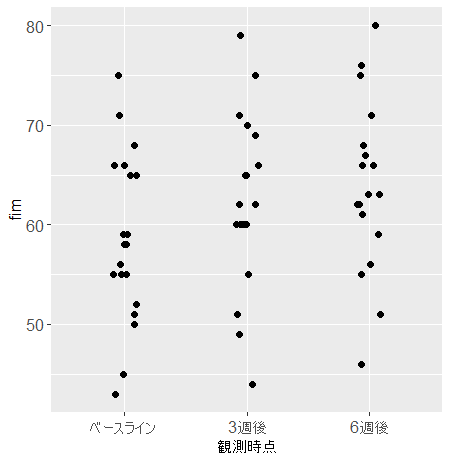
ネストしているデータ構造（マルチレベル）
上のグラフに stage と id の情報を追加します
g3 <- g1 +
geom_jitter(height = 0, width = 0.1, size = 3, aes(colour = stage)) +
geom_text(mapping = aes(label = id), vjust = 1.5)
print(g3)
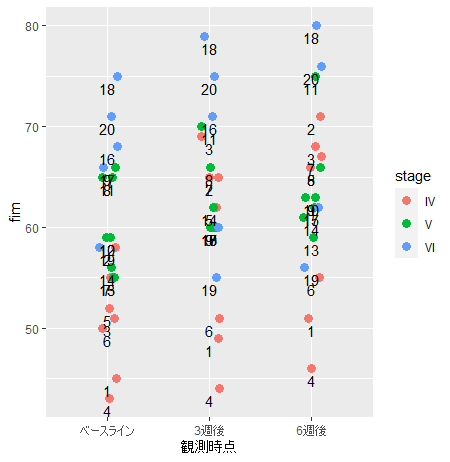
見づらい図ですが、おおよそこのようなイメージです（ageは記載してません）。これが「ネストしている」と言われるデータの構造です。図中の数字はidです（各観測時点で対応していることが理解できます）。
各stageごとに色分けして各時点を線で結びます。ただしデータを重ねて、IDは省略します。
# 基本的なグラフの設定とステージごとの色分け
g3 <- g1 +
geom_jitter(aes(colour = stage), height = 0, width = 0, size = 3) +
geom_text(mapping = aes(label = ""), vjust = 1.5)
# ステージの色に合わせて線を追加
g4 <- g3 +
geom_line(aes(group = id, colour = stage), linewidth = 1)
print(g4)
対応のあるｔ検定
3週目と6週目の差の検定を実行してみましょう（6週目－3週目）
これは対応のある2群の差の検定ですので、t検定で大丈夫です。ただし欠損しているデータが含まれているので、除外して検定しなければなりません。
id12とid16に欠損があるので、id12とid16のデータを削除して検定します
欠損のある対象者（id12, id16）とperiod=bl を全て除外したデータセット dat2 を作成
dat2
dat2 <- subset(
dat,
id != 12 & id != 16 & period != "bl"
)
summary(dat2)
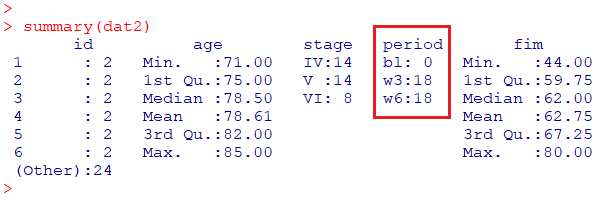
グラフ作成
#dat2を使用してグラフを作成
g4 <- ggplot(dat2, aes(x = period, y = fim, group = id, colour = id)) +
geom_line() +
scale_x_discrete(
"観測時点",
labels = c(
"w3" = "3週後",
"w6" = "6週後"
)
)
print(g4)
欠損値のある対象者（id12, id16）を削除したので、全て関連性があります
$\blacksquare$ 対応のあるｔ検定
横のデータセット yoko から欠損のある対象者（ id12 、 id16） を除外したセット yoko2 を作成（n=18）
# データyokoの行（12行目と16行目）を除外して新しいデータセットを作成
yoko2 <- yoko[c(-12, -16), ]
View(yoko2)
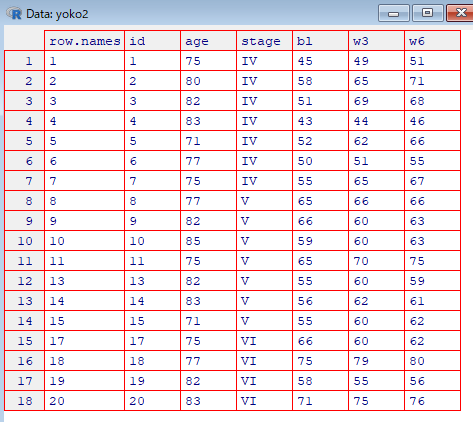
観測時点6週後と3週後のデータ間のt検定を実施
t.test(yoko2$w6 - yoko2$w3)
p<0.05で６週後のFIMが有意に高い結果となりました
混合効果モデル
反復測定分散分析（Repeated Measures ANOVA）と混合効果モデル
ANOVAにおいて、切片や傾きを被験者ごとに異なるランダム変数としてモデル化する場合、その分析は混合効果モデル（Mixed Effects Model）の一形態とみなされます。観測時点の効果を固定効果、各対象者の効果をランダム効果（変量効果）とした混合効果モデルを適用することで、各観測時点のデータの関連性を配慮した解析が可能となります。
例題を簡単なモデルにすると以下のようになります
$Y_{ij}=\mu+\pi_i+\gamma_j+b_i+\varepsilon_{ij}$
$i=1,…,n_j \quad j=bl, w3, w6$
$n_{bl}=20,\, n_{w3}=19, \, n_{w6}=18$
$\mu:$ 母平均
$\pi_i: $ 対象者 $i$ が属する群の効果（この例では stage や age の固定効果）
$\gamma_j:$ 時期の固定効果 $\quad$ j=bl (ベースライン),$\,$ j=w3 (３週間後),$\,$ j=w6 (6週間後)
$b_i: $ 対象者 $i$ の変量効果（各対象者 $i$ のばらつき） $\quad \sim N(0,\, \sigma_{id}^2)$
$\varepsilon_{ij}:$ 誤差（各対象者 $i$ の各観測時点 $j$ における効果） $\quad \sim N(0,\, \sigma_e^2)$
通常の線形回帰モデルは、固定効果のパラメータ（$\mu, \pi_i, \gamma_j, \varepsilon_{ij}$）のみを推定するために使用されます。このモデルでは、対象者の効果を表すランダム効果 $b_i$（または変量効果）が正規分布を仮定した確率分布としてモデル化されます。固定効果とランダム効果の両パラメータを推定するために、混合効果モデルと称されます。
混合効果モデルによる対応のある2群の比較
欠損値をカットしたデータセット dat2 を使用
対象者のデータが反復して測定されているので、対象者をランダム効果（変量効果）としてモデルに投入します
# lmer関数を使用した線形混合効果モデルによる解析
fit1 <- lmer(
fim ~ period + (1 | id), # (1 | id) これで対象者をランダム効果として指定
data = dat2
)
# モデルの要約を表示
summary(fit1)
固定効果の結果に着目
periodw6 の Estimate は 6w と 3w 差の平均値を示します
ｔ値、p値ともに 対応のあるt検定 と同じ値を示しています
欠損のある対象者も含めて解析
混合効果モデルを利用することで、欠損のある対象者も含めた解析が可能になります
データセット dat の period=3w, 6w を抜き出したデータセット（dat3）を使用
dat3
# datからbl（ベースライン）を除いたデータセットdat3を作成
dat3 <- subset(dat, dat$period != "bl")
summary(dat3)
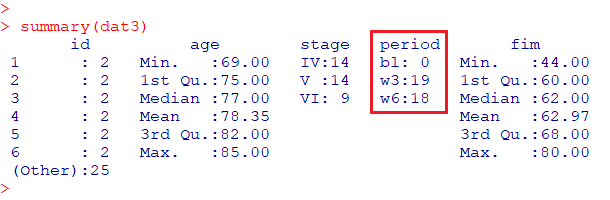
混合効果モデル
# lmer関数 を使用して混合効果モデルで解析
fit2 <- lmer(
fim ~ period + (1 | id),
data = dat3
)
# モデルの要約を表示
summary(fit2)
欠損値のあるデータを除外した場合とはやや異なる結果となります
経時データの相関
横のデータ（yoko）を使用
# yokoデータセットから"bl", "w3", "w6"のカラムを選択し、
# 上部パネルを削除して散布図行列を作成
pairs(
yoko[, c("bl", "w3", "w6")],
upper.panel = NULL
)
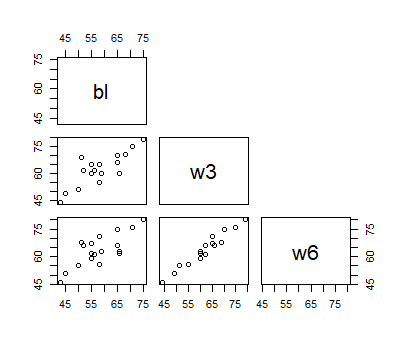
欠損しているデータを除いた yoko2 を使用
#分散・共分散行列
cov(yoko2[,c("bl","w3","w6")])
#相関行列
cor(yoko2[,c("bl","w3","w6")])
相関を考慮しなければならない理由
$\blacksquare$ 検定力低下
相関を考慮しない場合、標準誤差（SE）の推定が不正確になる可能性がある（過大または過小な推定）
結果として、検定力が低下する可能性がある
例えば、対応のある２群（A1, A2）の差の不偏標本分散は・・・
$V[A2-A1]=V[A2]+V[A1]-2cov(A2, A1)$
対応ある２群の相関を無視してしまうと不偏標準偏差が間違った値となることが理解できます。証明については「確率変数の差の分散」などをキーワードで検索してみてください
$\blacksquare$ 偏りの問題
ランダム効果を無視すると、固定効果の推定値が偏る可能性がある
固定効果やランダム効果が過剰な値に推定される可能性があり、非常に小さい効果でも統計的に有意とされる可能性がある
$\blacksquare$ Type I エラーの増加
複数の比較（例えば、idごと、periodごと、stageごとなど）が行われる場合、それぞれの比較でType Iエラーが生じる確率が独立に高まる可能性が生じる
$\blacksquare$ 信頼区間の不正確性
上述した問題から信頼区間が不正確になる場合がある
切片モデル（ランダム切片モデル）
対象者ごとのランダム効果の切片の変動を取り入れて、そのばらつき（分散）を定量化するモデル
# lmerTestパッケージを使用して線形混合効果モデルを作成
model1 <- lmerTest::lmer(
fim ~ period + (1 | id), # 固定効果とランダム効果の定義
data = dat # 使用データセット
)
# モデルの要約を表示
summary(model1)
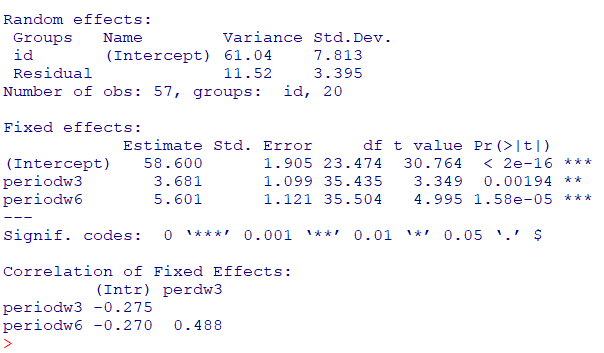
3週目とblには差があり、また6週目とblには差があることが理解できます
3Wと6Wの比較は基準を変更するか、多重比較で検定可能です
model1から分散分析表の算出も可能です
anova(model1)
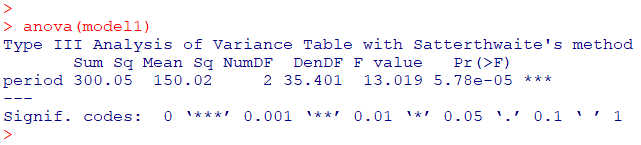
Random effects の Variance
ランダム効果の切片の分散：$\hat{\sigma}_{id}^2=61.04$（母分散を推定した分散）
Correlation of Fixed Effects (固定効果パラメータの相関行列)
固定効果のパラメータが互いにどの程度関連しているかを示す
# 固定効果パラメータの分散共分散行列を取得
cov_mod <- vcov(model1)
# 標準偏差を計算
std_mod <- sqrt(diag(cov_mod))
# 相関行列を計算
cor_mod <- cov_mod / (std_mod %o% std_mod)
print(cor_mod)
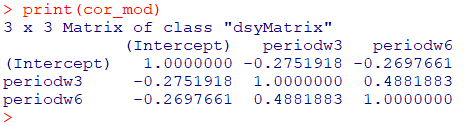
混合効果モデルの分散や相関行列の導出、またパラメータの推定や標準偏差の導出（Kenward-Roger、Satterthwaite）については、またの機会にアップしたいと思います。以下、ChatGPTの答えです。
切片・傾きモデル（ランダム切片、ランダム傾きモデル）
注意）
傾きを評価するためにperiodを連続変数として扱います（連続変数period_nを追加）
ベースラインを0、３週目を3、６週目を6と設定します
library(dplyr)
dat <- dat %>%
mutate(period_n = case_when(
period == "bl" ~ 0,
period == "w3" ~ 3,
period == "w6" ~ 6,
TRUE ~ NA_real_ # それ以外の場合はNAを代入
))
ランダム切片、ランダム傾きモデル
model2 <- lmerTest::lmer(
fim ~ period_n + (1 + period_n| id),
data = dat
)
summary(model2)
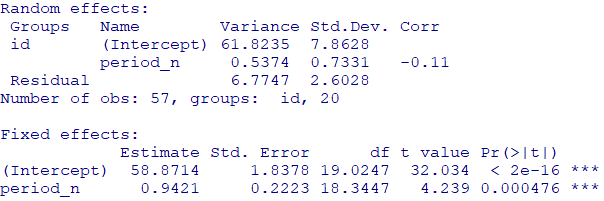
多重比較
periodに有意な効果を認めたのでmodel1の多重比較
mc <- multcomp::glht(
model1,
linfct = mcp(period = "Tukey")
)
summary(mc)
調整（bonferroni）
summary(mc, test = adjusted("bonferroni"))
以下の調整が可能
“single-step”, “Shaffer”, “Westfall”, “free”, “holm”, “hochberg”, “hommel”, “bonferroni”, “BH”, “BY”, “fdr”, “none”
複合対称型（Compound symmetry）
ここからはやや複雑になりますので、実際に解析されるときはお近くの統計の先生にご相談いただいた方が賢明かと思われます。
各観測時点における分散が等しく（等分散）、異なる観測時点間の共分散が等しいことを仮定したモデル
$\sigma^2=\sigma_{id}^2+\sigma_e^2$
$\rho=\dfrac{\sigma_{id}^2}{\sigma_{id}^2+\sigma_e^2}=ICC$（級内相関係数）
この仮定は、例えば反復測定における測定間隔が一定である場合や、クラスター内の観測値が同じように相関すると期待される場合などに適用されます
Compound symmetryは、モデルの解釈を容易にするためにしばしば使用されますが、解析対象のデータの共分散構造に適合しているか検証しなければなりません。適合していない場合は、モデルの適合度や推定結果に誤りが生じる可能性があります。
$cov(Y_{ij}) =
\begin{pmatrix} \sigma_{id}^2+\sigma_e^2 & \sigma_{id}^2 & \sigma_{id}^2 \\ & \sigma_{id}^2+\sigma_e^2 & \sigma_{id}^2 \\ & & \sigma_{id}^2+\sigma_e^2 \\ \end{pmatrix}$
$= \sigma^2 \begin{pmatrix} 1 & \rho & \rho \\ & 1 & \rho \\ & & 1 \ \end{pmatrix}$
lme関数による Compound symmetry を指定したモデル
model3 <- nlme::lme(
fim ~ period,
random = list(id = pdCompSymm(~ period)),
data = dat
)
summary(model3)
list(id = pdIdent(~ period))
(~ period) と書くと、切片も傾きもランダム効果となります。(~ period-1) と書くと、 -1 がランダム切片をモデルから除外することを意味することになり、対象者ごとのランダム傾きのみを持つモデルを指定します。
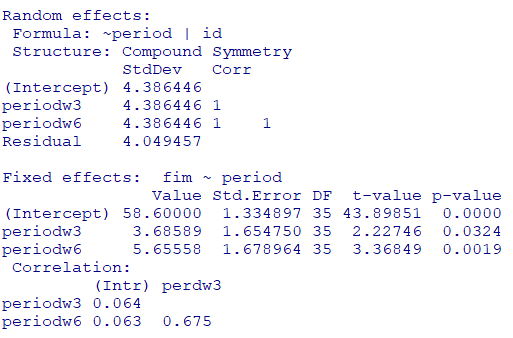
periodとstageの両方にCompound symmetry構造を想定した場合
model3_2 <- lme(
fim ~ period,
random = list(id = pdCompSymm(~ period), id = pdCompSymm(~ stage)),
data = dat
)
summary(model3_2)
AR1型
$\blacksquare$ 一次自己回帰モデル
$X_t=\phi X_{t-1}+\epsilon_t$
$X_t: $時点tにおける観測値\
$\phi: $自己回帰パラメータ
$\epsilon_t: $時点tにおける誤差項
AR1型の共分散構造は、一次自己回帰モデル(AR1)に由来しており、隣接する観測値間の相関が減衰するという構造を持っています
$Corr(X_t,X_{t−1})=\phi$
$\phi*Corr(X_t,X_{t−2})=\phi^2$
一次自己回帰モデル（AR1モデル）は、時系列データのモデリングで使用され、現在の観測値が前の時点の観測値に依存するという構造を持っています。AR1型の共分散構造は、一次自己回帰モデル(AR1)に由来しており、隣接する観測値間の相関が減衰するという構造を持っています。AR1型の共分散構造は、混合効果モデルや一般化推定方程式などで使用され、観測値間の相関をモデル化する際に、隣接する観測値間の相関が最も強く、次第に離れた時点間の相関が減少する構造になっています。
経時データの解析で使用される場合が多い共分散構造
最も隣接する時点（”bl” と “w3″）の相関が最も強く、次第に離れた時点（”bl” と “w6″）の相関が減少する共分散構造
$cov(Y_i) = \sigma^2 \begin{pmatrix} 1 & \phi & \phi^2 \\ & 1 & \phi \\ & & 1 \\ \end{pmatrix} $
例えば、AR1型の共分散構造において隣接する観測値間の相関が0.5の場合、1時点離れた観測値間の相関は0.5^2=0.25、2時点離れた観測値間の相関は0.5^3=0.125となる
ランダム効果の共分散構造は、対象者ごとの違いやグループ内の変動を捉えるために使用され、 random引数 で指定されます。観測誤差の相関構造は、隣接する観測誤差（モデルの予測と実際の観測値との差）の相関を考慮するために使用され、これは correlation引数 で指定されます。
観測誤差（モデルの予測と実際の観測値との差）の相関とは、例えば「blの予測値と実際の観測値の差」と「w3の予測値と実際の観測値の差」の相関ということです！
model4 <- lme(
fim ~ period,
random = ~1 | id,
correlation = corAR1(form = ~1 | id),# (form = ~1 | id) は、相関構造が個体idごとに存在することを示しています
data = dat
)
summary(model4)
Correlation Structureは、 AR1 の相関構造を示し、そのパラメータの推定値は 0.8214593 ($\phi=0.8214593$) であることを示しています。Correlationは、固定効果パラメータの推定値間の相関を示しています。
無相関型（indepedence）
切片のランダム効果を除外して、bl, 3w, 6wの各期間の分散が等分散であり、また各期間には関連性がない（無相関）ことを仮定したモデル
したがって、今回のような経時データの解析には適用できない場合が多いモデルです
$cov(Y_{ij}) = \begin{pmatrix} \sigma^2 & 0 & 0 \\ & \sigma^2 & 0 \\ & & \sigma^2 \\ \end{pmatrix} $
この共分散構造は、異なる期間同士のランダム効果が互いに無相関であるという仮定に基づいています
（~ period-1）の -1 で、各idのランダム効果の切片を除外して、periodに対するidのランダム効果のみを設定
# nlmeパッケージを使用して線形混合効果モデルを作成
model5 <- nlme::lme(
fim ~ period,
random = list(id = pdIdent(~ period - 1)),
data = dat
)
# モデルの要約を表示
summary(model5)
pdIdent関数は等分散の共分散構造を定義するための関数です。ランダム効果のすべての成分が同じ分散を持ち、他の成分との共分散が0であるという構造を持つため、実質的には対角行列となります。
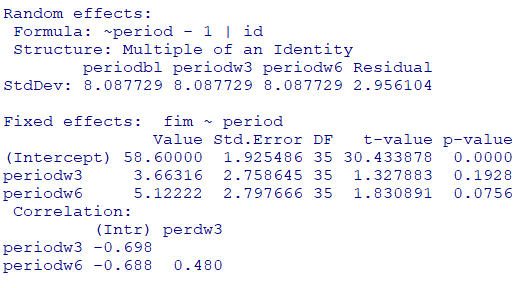
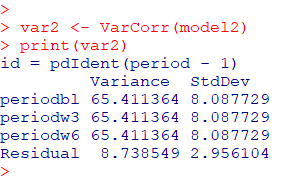
$\blacksquare$ 分散
$\sigma^2=8.087729^2＝65.41$
Rの関数は以下のようになります
var2 <- VarCorr(model5)
print(var2)
無構造型 (unstructured)
$cov(Y_{ij}) = \begin{pmatrix} \sigma_{bl} & \sigma_{bl, w3} & \sigma_{bl, w6} \\ & \sigma_{w3} & \sigma_{w3, w6} \\ & & \sigma_{w6} \\ \end{pmatrix} $
model6 <- nlme::lme(
fim ~ period,
random = list(id = pdSymm(~ period - 1)),
data = dat
)
# モデルの要約を表示
summary(model6)
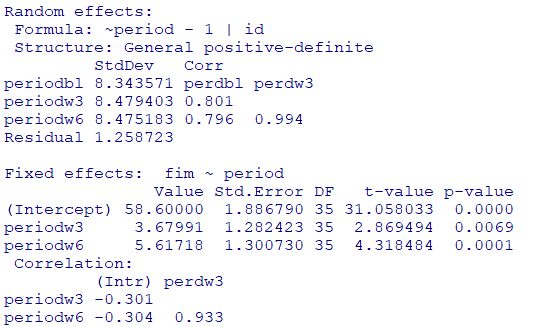
以下、ChatGPTの答えです
共変量で調整したモデル
$\blacksquare$ 混合効果モデルは重回帰分析と同様に多くの変数を投入して変数選択していくことも可能ですが・・・
# lme関数を使用して線形混合効果モデルを作成
# 期間、ステージ、年齢を固定効果として、個体差を複合対称構造でランダム効果として考慮
multi1 <- lme(
fim ~ period + stage, # 固定効果の定義
random = list(id = pdCompSymm(~ period)), # ランダム効果の定義（複合対称構造）
data = dat # 使用データセット
)
summary(multi1)
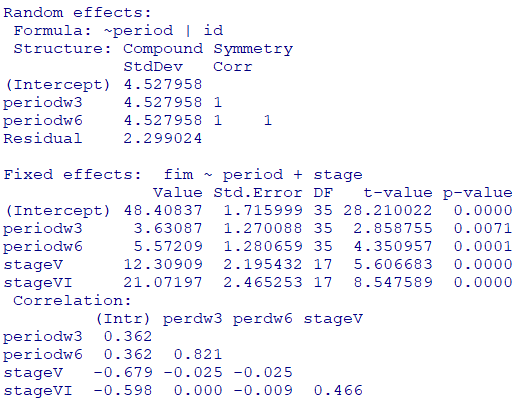
$\blacksquare$ 交互作用の効果も検証可能
multi2 <- lme(
fim ~ period * stage, # 固定効果の定義
random = ~ 1 | id, # ランダム効果の定義
data = dat # 使用データセット
)
# モデルの要約を表示
summary(multi2)
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください