Fisherの正確確率検定

2023.01.01

1ページ　2ページ　3ページ

データの準備と要約

Fisherの正確検定、Fisherの正確確率検定、Fisherの直接確率検定、Fisherの直接法などと呼ばれています。ここでは、Fisherの正確確率検定をタイトルとして使用します。

例題

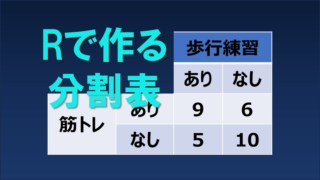
新たなトレーニング方法が開発され、運動障害を持つ患者（軽度群、重度群）に対して実施された。軽度群と比較して、重度群に対する新トレーニング法の効果について検証した。

オッズの定義

研究目的に応じてオッズ、オッズ比を定義してください

$オッズ=\frac{新トレーニングの効果あり}{新トレーニングの効果なし}$

$オッズ比=\dfrac{重度群のオッズ}{軽度群のオッズ}$

サンプル（架空のサンプルです）

障害レベル; severity（severe=重度, mild=軽度）
効果; effect（yes=あり, no=なし）

R
severity <- c(rep("severe", 12), rep("mild", 6), rep("severe", 3), rep("mild", 8))
severity <- factor(severity, levels=c("severe", "mild"))
levels(severity)
#[1] "severe" "mild"
effect <- c(rep("yes", 18), rep("no", 11))
effect <- factor(effect, levels=c("yes", "no"))
levels(effect)
#[1] "yes" "no" 
tab <- xtabs( ~ severity + effect)
print(tab)
> print(tab)
        effect
severity yes no
  severe  12  3
  mild     6  8
基準カテゴリー

factor() 関数は名義変数をカテゴリカル変数（因子型変数）に変換し、データのカテゴリーは「水準」として定義されます。levels() 関数で表示されるカテゴリカル変数の水準のうち、最初に表示されるカテゴリーがデフォルトで基準カテゴリー（参照カテゴリー）となり、統計モデルでの比較の基点として機能します。relevel() 関数や factor() 関数の levels 引数を使用することで、レベルの順序を指定し、基準カテゴリーを変更することが可能です。

重度群のオッズは$\frac{12}{3}=4$、軽度群のオッズは$\frac{6}{8}=0.75$となります。この比率が「1」か「1ではない」かということを調べるために、下記のオッズ比を利用します。

$オッズ比 =\dfrac{重度群のオッズ}{軽度群のオッズ}= 5.33$

5.33なのでオッズ比は1より大きい結果となりました。オッズ比が高くなると重度群の効果割合が軽度群の効果割合より高いことを意味します。

仮説

帰無仮説 H0: オッズ比＝1（重度群のオッズ ＝ 軽度群のオッズ）
対立仮説1 H1: オッズ比 > 1（重度群のオッズ > 軽度群のオッズ）➡ 上側検定
対立仮説2 H1: オッズ比 < 1（重度群のオッズ < 軽度群のオッズ）➡ 下側検定
対立仮説3 H1: オッズ比 ≠1（重度群のオッズ ≠ 軽度群のオッズ）➡ 両側検定

サンプルから考えると「仮説2」と「仮説3」は不要と思われますが、統計学備忘録として3つの仮説を取り上げます。

Rで分割表の作成

分割表の操作については、以下の記事を参照ください。

Rで作る分割表（クロス表）
リハビリテーション統計学でも頻繁に使用する分割表。Rを使用して表の操作や検定を実行します。
y2pt.com
2023.09.03

分割表の周辺合計

R
addmargins(tab)
> addmargins(tab)
        effect
severity yes no Sum
  severe  12  3  15
  mild     6  8  14
  Sum     18 11  29

周辺合計を固定した場合に、考えられる全ての分割表を求めます。

R
# Define a function to generate and display contingency tables
print_tables <- function() {
  total_severe <- 15
  total_mild <- 14
  total_yes <- 18
  total_no <- 11
  
  # Calculate the possible range of values for a
  # a corresponds to severe & yes
  for (a in max(0, total_yes - total_mild):min(total_yes, total_severe)) {
    b <- total_severe - a  # severe & no
    c <- total_yes - a     # mild & yes
    d <- total_no - b      # mild & no
    
    # Check if b, c, and d are all non-negative integers
    if (b >= 0 && c >= 0 && d >= 0 && c <= total_mild && d <= total_mild) {
      # Print only the contingency table
      cat(sprintf("Effect\n"))
      cat(sprintf("Severity   Yes  No\n"))
      cat(sprintf("Severe     %d   %d\n", a, b))
      cat(sprintf("Mild       %d   %d\n\n", c, d))
    }
  }
}

# Run the function to display all contingency tables
print_tables()
> print_tables()
Effect
Severity   Yes  No
Severe     4   11
Mild       14   0

Effect
Severity   Yes  No
Severe     5   10
Mild       13   1

Effect
Severity   Yes  No
Severe     6   9
Mild       12   2

Effect
Severity   Yes  No
Severe     7   8
Mild       11   3

Effect
Severity   Yes  No
Severe     8   7
Mild       10   4

Effect
Severity   Yes  No
Severe     9   6
Mild       9   5

Effect
Severity   Yes  No
Severe     10   5
Mild       8   6

Effect
Severity   Yes  No
Severe     11   4
Mild       7   7

Effect
Severity   Yes  No
Severe     12   3
Mild       6   8

Effect
Severity   Yes  No
Severe     13   2
Mild       5   9

Effect
Severity   Yes  No
Severe     14   1
Mild       4   10

Effect
Severity   Yes  No
Severe     15   0
Mild       3   11

考えられる分割表は12組あります。これでFisherの正確検定の準備は完了、有意水準5％で検定してみましょう。研究計画（何を立証したいのか）に従い、以下から適切な検定方法を選択します。

関数 fisher.test で検定を実行

> addmargins(tab)
        effect
severity yes no Sum
  severe  12  3  15
  mild     6  8  14
  Sum     18 11  29
片側検定（上側），alternative = “greater”

対立仮説1 H1: オッズ比 > 1（severe グループのオッズが mild グループよりも大きい）。これは、重度群の効果ありの人数が12人以上になる確率を求める検定です。

R
fisher.test(tab, alternative = "greater")
        Fisher's Exact Test for Count Data

data:  tab
p-value = 0.04601
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
 1.029929      Inf
sample estimates:
odds ratio 
  5.003853

X≧12、つまりX=12, 13, 14, 15 となる確率を求めます。
P(X) = P(X≧12 | severe=15, mild=14, yes=18 ) という条件付き確率になります。
P(X＝12) + P(X=13) + P(X=14) + P(X=15)＝0.046
この確率は超幾何分布を使って求めます(後で出てきます)。

p値 が0.046（p<0.0.5）のため、帰無仮説（重症群と軽度群の間に差がない）を棄却します。これは、重症群の効果が軽度群と比較して統計的に有意である可能性が高いことを意味します。

  • p-value（ｐ値）= 0.046
  • alternative hypothesis（対立仮説）: Rは対立仮説を出力します。ここでの対立仮説は、「真のオッズ比は１ではない」。すなわち・・・p値<0.05なので「重症群と軽度群には有意差があり、重症群のオッズは有意に高い」という結果になります。
  • 95 percent confidence interval: 下記のオッズ比の95%信頼区間。
  • odds ratio（オッズ比）5.003853: これは単純な割り算のオッズ比（5.33）ではありません。条件付き最尤推定から算出されています。詳細は奥村晴彦先生のページをご参照ください。
片側検定（下側），alternative = “less”

対立仮説2 H1: オッズ比 < 1（severe グループのオッズが mild グループよりも小さい）。これは、重度群の効果ありの人数が12人以下になる確率を求める検定です。

R
fisher.test(tab, alternative = "less")
        Fisher's Exact Test for Count Data

data:  tab
p-value = 0.9935
alternative hypothesis: true odds ratio is less than 1
95 percent confidence interval:
  0.00000 29.77609
sample estimates:
odds ratio 
  5.003853

　X≦12、つまり X=12, 11, 10, ･･･, 4 となる条件付き確率を求めます。
　P(X≦12 | severe=15, mild=14, yes=18 )
　　＝P(X＝12) + P(X=11) + ・・・ + P(X=4)
　　＝0.9935

ｐ値は0.99なので帰無仮説が棄却できません。つまり、「severe グループのオッズが mild グループよりも低い」とは統計的には言えません。

両側検定, alternative = “two.sided”

対立仮説3 H1: オッズ比 ≠1（evere グループのオッズと mild グループのオッズは異なる）。severityのカテゴリー（severeとmild）とeffect（yesまたはno）の間における独立性の検定になります。

R
fisher.test(tab, alternative = "two.sided")
        Fisher's Exact Test for Count Data

data:  tab
p-value = 0.06043
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
  0.8163182 40.7244582
sample estimates:
odds ratio 
  5.003853

P=0.06 なので有意差はありません。このｐ値は後半で説明します。

次へ
123

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください

タイトルとURLをコピーしました