$ICC(1,1)：$は、一人の評価者が測定した値の信頼性や一貫性を評価します
$ICC(1,k)：$は、一人の評価者が測定した値の平均値の信頼性や一貫性を評価します
$ICC(2, 1)$では、数名の評価者が測定した値の信頼性や一貫性を評価します
$ICC(2, k)$では、数名の評価者が測定した平均値の信頼性や一貫性を評価します
$ICC(3, 1)$では、評価者を固定した場合の測定値の信頼性や一貫性を評価します（評価者間のばらつきは考慮されません）
$ICC(3, k)$では、評価者を固定した場合の測定値の平均値の信頼性や一貫性を評価します（評価者間のばらつきは考慮されません）
下記の文献のICC(3, 1)、ICC(3, k)をRでやってみます.
Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979 Mar;86(2):420-8. doi: 10.1037//0033-2909.86.2.420.
サンプルはここからです（いつもお世話になってます）
この記事を読まれる前にICC(1, 1)、ICC(2, 1)をご参照ください
例題
評価者 3名（測定回数はそれぞれ1回）、被験者 10名
ただし評価者は固定（固定効果）で、評価者間のばらつきは考慮しない
データの準備と要約
ICC(1, 1)、ICC(1, k)で使用したデータと同じファイルになります
dat <- read.csv("ICC01.csv", header=T, fileEncoding = "UTF-8")
データの確認
head(dat)
使用するパッケージ
library(irr)
library(tidyr)
library(ggplot2)
縦のデータに変換
dat2 <- tidyr::gather(
dat[,-5],
key=PT,
value=data,
-ID)
head(dat2)
変数をfactorへ変換（ここを忘れたらグラフが変わります）
dat2$PT <- as.factor(dat2$PT)
dat2$ID <- as.factor(dat2$ID)
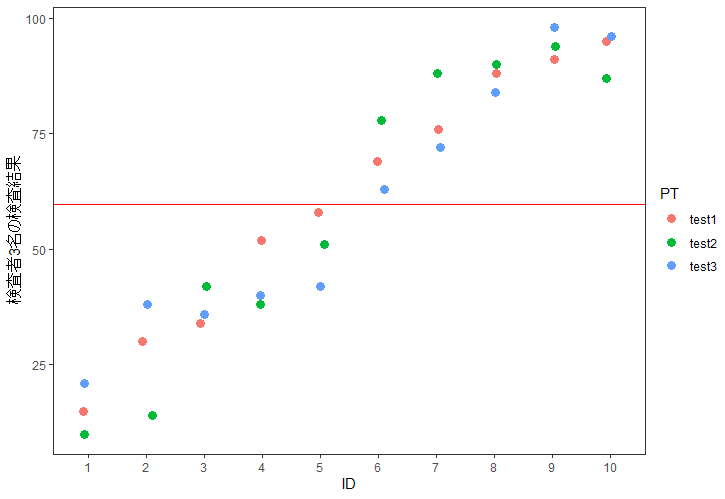
グラフでデータ構造を可視化
g1 <- ggplot2::ggplot(
dat2,
aes(x = ID, y = data)
)
g2 <- g1 + geom_jitter(
height=0, width =0.1, size = 3,
aes(colour = PT)
)
m <- mean(dat2$data)
g2 + theme_test() +
xlab("ID") + ylab("検査者3名の検査結果") +
geom_hline(aes(yintercept = m),
color = "red"
)
Rの関数でICC(3,1)をやってみましょう
Rの関数を使用してICC(3,1)を算出
モデルは2要因なのですが、特定の評価者なのでagreementではなくconsistencyを選択
つまり評価者を固定効果として考えます
irr::icc(
dat[,2:4],
model="twoway",
type="consistency",
unit="single"
)
結果のみでよければ、ここまでです
ここからは、もう少し詳しく勉強してみましょう
統計モデル
モデルは$Case2$のときと同じです
$y_{ij}=\mu+\alpha_i+\beta_j+z_{ij}$
$i=1, \dots , n \quad j=1, \dots ,k $
$\alpha_i \sim N(0, \sigma_T^2) \quad \cancel{\beta_j \sim N(0, \sigma_U^2)} \quad z_{ij} \sim N(0, \sigma_Z^2)$
患者はランダム、評価者は固定なのでミックスモデルと呼ばれます
- $\sigma_T^2$：真の分散（真の検査結果のバラツキ）
- $\beta_j$の分散=$V(\beta_j)$
- $\sigma_Z^2$：誤差による分散
＊理論はもうちょっと複雑（交互作用の効果）ですので、詳細についてはShrout(1979)をご参照ください
The Expected Mean Squares（平均平方の期待値）
患者平均平方和 (BMS: between-targets mean square) の期待値
$BMS \fallingdotseq k\sigma_T^2+\sigma_Z^2$
評価者平均平方和 (JMS: between-judges mean square)
$JMS=V(\beta_j)$
誤差平均平方和 (MSE: Mean Square Error) の期待値
$MSE \fallingdotseq \sigma_Z^2$
以上のことから
$\sigma_T^2=\dfrac{BMS-MSE}{k}$
全体の分散から$V(\beta_j)$を引いた値の推定値
$V[y_{ij}-\mu]-V(\beta_j)=\sigma_T^2+\sigma_Z^2=\dfrac{BMS-MSE}{k}+MSE$
分散に平均平方を代入してICC(3,1)を求めます
$ICC(3,1)=\dfrac{\sigma_T^2}{V[y_{ij}]-V(\beta_j)}$
$=\dfrac{\dfrac{BMS-MSE}{k}}{\dfrac{BMS-MSE}{k}+MSE}$
$=\dfrac{BMS-MSE}{BMS+(k-1)MSE}$
分散分析表
二元配置分散分析を実施してIDと残差の平均平方和からICC(3,1)を求めます
fit <- lm(data ~ ID + PT, data=dat2)
anova(fit)
分散分析表から平均平方和のみを取り出してICC(3,1)を求めてみます
BMS <- anova(fit)[1, 3] #2462.52
MSE <- anova(fit)[3, 3] #53.47
(ICC3 <- (BMS - MSE)/(BMS + (3-1)*MSE))
Rの関数iccで算出した解と同じですね
ICC(1,1)との比較
ICC(1,1)では評価者が1名なので分散分析表からは除外しています
また誤差の分散としてICC(1,1)では49.1を使用してます
ICC(3,1) の95％信頼区間
Rの関数で求めた95％信頼区間をF分布を使用した分散比の信頼区間から求めてみます
$ICC(3,1) = \dfrac{BMS-MSE}{BMS+(3-1)MSE} = \dfrac{\dfrac{BMS}{MSE}-1}{\dfrac{BMS}{MSE}+(3-1)}$
分散比（$\dfrac{BMS}{MSE}$）の95%信頼区間を代入して、ICC(3,1)の信頼区間を求めます
BMSの自由度：$n-1$
MSEの自由度：$(n-1)(k-1)$
$\dfrac{BMS}{F_{0.975}(9, 18)*MSE} \quad ～ \quad \dfrac{BMS}{F_{0.025}(9, 18)*MSE}$
BMS <- 2462.5
MSE <- 53.47
#F値
(f1 <- qf(0.025, 9, 18))
(f2 <- qf(0.975, 9, 18))
#分散比の信頼区間
(v1 <- BMS/(MSE*f2))#下限はf2を使用
(v2 <- BMS/(MSE*f1))#上限はf1を使用
#ICCの信頼区間
(v1-1)/(v1+3-1)#下限
(v2-1)/(v2+3-1)#上限
詳しくはF分布(分散比の95%信頼区間)をご参照ください
Rの関数でICC(3, k)をやってみましょう
クロンバックのα係数(Cronbach’s coefficient alpha)と同じ値になりますが、理論は異なります
3人の計測結果の平均値が対象
患者平均平方和 (between-targets mean square) の期待値
平均値をとるので一人の患者に結果が1つになります
よって
$BMS=\sigma_T^2+\sigma_E^2$
$ICC(3,3)=\dfrac{BMS-MSE}{BMS}=1-\dfrac{MSE}{BMS}$
irr::icc(
dat[,2:4],
model="twoway",
type="consistency",
unit="average"
)
BMS <- 2462.5
MSE <- 53.47
(ICC3k <- (BMS - MSE)/BMS)
ICC(3,k) の95％信頼区間の求め方
$1-\dfrac{MSE}{BMS} < ICC(3,k) < 1-\dfrac{MSE}{BMS}$
$1-\dfrac{1}{v1} < ICC(3,k) < 1-\dfrac{1}{v2}$
1-1/v1#下限
1-1/v2#上限
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください