
クロスオーバー試験の研究デザイン

クロスオーバー試験は、生物学的同等性試験や薬物動態試験で利用されています。ウォッシュアウト期間の設定がとても大切で、治療効果が無くなるのを十分に待つことになります。このデザインはリハビリテーション研究でも利用されていますが、持ち越し効果や時期効果が十分に吟味されず、間違った使い方をしているものも見られます。これらの効果はP値に直接関連してきますので、十分に注意しましょう。ここでは、折笠(2016)のなかにあるサンプルデータを使用して、同じ解析結果をRで算出してみます。FEVの値をpointとして、有意水準は5%で検定します。
2群2期のクロスオーバーデザイン、2×2 デザイン、AB/BA デザイン と呼ばれています
ランダム割り付け(s1, s2)
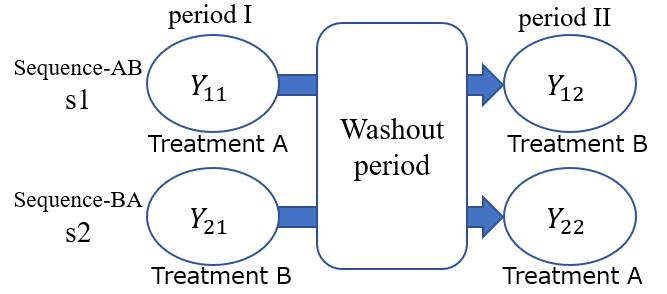
以下、 $ Y_{ij} $ という標記を使います(2×2の行列と考えてください)
$ Y_{11} =\ $s1群、I期(治療A)
$ Y_{12} =\ $s1群、II期(治療B)
$ Y_{21} =\ $s2群、I期(治療B)
$ Y_{22} =\ $s2群、II期(治療A)
データの準備と要約
使用するパッケージ(パッケージのインストール)
library(lmerTest)
library(exactRankTests)
library(dplyr)データセット crossover をdataに格納します(ファイルの読み込み)
data <- read.csv("crossover.csv", header=T, fileEncoding = "UTF-8")
head(data)
sequence: s1群(A→B)、s2群(B→A)
period: I期、II期
treatment: 治療A、治療B
point: アウトカム
IDを名義尺度に変換
data$ID <- factor(data$ID)factor() 関数は名義変数をカテゴリカル変数(因子型変数)に変換し、データのカテゴリーは「水準」として定義されます。levels() 関数で表示されるカテゴリカル変数の水準のうち、最初に表示されるカテゴリーがデフォルトで基準カテゴリー(参照カテゴリー)となり、統計モデルでの比較の基点として機能します。relevel() 関数や factor() 関数の levels 引数を使用することで、レベルの順序を指定し、基準カテゴリーを変更することが可能です。
data$period <- factor(data$period)
data$treatment <- factor(data$treatment)
levels(data$period)
levels(data$treatment)
折笠(2016)ではI-IIやA-Bの解を出力しています。参考文献に合わせて、名義変数の基準カテゴリーを変更します。
data$period <- relevel(data$period, "II")
data$treatment <- relevel(data$treatment, "B")
levels(data$period)
levels(data$treatment)
dataの要約
summary(data)> summary(data)
ID sequence period treatment point
1 : 2 Length:34 II:17 B:17 Min. :0.850
2 : 2 Class :character I :17 A:17 1st Qu.:1.285
3 : 2 Mode :character Median :1.875
4 : 2 Mean :1.902
5 : 2 3rd Qu.:2.453
6 : 2 Max. :3.350
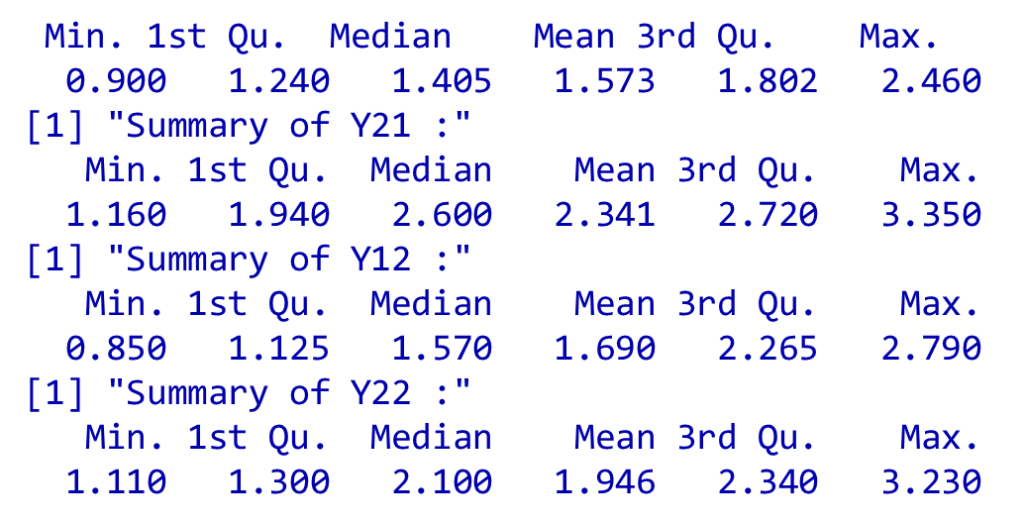
(Other):22 Y11, Y21, Y12, Y22のデータの要約
各条件に対応するデータを抽出し、サマリーを表示
variables <- c("Y11", "Y21", "Y12", "Y22")
sequences <- c("s1", "s2", "s1", "s2")
treatments <- c("A", "B", "B", "A")
for (i in seq_along(variables)) {
assign(variables[i], data[data$sequence == sequences[i] & data$treatment == treatments[i], "point"])
print(paste("Summary of", variables[i], ":"))
print(summary(get(variables[i])))
}
箱ひげ図
name <- c("Y11", "Y21", "Y12", "Y22")
boxplot(Y11, Y21, Y12, Y22, xaxt="n")
axis(side=1, at=1:4, labels=name) 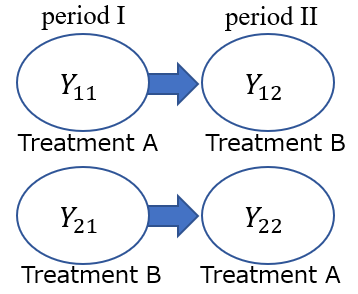
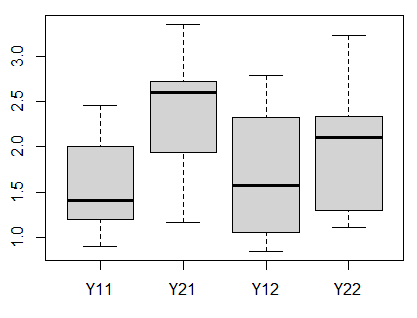
参考文献(折笠 2016)の図3の描き方
fig <- function() {
# Set up the plot with no x-axis labels yet and a pre-defined limit on x and y axes
plot(
c(0.8, 1.2, 1.8, 2.2),
c(mean(Y11), mean(Y21), mean(Y12), mean(Y22)),
xlab = "", ylab = "",
ylim = c(0.5,3.5), xlim = c(0.5, 2.5),
xaxt = "n", pch = 19, cex = 1.5 # Adjust the point character and size
)
# Add labels directly to the plot above each point
text(0.8, mean(Y11) + 0.2, "Y11", cex = 0.8, pos = 3)
text(1.2, mean(Y21) + 0.2, "Y21", cex = 0.8, pos = 3)
text(1.8, mean(Y12) + 0.2, "Y12", cex = 0.8, pos = 3)
text(2.2, mean(Y22) + 0.2, "Y22", cex = 0.8, pos = 3)
# Define period names and set the axis with these names
name <- c("Period I", "Period II")
axis(side = 1, at = c(1.1, 1.9), labels = name)
}
fig()
stm <- function(x) sd(x)/sqrt(length(x))
arrows(
c(0.8, 1.2, 1.8, 2.2),
c(
mean(Y11) - stm(Y11),
mean(Y21) - stm(Y21),
mean(Y12) - stm(Y12),
mean(Y22) - stm(Y22)
),
c(0.8, 1.2, 1.8, 2.2),
c(
mean(Y11) + stm(Y11),
mean(Y21) + stm(Y21),
mean(Y12) + stm(Y12),
mean(Y22) + stm(Y22)
),
code=3, angle=90
)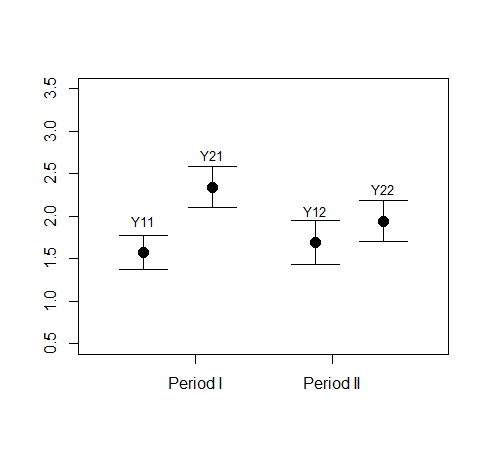
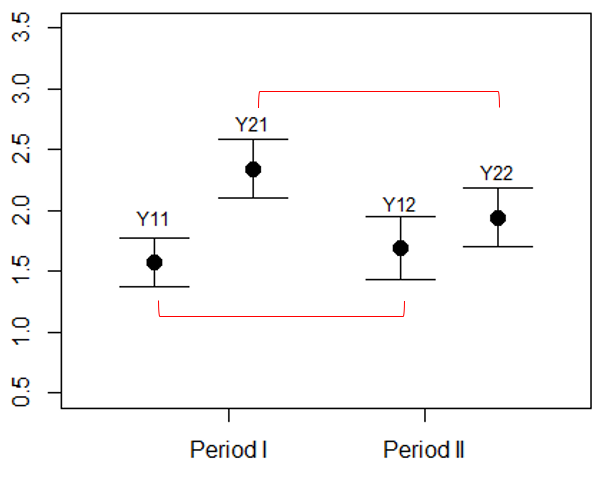
クロスオーバー試験で想定している結果
対象者を各順序群に無作為に割り付けることで、両群の治療Aと治療Bの差が同じくらいになることを想定しています。


コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください