
$ICC(1,1):$は、一人の評価者が測定した値の信頼性や一貫性を評価します
$ICC(1,k):$は、一人の評価者が測定した値の平均値の信頼性や一貫性を評価します
$ICC(2, 1)$では、数名の評価者が測定した値の信頼性や一貫性を評価します
$ICC(2, k)$では、数名の評価者が測定した平均値の信頼性や一貫性を評価します
$ICC(3, 1)$では、評価者を固定した場合の測定値の信頼性や一貫性を評価します(評価者間のばらつきは考慮されません)
$ICC(3, k)$では、評価者を固定した場合の測定値の平均値の信頼性や一貫性を評価します(評価者間のばらつきは考慮されません)

下記の文献のICC(1, 1)、ICC(1, k)をRでやってみます.
Shrout PE, Fleiss JL. Intraclass correlations: uses in assessing rater reliability. Psychol Bull. 1979 Mar;86(2):420-8. doi: 10.1037//0033-2909.86.2.420.
サンプルはここからです、いつもお世話になっております
データの準備と要約
以下のファイルを読み込んでください(ファイルの読み込み方)
dat <- read.csv("ICC01.csv", header=T, fileEncoding = "UTF-8")
ファイルにはこのような横データが入ってます
評価者 1名、被験者患 10名、測定回数 3 回
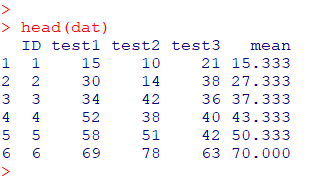
ICC(1,1)、ICC(1,k)はともに同じファイルを使用します
ICC(1, 1)とICC(1, k)の答えです
ICC(1,1)≒0.942、95%信頼区間:0.848 0.984 ICC(1,3)≒0.980、95%信頼区間:0.943 0.995

Rを使いながら、この解がどのようにして導かれたのかを解説します
使用するパッケージ
library(irr)
library(tidyr)
library(ggplot2)
縦のデータに変換
dat2 <- tidyr::gather(
dat[,-5],
key=PT,
value=data,
-ID)
head(dat2)

変数をfactorへ変換(ここを忘れたらグラフが変わります)
dat2$PT <- as.factor(dat2$PT)
dat2$ID <- as.factor(dat2$ID)
ICC(1, 1) 3回の計測結果が対象
1人の評価者が患者 ($n=10$) に対して検査を数回 ($k=3$)実施した時の信頼性を求めます
検査結果($test1, test2, test3$)の誤差が小さいと信頼性が高いと判断します
グラフでデータ構造をイメージ
g1 <- ggplot2::ggplot(
dat2,
aes(x = PT, y = data)
)
g2 <- g1 + geom_jitter(
height=0, width =0.1, size = 3,
aes(colour = ID)
)
g2 + theme_test() + xlab("") +ylab("結果")
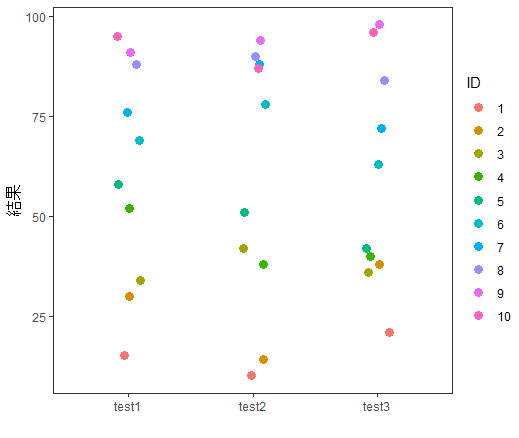

このように、IDをブロック因子とした二元配置分散分析(繰り返し測定なし)のグラフを描かれるかもしれません・・・。対応のある一元配置分散分析とも呼ばれています。でもIDを要因として考えて、以下ようなグラフをイメージしておくと理解しやすくなります。
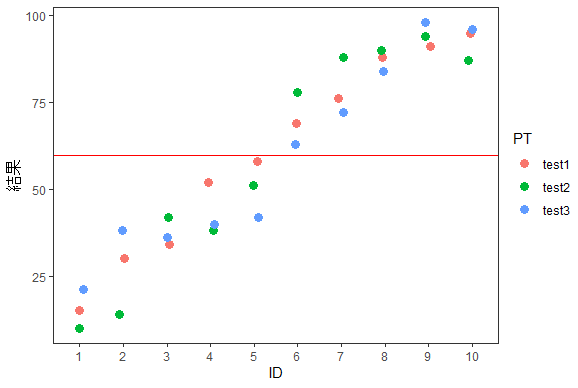
#グラフの描き方
g1 <- ggplot2::ggplot(
dat2,
aes(x = ID, y = data)
)
g2 <- g1 + geom_jitter(
height=0, width =0.1, size = 3,
aes(colour = PT)
)
m <- mean(dat2$data)
g2 + theme_test() +
xlab("ID") + ylab("結果") +
geom_hline(aes(yintercept = m),
color = "red"
)
Rの関数でICCを求める
パッケージirrのicc関数には下記のような引数が用意されています

3回計測(oneway)の一貫性(consistency)をそれぞれのデータ(single)から評価します
irr::icc(
dat[,2:4],
model="oneway",
type="consistency",
unit="single"
)
注意)横データを使っています

結果のみでよければ、ここまでです

ここからは、もう少し詳しく勉強しましょう
ICC(1, 1)の考え方
評価者の誤差(test1, test2, test3)が小さい場合、全体の分散には真の分散が影響しいてる
$\sigma^2_T$:真の分散(真の検査結果のバラツキ)
$\sigma^2_W$:誤差による分散
したがって
$ICC(1,1)$
$=\dfrac{真の分散}{真の分散 + 誤差による分散}$
$=\dfrac{\sigma^2_T}{\sigma^2_T+\sigma^2_W}$
ICC(1,1) が1に近いと3回測定した誤差の影響が小さく、「3回測定した結果の信頼性が高い」と結論付けます
統計モデル
\({y_{ij} = \mu+\alpha_i+e_{ij}}\)
$i=1, \dots , n \quad j=1, \dots ,k $
$\alpha_i \sim N(0, \sigma_T^2) \quad e_{ij} \sim N(0, \sigma_W^2)$
平均平方和よりICCを求める
$\sum\sum(y_{ij}-\bar{y})^2 = \sum\sum(\bar{y_i}-\bar{y})^2 + \sum\sum(y_{ij}-\bar{y_i})^2$
(詳細は一元配置分散分析をご参照ください)
ここでは
総平方和=患者平方和+残差平方和
とします

言葉を定義します
患者平均平方和の期待値
BMS(between-targets mean square)
残差平均平方和の期待値
WMS(whitin-target mean square)
原文通りに群間と群内という言葉で訳されていることが多いようです。ここでは理解しやすいように患者と残差とします。各患者の真の測定値が全体の分散に影響する効果、残りの誤差が全体の分散に影響する効果という意味です。
$BMS = 3*\sigma^2_T+\sigma^2_W$
$WMS = \sigma^2_W$
ここがICCで一番重要なところですが、あまりに唐突なので最下段で証明します
$ICC(1,1)$
$=\dfrac{\sigma^2_T}{\sigma^2_T+\sigma^2_W}$
$=\dfrac{BMS-WMS}{BMS+(3-1)WMS}$
分散分析表
分散分析表からBMSとWMSを当てはめてICC(1, 1)を算出してみましょう
fit <- lm(data ~ ID, data=dat2)
anova(fit)
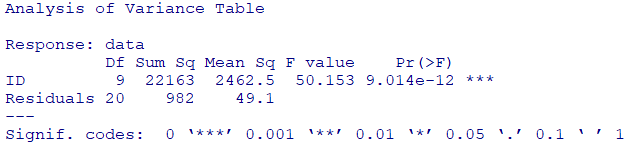
平均平方和からICCを算出します
#ICC(1,1)
BMS <- 2462.5
WMS <- 49.1
(BMS-WMS)/(BMS+(3-1)*WMS)

答えは合っています
ICC(1,1)≒0.942
ICC(1,1) の95%信頼区間
Rの関数で求めた95%信頼区間をF分布を使用した分散比の信頼区間から求めてみます
$ICC(1,1) = \dfrac{BMS-WMS}{BMS+(3-1)WMS} = \dfrac{\dfrac{BMS}{WMS}-1}{\dfrac{BMS}{WMS}+(3-1)}$
分散比($\dfrac{BMS}{WMS}$)の95%信頼区間を代入して、ICC(1,1)の信頼区間を求めます
$\dfrac{BMS}{F_{0.975}(9, 20)*WMS} \quad ~ \quad \dfrac{BMS}{F_{0.025}(9, 20)*WMS}$
BMS <- 2462.5
WMS <- 49.1
#F値
(f1 <- qf(0.025, 9, 20))
(f2 <- qf(0.975, 9, 20))
#分散比の信頼区間
(v1 <- BMS/(WMS*f2))#下限はf2を使用
(v2 <- BMS/(WMS*f1))#上限はf1を使用
#ICCの信頼区間
(v1-1)/(v1+3-1)#下限
(v2-1)/(v2+3-1)#上限

詳しくはF分布(分散比の95%信頼区間)をご参照ください
ICC(1, k) k回の計測結果の平均値が対象
$k=$3 回計測した平均値を算出
(m <- aggregate(
data ~ ID,
data=dat2,
FUN=mean
))
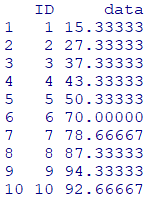
グラフにしてみましょう
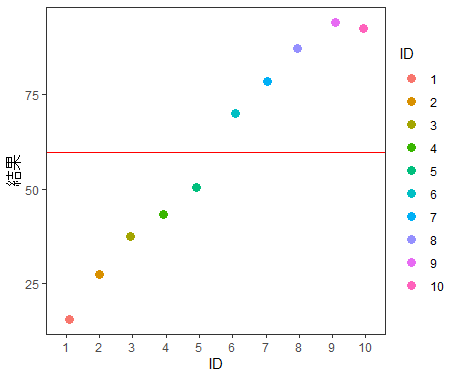
#グラフの描き方
g1 <- ggplot2::ggplot(
m,
aes(x = ID, y = data)
)
g2 <- g1 + geom_jitter(
height=0, width =0.1, size = 3,
aes(colour = ID)
)
g2 + theme_test() + xlab("ID") +ylab("結果") +
geom_hline(
aes(yintercept = mean(dat2$data)),
color = "red"
)
Rの関数でICCを求める
3回の平均なのでunitはaverageとします
irr::icc(
dat[,2:4],
model="oneway",
type="consistency",
unit="average"
)

平方和からICCを求める
$BMS \fallingdotseq \sigma^2_T+\sigma^2_W$
$WMS \fallingdotseq \sigma^2_W$
$ICC(1,3)$
$=\dfrac{\sigma^2_T}{\sigma^2_T+\sigma^2_W}$
$=\dfrac{BMS-WMS}{BMS}$
分散分析表より
#ICC(1,1)
BMS <- 2462.5
WMS <- 49.1
(BMS-WMS)/BMS
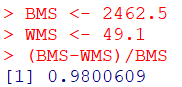
ICC(1,3)≒0.980
あってますね
ICC(1,3)の95%信頼区間
Rの関数で求めた95%信頼区間をF分布を使用した分散比の信頼区間から求めてみます
$ICC(1,3)=\dfrac{BMS-WMS}{BMS}=1-\dfrac{WMS}{BMS}$
後はICC(1,1)と同じ要領で・・・
$\dfrac{WMS}{BMS}$の信頼区間から求めます
注意)ICC(1,1)の分散比と比べると分母と分子が逆になっています
WMS <- 49.1
BMS <- 2462.5
#F値
(f1 <- qf(0.025, 20, 9))
(f2 <- qf(0.975, 20, 9))
#分散比(WMS/BMS)の信頼区間
(v1 <- WMS/(BMS*f2))#下限はf2を使用
(v2 <- WMS/(BMS*f1))#上限はf1を使用
#ICCの信頼区間(1から引くので上限と下限が逆転)
1-v2 #下限
1-v1 #上限
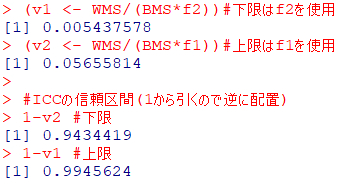
ICC(1,1)の分散比と同じ分散比を使うのであれば
$ICC(1,3)=\dfrac{BMS-WMS}{BMS}=\dfrac{\dfrac{BMS}{WMS}-1}{\dfrac{BMS}{WMS}}$
となります
平均平方和の期待値の導出
$i=1, \dotsc ,k \quad j=1, \dotsc ,n$ $\quad (k=3, \quad n=10$)
$y_{ij} = \mu+\alpha_i+e_{ij}$
条件は以下の通り (Shrout, 1979)
$\alpha_i \sim N(0, \, \sigma_T^2)$
$e_{ij} \sim N(0, \, \sigma_W^2)$
$\sum \alpha_i=0$
$\sum e_{ij}=0$
平方和の分解
$\sum\sum(y_{ij}-\bar{y})^2 = \sum\sum(\bar{y_i.}-\bar{y})^2 + \sum\sum(y_{ij}-\bar{y_i.})^2$
平方和の期待値を参照
$\sum\sum(y_{ij}-\bar{y})^2$の期待値
$E[\sum\sum(y_{ij}-\bar{y})^2]$
$=E[\sum\sum(\alpha_{i}-\bar{\alpha_{.}})^2+\sum\sum(e_{ij}-\bar{e_{..}})^2]$
$=k*(n-1)\sigma_T^2+(kn-1)\sigma_W^2$
$ \sum\sum(\bar{y_i}-\bar{y})^2$の期待値
$E[\sum\sum(\bar{y_i}-\bar{y})^2]$
$=E[\sum\sum(\alpha_{i}-\bar{\alpha_{.}})^2+\sum\sum(e_{i.}-\bar{e_{..}})^2]$
$=k*(n-1)\sigma_T^2+(n-1)\sigma_W^2$
$\sum\sum(y_{ij}-\bar{y_i})^2$の期待値
$=n(k-1)\sigma_W^2$
群平均平方和(不偏分散)の期待値
$ \dfrac{1}{n-1}\sum\sum(\bar{y_i}-\bar{y})^2$の期待値
$=k*\sigma_T^2+\sigma_W^2$


コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください