
カイ二乗分布より
カイ二乗分布に従う互いに独立な確率変数を \(Y1、Y2\) とします
\(Y1\ ~\ χ^2(k1), \ \ Y2\ ~\ χ^2(k2)\)
\(F = \dfrac{Y1/k1}{Y2/k2}\ \)は自由度(\(\ k1,k2\ \))のF-分布に従うといいます
< カイ二乗分布より >
サンプル $n=n_1, 分散=s_1^2$ の母分散を $\sigma_1^2$ とする
サンプル $n=n_2, 分散=s_2^2$ の母分散を $\sigma_2^2$ とする
(\(s_1^2\)と\(s_2^2\)は独立)
\(W1 = \sum_{i=1}^{n_1}{\dfrac{(X_i – \bar{x})^2}{σ_1^2}}=\dfrac{(n_1-1)S_1^2}{σ_1^2}\)は自由度 $ n_1-1 $ のカイ二乗分布に従う
\(W2 = \sum_{i=1}^{n_2}{\dfrac{(X_i – \bar{x})^2}{σ_2^2}}=\dfrac{(n_2-1)S_2^2}{σ_2^2}\)は自由度 $ n_2-1 $ のカイ二乗分布に従う
このような場合には
\(\dfrac{W1/(n_1-1)}{W2/(n_2-1)}=\dfrac{\dfrac{(n_1-1)S_1^2}{σ_1^2}/(n_1-1)}{\dfrac{(n_2-1)S_2^2}{σ_2^2}/(n_2-1)}=\dfrac{σ_2^2}{σ_1^2}\dfrac{S_1^2}{S_2^2}\)
は、自由度 $(n_1-1, n_2-1)$ のF分布に従い、 $F(n_1-1, n_2-1)$ と表現します
等分散性の検定
サンプル $n=n_1, 分散=s_1^2$ の母分散を $\sigma_1^2$ とする
サンプル $n=n_2, 分散=s_2^2$ の母分散を $\sigma_2^2$ とする
- 帰無仮説:$\sigma_1^2=\sigma_2^2$
- 対立仮説:$\sigma_1^2\neq\sigma_2^2$
サンプルの分散比の分布はF分布となる
\(F=\dfrac{s_1^2}{s_2^2} \sim F(n_1-1,n_2-1)\)
このことを利用して以下のようなことを考えることができます
例題 血圧測定した結果、A群51名の分散10mmHg, B群31名の分散5mmHgであった A群とB群の母分散は等しいと言えるか、有意水準2.5%で片側検定せよ 帰無仮説:母分散は等しい 対立仮説:A群の母分散>B群の母分散
$n_1=51$
$s_1^2=10$
$n_2=31$
$s_2^2=5$
A群の分散10mmHg, B群の分散5mmHgなので、母分散が等しいと仮定した場合には
$ \dfrac{s_1^2}{s_2^2}=\dfrac{10}{5} $、つまり$ F=2 $となる
したがって$ P(F>2) $となる確率が$ 0.025 $以下になれば帰無仮説が棄却される
$ \dfrac{s_1^2}{s_2^2} \sim F(51-1, 31-1) $ よりp値を求める
pf(2, 51-1, 31-1, lower.tail=F)
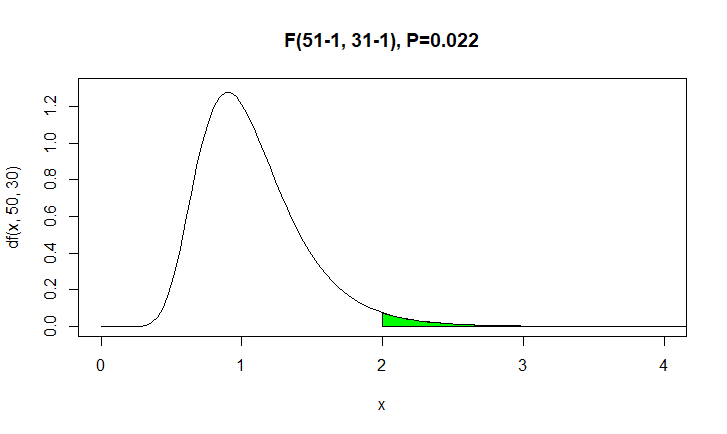
$F>2$ の確率が $P=0.022$ なので、帰無仮説は棄却される $(p<0.025)$
つまり2群の母分散は異なることが証明されました
curve(
df(x, 50, 30),
type="l",
ylim=c(0, 1.3),
xlim=c(0, 4),
main="F(51-1, 31-1), P=0.022"
)
x <- qf(
pf(2, 50, 30, lower.tail=F),
50, 30,
lower.tail = F
)
x1 <- seq(x, 5,length=100)
y <- df(x1, 50, 30)
polygon(
c(x1, rev(x1)),
c(rep(0, length(x1)), rev(y)),
col="green"
)
$P=0.025$ と重ねてみましょう
curve(
df(x, 50, 30),
ylim=c(0, 1.3), xlim=c(0, 4),
type="l",
main="F(51-1, 31-1),P=0.025(ピンク)"
)
x <- qf(0.025, 50, 30, lower.tail=F)
x1 <- seq(x, 5,length=100)
y <- df(x1, 50, 30)
polygon(
c(x1, rev(x1)),
c(rep(0, length(x1)),
rev(y)),
col="pink"
)
x <- qf(pf(2, 50, 30, lower.tail=F), 50, 30, lower.tail=F)
x1 <- seq(x, 5,length=100)
y <- df(x1, 50, 30)
polygon(
c(x1, rev(x1)),
c(rep(0, length(x1)), rev(y)),
col="green"
)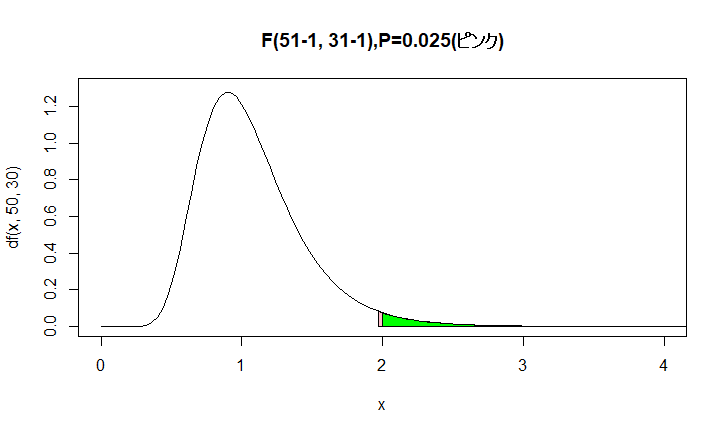
緑の領域がわずかにピンクより少なくですね
この図からも $P<0.025$ ということが分かります
★ 上側確率
\(F_α(n_1-1, n_2-1)\):上側確率が \(α\)となる値を上側確率\(100α%\)のパーセント点という
例)パーセント点 \(F_{0.025}(50, 30)\)
qf(0.025, 50, 30, lower.tail = F)
curve(
df(x, 50, 30),
ylim=c(0,1.3), xlim=c(0,4),
type="l",
main="F(51-1, 31-1)"
)
x <- qf(0.025, 50, 30, lower.tail = F)
x1 <- seq(x, 5,length=100)
y <- df(x1, 50, 30)
polygon(
c(x1, rev(x1)),
c(rep(0, length(x1)), rev(y)),
col="pink"
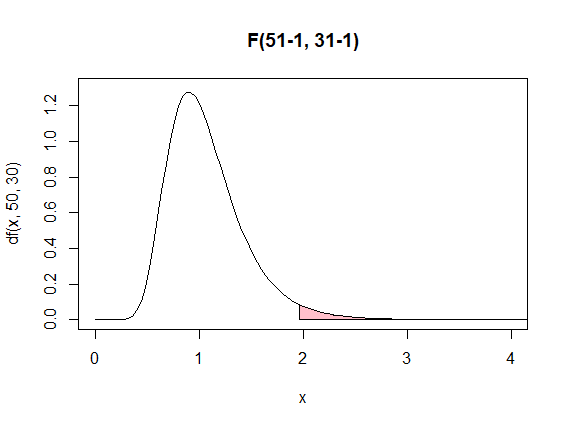
)ピンクの部分がP値=0.025です
有意水準0.025を仮定した等分散性の検定の場合、ピンク色の部分が下図より小さくなれば2群の母集団の等分散が仮定できなくなります
F分布の性質
詳しいことは下の二項分布とF分布の関係をご参照ください
$F$が $F(n_1-1, n_2-1)$ に従う場合、$\dfrac{1}{F}$ は、$F(n_2-1, n_1-1)$ に従う
ゆえに $F_α(n_1-1, n_2-1)=\dfrac{1}{F_{1-α}(n_2-1, n_1-1)}$
par(mfrow=c(1,2))
curve(
df(x, 20, 10),
ylim=c(0, 1), xlim=c(0, 5),
xlab="", ylab="",
type="l",
main="F(20-1, 10-1)"
)
x <- qf(0.025, 20, 10) #0.360533
x1 <- seq(0, x, length = 100)
y <- df(x1, 20, 10)
polygon(
c(x1, rev(x1)),
c(rep(0, length(x1)),
rev(y)), col="pink"
)
curve(
df(x, 10, 20),
type = "l",
ylim = c(0, 1), xlim = c(0, 5),
xlab="",
ylab="",
main="F(10-1, 20-1)"
)
x <- qf(0.975, 10, 20) #2.773671
x1 <- seq(x, 5, length = 100)
y <- df(x1, 10, 20)
polygon(
c(x1,rev(x1)),
c(rep(0,length(x1)), rev(y)),
col="pink"
)
par(mfrow=c(1,1)) 左:\(F_{0.025}(20, 10)=0.360533\)、右:\(F_{0.095}(10, 20)=2.773671\)
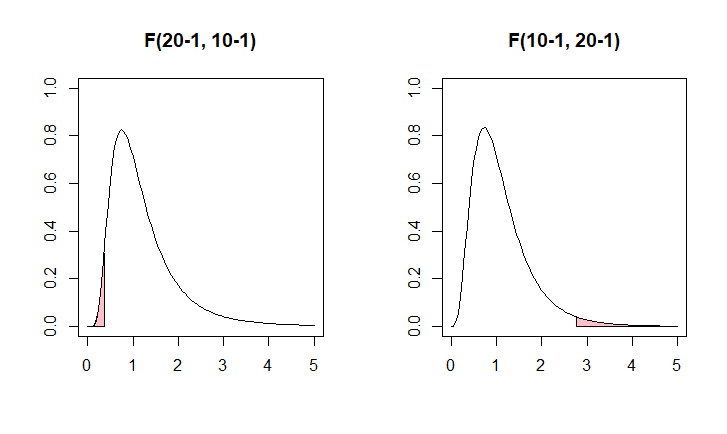
\(F_{0.025}(20,10) = \dfrac{1}{F_{1-0.025}(10,20)}\)
\(0.360533 = \dfrac{1}{2.773671}\)
分散比の95%信頼区間
$\dfrac{x1}{x2}$の分散比の信頼区間を求めます
x1 <- c(6, 4, 5, 1, 9, 9, 3, 10)
x2 <- c(10, 12, 15, 13, 11, 9)
var.test(x1, x2)
95%信頼区間 0.3255279 ~ 11.7906623 の求め方
\(0.025\%点 \leq \dfrac{s_1^2}{\sigma_1^2}/\dfrac{s_2^2}{\sigma_2^2} \leq 0.975\%点\)
\(0.025\%点*\dfrac{s_2^2}{s_1^2} \leq \dfrac{\sigma_2^2}{\sigma_1^2} \leq 0.975\%点*\dfrac{s_2^2}{s_1^2}\)
$\dfrac{s_1^2}{0.975\%点*s_2^2} \leq \dfrac{\sigma_1^2}{\sigma_2^2} \leq \dfrac{s_1^2}{0.025\%点*s_2^2}$
#各群の不偏分散
(v1 <- var(x1))
(v2 <- var(x2))
#対象となる分散比
v1/v2
#0.025%点と97.5%点
(f1 <- qf(0.025, 7, 5))
(f2 <- qf(0.975, 7, 5))
#信頼区間
v1/(v2*f2)#下限はf2
v1/(v2*f1)#上限はf1
確率関数、期待値、分散
★ 確率密度関数
ベータ分布 \(B(m/2, n/2)\)
\(\displaystyle f(x; m, n)=\frac{m^{m/2}n^{n/2}}{B(m/2, \ n/2)}\frac{x^{\frac{m}{2}-1}}{(mx+n)^{\frac{p+q}{2}}}\) \(\ \ \ (x>0)\)
ベータ分布とガンマ分布の関係より
\(Γ(α)Γ(β)=Γ(α+β)B(α,\ β)\)
\(\displaystyle B(α,\ β)=\frac{Γ(α)Γ(β)}{Γ(α+β)}\)
これをはてはめて以下のようにも書けます
\(\displaystyle f(x; m, n)=\frac{Γ(\frac{m+n}{2})m^{m/2}n^{n/2}}{Γ(m/2)Γ(n/2)}\frac{x^{\frac{m}{2}-1}}{(mx+n)^{\frac{p+q}{2}}}\) \(\ \ \ (x>0)\)
★ 期待値
\(\displaystyle E[X]=\frac{n}{n-2}\) ただし\(n>2\)のときのみ
★ 分散
\(\displaystyle V[X]=2(\frac{n}{n-2})^2\frac{m+n-2}{m(n-4)}\) ただし\(n>4\)のときのみ
二項分布とF分布の関係
\(X~B(n,π)\)のとき、以下の式が成り立つ
上側検定の場合
P値=\(\displaystyle P(X \geq x)=P(F(m, n) \geq \frac{m(1-π)}{nπ}), \ \ \ m=2(n-x+1), n=2x\)
下側検定の場合
P値=\(\displaystyle P(X \leq x)=P(F(m, n) \geq \frac{nπ}{m(1-π)}), \ \ \ m=2(x+1), n=2(n-x)\)
証明はウサギさんの統計学サロンで

