例題 リハビリを受けている入院中の患者に対してリハビリに関する満足度調査を実施した。1週間に割り当てられた単位数をもとにランダムにインタビューした。「満足」と回答する割合と1週間のリハビリ単位数には関係があるのでしょうか？
僕が作った架空のデータで練習しましょう。単位数は5単位毎に設定してます。例題の内容や結果については色々とご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。
データの準備と要約
データセット log01 をdat に読み込みます（ファイルの読み込み方）
dat <- read.csv("log01.csv", header=T, fileEncoding = "UTF-8")
データの確認
dat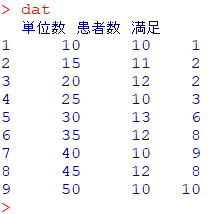
（満足＝満足と回答した人数）
y軸を「満足と回答する確率」、ｘ軸を「単位数」とします
g1 <- function(){
plot(満足/患者数~単位数, data=dat, ylab="満足と回答する確率")
}
g1()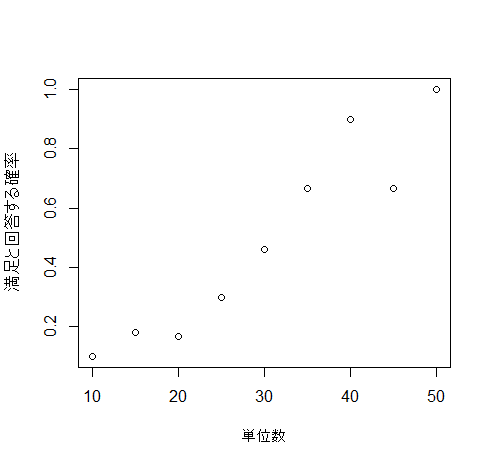
そのまま単回帰分析を実行して、回帰直線を挿入してみます
reg <- lm(満足/患者数~単位数, data=dat)
g1()
abline(reg)
#lines(range(dat$単位数), reg$coef[1] + reg$coef[2]*range(dat$単位数)) と同じ直線
詳細は単回帰分析をご参照ください
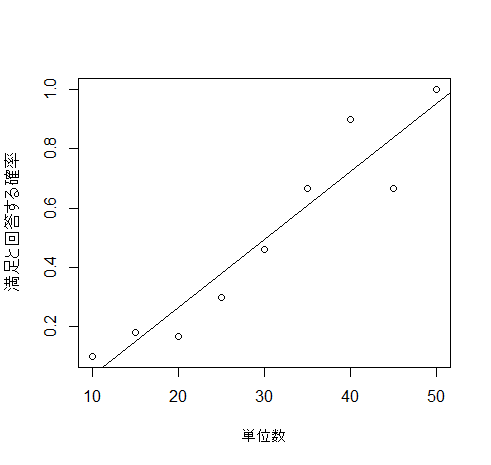
患者が満足と答える確率は0～1となるべきなのですが、回帰直線では0と1を突き抜けてしまいます
この直線では満足度とリハビリ単位数の関係が十分に説明できません
Rを使用したロジスティック回帰分析
目的変数が連続変数（誤差が等分散正規分布）ではないので、一般化線形モデルと呼ばれています。特に目的変数が0または1の二値の場合は、二項分布に基づくロジスティック回帰モデルを使用します。Rの関数は 一般線形モデル＝lm(linear model) 、一般化線形モデル＝ glm(generalized linear model) となります・・・少しややこしいですね。
Rでは以下のように書きます
fit <- glm(
cbind(満足, 患者数-満足) ~ 単位数,
family=binomial,
data=dat
)
結果のまえに、この式のcbindの中を確認してみましょう
cbind(dat$満足, dat$患者数-dat$満足)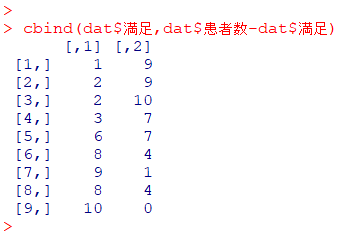
１単位から9単位までの満足と非満足の数が出力されました
$\dfrac{1列目}{2列目}$ がオッズ比になっているのが分かります
この表から感度・特異度が算出されるので、ROC曲線を描くことができることも納得できますね
結果
summary(fit)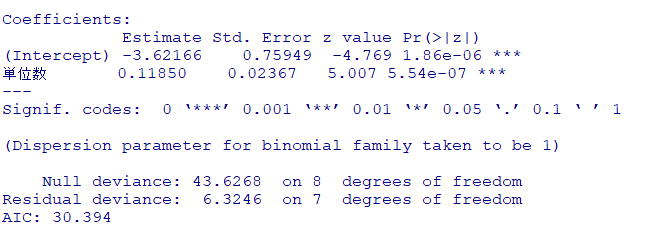
ロジスティック回帰分析の結果、リハ単位数が増えると「満足」と回答する確率 $P$ が有意に上昇することが分かりました
リハビリ単位数が1週間に5単位上がると、満足と回答する割合のオッズが有意に$e^{0.1185}\fallingdotseq1.13$倍に上がる（13%アップ）ことを意味しています（理由は「結果の解釈」に記載してます）
結果のみでよければ、ここまででOKです
ここからはもう少し詳しく学習しましょう
ロジット変換、ロジスティック変換（logistic transformation)
ロジット変換とは、確率 $\pi$ を $log\dfrac{\pi}{1-\pi}$ へ変換することです
この変換により、$0<\pi<1$ に対して、 $-\infty<log\dfrac{\pi}{1-\pi}<\infty$ となります
ロジット変換は、説明変数がどんな値をとっても予測値が0から1に収まるように目的変数を変換する方法です。0または1を目的変数とする統計的推測に柔軟性を持たせた方法と言えます。
① 満足と答える確率 $P$ のオッズを求めます
リハビリを1週間に$x_i$単位 受けた患者が満足と答える確率 $P$ のオッズを満足度オッズとします
満足度オッズ=$\dfrac{満足と答える確率}{1-満足と答える確率}=\dfrac{P(x_i)}{1-P(x_i)} \qquad (x_iはリハ単位数)$
② 満足度オッズを対数変換します（ロジット変換）
満足度オッズ $\dfrac{P(x_i)}{1-P(x_i)}$ の対数をとります（$0<P(x_i)<1$）
$logit(P)=log(\dfrac{P(x_i)}{1-P(x_i)})$
ロジスティック変換をする理由
$0<P<1$ の範囲で $-\infty<logit(P)<\infty$ となり、線形回帰（ $logit(P)=\beta_0+\beta_1x_i$ ）に置き換えることで、リハビリ単位数 $x_i$ がどのような値でも$0<P(x_i)<1$ の範囲に収まることになります
これで、単回帰のように予測式が0または1を突き抜けることはありません
ｘ軸が確率、y軸が $logit(P)$ のグラフからはシグモイド曲線になることが確認できます
y <- function(P){
return(log(P/(1-P)))
}
plot(y, xlab ="P", ylab = "logit(P)")
abline(0,0)
このシグモイド曲線を利用することで、リハビリを $x_i$時間 受けた患者が満足と答える確率 $P(x_i)$ を予測できそうですね！
ロジスティック回帰モデル
$logit(P) = \beta_0+\beta_1x_i$
＊ここでは、推定したいパラメタを $\beta_i$、推定の結果得られた係数を $b_i$ として区別します
$x_i$ がリハビリ単位数とすると、このモデルからパラメタを推定することで
$logit(\hat{P})=b_0+b_1*x_i$
のような予測式を立てることができます（$\hat{P}$は予測確率です）
family = binomial
今回の例では各単位ごとに上限があるカウントデータとなります。このような場合は二項分布を使用します（family = binomial）。上限がない場合にはポアソン分布を利用するとになります（family = poisson）。
link=”logit”
目的変数を $ax + b$ のような一次方程式（多変数もあり）に対応させるための関数をリンク関数と呼びます。今回の場合はロジット変換したので、リンク関数は ロジットリンク関数 $log(\dfrac{P}{1-P})$ です。Rでは link=”logit” と指定します。二項分布のデフォルトになっていますが、正確には以下のように書きます（もちろん答えは同じです）。
fit <- glm(
cbind(満足, 患者数-満足) ~ 単位数,
family=binomial (link="logit"),
data=dat
)
cbind(満足, 患者数-満足)の2列を link=”logit” でロジット変換して、確率分布は family = binomial で二項分布を指定して尤度を求める・・・という式になります
モデル
$logit(P) =log(\dfrac{P}{1-P})=\beta_0 + \beta_1x_i$
$P=$満足と回答する確率, $x_i=$単位数
$P$ について解くと以下のようになります
$P=\dfrac{e^{\beta_0 + \beta_1x_i}}{1 + e^{\beta_0 + \beta_1x_i}}$ （変数 $x_i$ が多い場合、傾向スコアとして使用される値です）
グラフ
ロジスティック回帰の結果から $b_0$ と $b_1$ が推定されたので、上記の式に当てはめてｘ軸を「リハビリ単位数」、ｙ軸を「満足と回答する確率$\hat{P}$」とした予測曲線を描くことができます
#x軸の範囲
x <- seq(0, 60)
#切片
b0 <- coef(fit)[1]
#回帰係数
b1 <- coef(fit)[2]
#推定された確率
y <- exp(b0 + b1*x)/(1+exp(b0 + b1*x))
#満足と答える確率の予測曲線（実践）
plot(
x, y, type="l",
xlim=c(0, 60), ylim=c(0,1),
xlab="リハビリ単位数", ylab="満足と回答する確率"
)
#図を重ねる
par(new=T)
#満足と答えた確率の実測値（ドット）
plot(
満足/患者数~単位数,
xlim=c(0, 60), ylim=c(0,1),
xlab="", ylab="",
data=dat
)
注意）ドットは実測値から求めた確率、実線は予測確率
結果の解釈
再掲
1週間のリハビリ単位数が5単位上がると、満足と回答する割合のオッズが$e^{0.1185}\fallingdotseq1.13$倍になることを意味しています
この結果の解釈はモデルから証明できます
$logit(P|x_i) =log(\dfrac{P_{x_i}}{1-P_{x_i}})=\beta_0 + \beta_1x_i$
$logit(P|x_i+1) =log(\dfrac{P_{x_i+1}}{1-P_{x_i+1}})=\beta_0 + \beta_1(x_i+1)$
$logit(P|x_i+1)-logit(P|x_i) = log(\dfrac{\dfrac{P_{x_i+1}}{1-P_{x_i+1}}}{\dfrac{P_{x_i}}{1-P_{x_i}}}) =\beta_1$
以下のようにも書けます
$\dfrac{\dfrac{P_{x_i+1}}{1-P_{x_i+1}}}{\dfrac{P_{x_i}}{1-P_{x_i}}}=\dfrac{e^{\beta_0 + \beta_1x_i}}{e^{\beta_0 + \beta_1(x_i+1)}}=e^{\beta_1}$
したがって、$ｘ_i$ が1増加するとオッズ（$\dfrac{P_{x_i}}{1-P_{x_i}}$） が $e^{\beta_1}$ 倍になることが理解できます
十分理解したうえで、結果を考察するようにしましょう！
パラメタ推定（対数尤度による最尤推定法）
$b_0$ と $b_1$ をどのようにして推定したのか？
最尤推定法とは、確率分布を前提にして尤度関数と最尤推定量を求める方法のことです。なんだか難しそうですが、尤度、尤度関数、最尤推定量などを例題に沿って説明してみます。
$ P_i=\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}} $ $(i=1,2,\dotsc,9)$
$P_i$ には $\beta_0$ と $\beta_1$ が含まれているので、ここでは推定するパラメタを $P$ として進めます
$ x_i=$単位数に$(i=1,2,\dotsc,9)$を当てはめることで、9つの $P_i$ を仮定します
例) $i=2$の場合 $P_2=\dfrac{e^{\beta_0+\beta_1*15}}{1 + e^{\beta_0+\beta_1*15}}$
$\beta_0, \beta_1$ は未定のまま、パラメタ $P_i $ を仮定して確率分布関数（二項分布）に挿入して尤度を求めます
尤度 $= _{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i}$
このように現象からパラメタを “仮定” して求めた確率を尤度といいます
この尤度が最大になるときは尤も最もらしいパラメタ推定が行われた・・・ということで、このとき推定されたパラメタを最尤推定量といいます（最終的に算出されたパラメタ推定値を最尤推定値といいます）
例題では9つデータ（単位数 $x_i : 10, 15, …, 50$）からなり、以下の尤度関数から尤度を求めることができます
$L_{\theta}=P_1*P_2* \dotsi *P_9$
尤度関数はパラメタ $P_i$ の関数となります（つまり尤度関数は $\beta_0,$ と $\beta_1$ の関数になります）
尤度関数
満足の確率 $P_i=\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}}$
満足ではない確率 $1-P_i=1-\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}}$
尤度関数 $L_{\theta}$
$L_{\theta}=\prod_{i=1}^{n}(\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}})^{y_i}*(1-\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}})^{n_i-y_i}$ ($n=9, n_i=$患者数, $y_i =$ 満足)
二項分布ですので以下のように書き換えることができます
$L_{\theta}=\prod_{i=1}^{n} (_{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i})$
パラメタである$P_i (\beta_0, \beta_1)$を求めるのですが、掛け算なので効率的ではありません。通常は以下のように対数変換して「足し算」に変換して求めます。
対数尤度関数
尤度$L_{\theta}$ の対数を $l_{\theta}$ （対数尤度）とします
$l_{\theta}=log(\prod_{i=1}^{n} (_{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i}))$
これを解くと以下のようになります ($_{n_i}C_{y_i}$ の部分は $Const$)
$l_{\theta}=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))+Const.$
この対数尤度が最大になるような$\beta_0$ と $\beta_1$ を推定します（対数尤度による最尤推定法）
$\beta_0$ と $\beta_1$ で偏微分した連立方程式を解きます
この方程式を解くためには、ニュートン-ラフソン法（Newton-Raphson法）などを用います
対数尤度はモデルのあてはまりの良さ（尤もらしさ）を示す指標となります。
Wald検定
最尤推定法より求めたパラメタの推定値$b_i$（$b_0, b_1$）が、パラメタの真の値($B_0$とする) と同じかどうかの検定
帰無仮説：$B_0=b_i$（通常は$B_0=0$を仮定する）
対立仮説：$B_0 \neq b_i$（通常は$B_0=0$を仮定する）
再掲(fit)
Estimate：最尤推定法より求めたパラメタ推定値 $b_0, b_1$（この推定値を検定します）
Std.Error：標準誤差
z value：Z検定量（推定値÷標準誤差）
Rのロジスティック回帰の係数の検定では、二項分布に基づき正規分布による検定（詳細は二項分布のページをご参照ください）でP値を求めています
Wald検定：z valueを二乗した値（Wald統計量, Wald–squareと呼ばれる）が自由度1のカイ二乗分布に従うことを利用した検定
Wald統計量$=(\dfrac{b_i-\beta_p}{SE})^2$
正規分布による検定と同じp値になるので、Rが算出しているようなZ値をWald統計量と書いていることもあるようです。下記に示す通りp値は同じ値になります。
例）単位数の係数の推定値$b_1$の検定
est <- summary(fit)$coef[2,1]
se <- summary(fit)$coef[2,2]
#正規分布による検定
pnorm(est / se, lower.tail=F)*2
#カイ二乗分布による検定
pchisq((est / se)^2, 1, lower.tail=F)
*よく使う関数をご参照ください
モデルの適合度判定
対数尤度：$l_{\theta}=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))$
逸脱度（deviance）：$deviance = -2 \, × $ 対数尤度
対数尤度から求める逸脱度（deviance）は、モデルの当てはまりの「悪さ」を意味しています。Rは各モデルのdevianceの差を算出します。最も当てはまりのよいFull modelと最も当てはまりの悪いNull modelとの差をNull deviance、回帰分析モデルとフルモデルとの差をResidual devianceといいます。
最大逸脱度（$D_{max}$）= Null modelの逸脱度 (Null devianceではありません)
➡ Null model : 説明変数のないモデル＝切片モデル：最も当てはまりの悪いモデル
最小逸脱度（$D_{min}$）= Full modelの逸脱度
➡ Full model：全てのデータを二項分布に当てはめたモデル
Rでは Null deviance と Residual deviance が算出されます
Null model
#Null modelでのロジスティック回帰
null <- glm(
cbind(満足, 患者数-満足) ~ 1,
family = binomial,
data = dat
)
print(null)
回帰分析によるモデル
再掲
fit <- glm(
cbind(満足, 患者数-満足) ~ 単位数,
family=binomial,
data=dat
)
summary(fit)
Deviance(逸脱度)の求め方
RのlogLik関数で各モデルによる最大対数尤度が算出されます（便利ですね・・・）
#最大逸脱度（Null modelの逸脱度）
-2*logLik(null)
#回帰分析モデルの逸脱度
-2*logLik(fit)
#最小逸脱度（Full modelの逸脱度）
-2*sum(log(dbinom(dat$満足, dat$患者数, dat$満足/dat$患者数)))
★最小逸脱度（Full modelの逸脱度）の求め方
Full modelの対数尤度：$lmin=\log(\sum (P_i^{y_i}(1-P_i)^{n_i-y_i})))$
$\beta_0, \beta_1$ を推定するのではなく、$P_i$には実測値から得らた確率 ($\dfrac{満足}{患者数}$) を直接挿入します
最小逸脱度$=-2*lmin$
尤度比検定（ｶｲ二乗検定による方法）
Null modelと回帰分析モデルの最大対数尤度の差に-2を掛けた値がｶｲ二乗分布に近似することを利用した検定
帰無仮説：Null model
対立仮説：回帰分析によるモデル
尤度比検定の統計量
-2*(logLik(null) - logLik(fit))
P値
pchisq(-2*(logLik(null) - logLik(fit)), 1, lower.tail=F)
下記のように分散分析からも求めることができます
anova(null, fit, test = "Chisq")
Model1 : Null model
Model2 : 回帰分析によるモデル
検定結果は、p<0.001となり回帰分析モデルが真のモデルであるという結果になりました
帰無仮説は棄却され対立仮説の回帰モデルによる推定が支持されることになります
★サンプルサイズが小さい場合には、パラメトリックブートストラップ法により求めます（参考文献にはサンプルサイズが100くらいであればｶｲ二乗分布近位は正確なP値が得られないと書かれています）
参考文献：久保拓弥. (2012). データ解析のための統計モデリング入門 (Vol. 267). 岩波書店.
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください