単回帰分析

データの準備と要約
Rで単回帰分析
- p値の意味

データの準備と要約

僕が作った架空のデータで練習しましょう。結果についてはご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。

例題
PT単位数がFIM運動項目（mFIM）に与える影響について検証します
対象：9名の脳卒中患者
目的変数：FIM差 = PT後mFIM - PT前mFIM
説明変数：理学療法実施単位数（PT単位数）

データセットlm01をdatに格納します（ファイルの読み込み）

lm01 データのダウンロード

dat <- read.csv("lm01.csv", header=T, fileEncoding = "UTF-8")
#View(dat)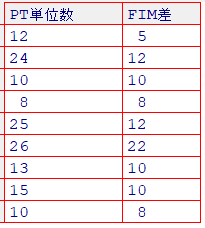

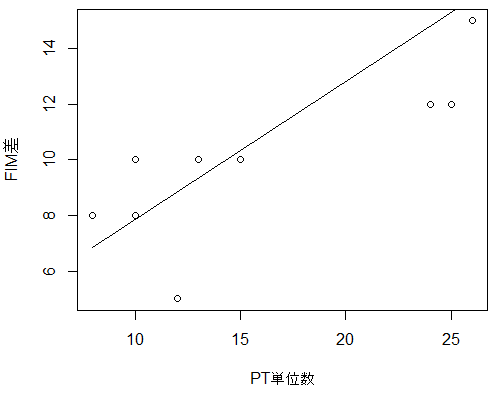
散布図

plot(FIM差~PT単位数, data=dat)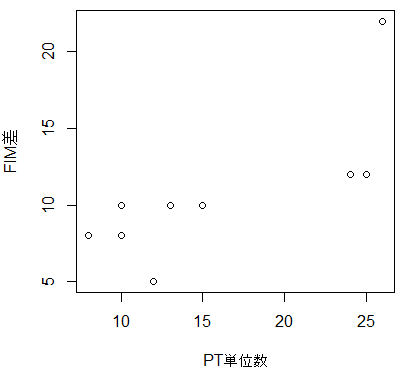

Rで単回帰分析

lmはlinear model（linear regression model）の略です

fit <- lm(FIM差~PT単位数, data=dat)
print(fit)

これで以下のような回帰式が求められます

$y=2.86+0.50x$

切片と傾きは、有意な数値なのか有意水準5％で検定してみましょう

summary(fit)

傾きのｐ値（0.0199）は0.05未満なので有意です

PT単位数が1単位増えるとFIM差は約0.5増加することが予測できました

F値（9.012）が出力されています

結果のみが必要な場合は、ここまで大丈夫です

ここからはもう少し詳しくなります

分散分析

分散分析を実行することで、単回帰分析の結果に記載されているF値（9.012）が算出されます

anova(fit)

分散分析表

詳細は分散分析のページをご参照ください

回帰分析表と分散分析表について、重回帰分析のページに記載してます

グラフ

散布図に回帰直線を加えてみます

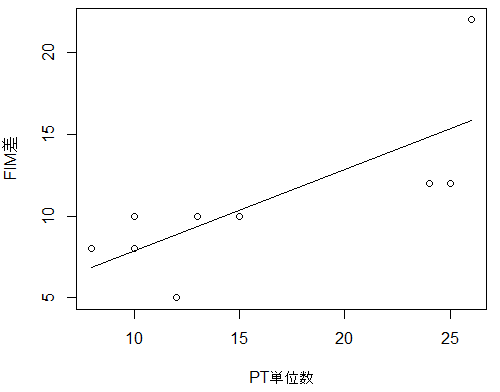
グラフの描き方

plot(FIM差~PT単位数, data=dat)
x0 <- range(dat$PT単位数) #x軸の範囲
b0 <- fit$coef[1] #切片
b1 <- fit$coef[2] #傾き
lines(x0, b0 + b1*x0) #回帰直線

p値の意味

おそらくFIM差22が１名いるので、切片が十分に予測できないようですね

試しに6行目のFIM差22を15に置き換えた以下のデータでやってみましょう

注意）あくまでも統計学の勉強のためのデータ操作です

lm02 サンプルのダウンロード

dat2にデータを格納します

dat2 <- read.csv("lm02.csv", header=T, fileEncoding = "UTF-8")
#View(dat2)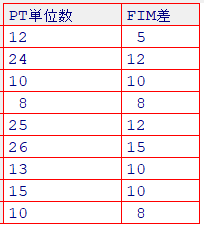

fit2 <- lm(FIM差~PT単位数, data=dat2)
summary(fit2)

予測通りにこのデータだと切片も有意になりました（p値=0.017）

#グラフの描き方
plot(FIM差~PT単位数, data=dat2)
x0 <- range(dat2$PT単位数) #x軸の範囲
b0 <- fit$coef[1] #切片
b1 <- fit$coef[2] #傾き
lines(x0, b0 + b1*x0)

ほとんどのリハビリテーション研究では、複数の因子が結果に影響を与えるため、単回帰分析では結果を十分に考察することが困難です。特に、原因から結果を予測する場合、複数の交絡する要因が存在する可能性があります。これらの因子を統計学では交絡因子（confounder、confounding factor）と呼び、独立変数と目的変数の両方に影響を与えることで結果の解釈を歪める可能性があります。交絡因子の影響を調整するためには、単変量解析だけでなく、層別解析、傾向スコア、多変量解析などの手法を用いた十分な吟味が必要です。

繰り返しになりますが、ここでは交絡因子は無視して「PT単位数でFIM差を予測する」という、あり得ない仮定で進めていますのでご注意ください。

外挿に注意

ただし、今回取得したデータの範囲外（外挿：Extrapolation）の予測は、誤った予測値になる可能性があるので注意が必要です