一元配置分散分析

1ページ　2ページ　3ページ

データの準備と要約

例題
歩行が自立している高齢者のバランストレーニングの効果を確認するために、30名を対象に床反力計を使用して足圧中心(COP)の総軌跡長を30秒間評価した。年齢別に差があるか有意水準5％で検定してみましょう。

僕が作った架空のデータで練習しましょう。結果についてはご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。

使用するパッケージ

library(tidyverse)
library(multcomp)

以下のファイルを読み込んでください（ファイルの読み込み方）

data <- read.csv("anova-01.csv", header=T, fileEncoding = "UTF-8")

縦のデータセットです

head(data)

> head(data)
  ID data   age
1  1 1129 65-70
2  2 1009 65-70
3  3 1289 65-70
4  4 1052 65-70
5  5  995 65-70
6  6 1288 65-70

IDとageはカテゴリー変数（因子型変数）に変更しす。名義変数（カテゴリカル変数）を factor() 関数を使用して因子型変数に変換することで、そのデータの値（カテゴリー）は「水準」（levels）として定義されます。

data <- data %>% mutate(
  ID = factor(ID), 
  age = factor(age)
)
levels(data$age)

> levels(data$age)
[1] "65-70" "70-75" "75-80"

グラフ

p <- ggplot(data, aes(x = age, y = data)) +
  geom_jitter(width = 0.05, size = 3, alpha = 0.6) + 
  labs(x = "Age", y = "Data", title = "Data Distribution by Age Group") +
  theme_minimal()
print(p)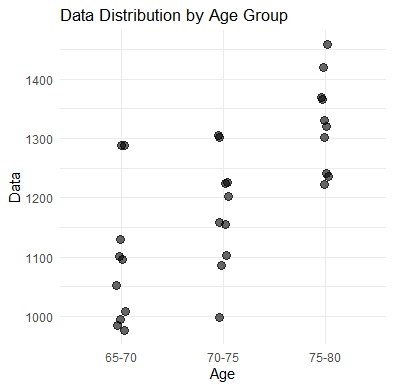

各グループの要約（’age’ 別に’data’の平均値、標準偏差、最小値、最大値を計算し、小数点第2位で丸める）

result <- aggregate(
  data ~ age, data = data, 
  FUN = function(x) {
    c(mean = round(mean(x, na.rm = TRUE), 2), 
    sd = round(sd(x, na.rm = TRUE), 2), 
    min = round(min(x, na.rm = TRUE), 2), 
    max = round(max(x, na.rm = TRUE), 2))
})

print(result)

> print(result)
    age data.mean data.sd data.min data.max
1 65-70   1092.00  116.07   977.00  1289.00
2 70-75   1175.90   96.73   998.00  1305.00
3 75-80   1326.00   79.44  1222.00  1458.00

回帰分析と分散分析

回帰分析

分散分析表の前に単回帰分析を実施します。ただしageは名義変数です。

fit <- lm(data~age, data=data)
summary(fit)

Rで単回帰分析を実行するときのプログラムです。y＝data, x=ageです。ただしここではageが名義変数ですので解釈には注意が必要です。

> summary(fit)

Call:
lm(formula = data ~ age, data = data)

Residuals:
    Min      1Q  Median      3Q     Max 
-177.90  -85.25   -1.50   47.58  197.00 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1092.00      31.17  35.037  < 2e-16 ***
age70-75       83.90      44.08   1.903   0.0677 .  
age75-80      234.00      44.08   5.309 1.33e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 98.56 on 27 degrees of freedom
Multiple R-squared:  0.5173,    Adjusted R-squared:  0.4816 
F-statistic: 14.47 on 2 and 27 DF,  p-value: 5.365e-05

この結果から以下のことが分かります
age65-70の平均=1092
age70-75の平均=1092+83.9=1175.9
age75-80の平均=1092+234=1326

また一番下の行が分散分析の結果です。F検定のｐ値が<0.05なので３群のどこかに有意差があることが分かります。

分散分析

回帰分析の結果をanova関数に渡すことで分散分析表が出力されます（自由度、F値、p値は同じです）

anova(fit)

> anova(fit)
Analysis of Variance Table

Response: data
          Df Sum Sq Mean Sq F value    Pr(>F)    
age        2 281084  140542  14.468 5.365e-05 ***
Residuals 27 262275    9714                      

分散分析表

F値は回帰分析の結果と同じです。群間に有意な差があることが分かりました。一元配置分散分析における説明変数のカテゴリに基づいたグループ分けは、回帰分析におけるダミー変数による分析と本質的に同じ処理を行っており、同じデータ構造と同じ平方和の分割を用いているため、F値が同値になります。