比率の差の検定
ここでは、僕が考えた例題「リハビリの頻度に関する患者満足度調査」について考えます。全て架空の例題です。
例題 近年、医療の質を評価する指標として患者満足度調査を取り入れる病院が増加している。今回、リハビリの頻度に関する患者満足度調査を実施した結果を下記に示す。 A病院は平均週4回実施：満足116名、不満76名 B病院は平均週5回実施：満足244名、不満44名 満足と回答した患者の割合はA病院よりB病院が多いことを証明してください（有意水準2.5%） 帰無仮説: A病院の割合 ＝ B病院の割合 対立仮説: A病院の割合 < B病院の割合 注1) 患者属性、疾患、リハの種類などの要因は除外して考えます 注2) 数値は「改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎」より引用
このような例題を考える場合は、すぐにRで分割表を作成しましょう
mat <- matrix(c(116, 244, 76, 44), 2, 2)#2行,2列に並べる
rownames(mat) <- c("週4回", "週5回")
colnames(mat) <- c("満足", "不満")
mat
集計も追加します
addmargins(mat)
週4回で満足している割合：\(\frac{116}{192}\)
週5回で満足している割合：\(\frac{244}{288}\)
差の検定の前に独立性の検定をやってみましょう
chisq.test(mat)
p値は小さく、週５回の方が満足割合が多いようです
母比率の差の検定
Rを使用して検定します
prop.test(mat, correct = FALSE)
prop1=週4回で満足している割合
prop2=週4回で満足している割合
週５回の方が有意に多いことが分かりました
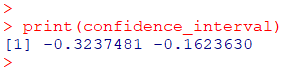
prop1-prop2の95％信頼区間は、-0.3237481 ～ -0.1623630となりました
検定の結果だけでよい人はここまでで結構です
正規分布を利用した検定
両グループの母集団から得られた確率変数\(X1, X2\)が二項分布に従う場合
\(X1 \sim B(n1, \pi1)\), \(X2 \sim B(n2, \pi2)\)
\(n_1, n_2\)が大きい場合、標本比率は正規分布に従う（大数の法則）
\(\hat{\pi}1-\hat{\pi}2 \sim N(\pi1-\pi2, \frac{\pi1(1-\pi1)}{n1}+\frac{\pi2(1-\pi2)}{n2})\)
zが標準正規分布に従うことを利用して検定を行う
\(\displaystyle z=\frac{(\hat{\pi}1-\hat{\pi}2)-(\pi1-\pi2)}{\sqrt{\frac{\hat{\pi}1(1-\hat{\pi}1)}{n1}+\frac{\hat{\pi}2(1-\hat{\pi}2)}{n2}}}\)
したがって、2つのサンプルの比率 \(\frac{116}{192}, \frac{244}{288}\) の母比率差も正規分布となります
\(\hat{\pi}_1-\hat{\pi}_2 \sim N(\pi_1-\pi_2,\frac{\pi_1(1-\pi_1)}{n_1}-\frac{\pi_2(1-\pi_2)}{n_2})\)
以下の統計量Zが正規分布(平均0、分散1の標準正規分布)に従うことを利用します
\(\displaystyle z=\frac{(\hat{\pi}_1-\hat{\pi}_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}}}\)
確率変数の分散の加法性 XとYが独立である場合 V(X ± Y)=V(X) + V(Y)
帰無仮説は \(\pi_1=\pi_2\) なので \(\pi_1-\pi_2=0\) の場合のｚ値を求めす
A1 = 116 #週4回満足
A2 = 76 #週4回不満
n1 <- A1 + A2 #週4回のn
B1 = 244 #週5回満足
B2 = 44 #週5回不満
n2 <- B1 + B2 #週5回のn
pi1 <- A1 / n1
pi2 <- B1 / n2
(z <- (pi2-pi1) / sqrt((pi1*(1-pi1)/n1) + (pi2*(1-pi2)/n2))) #Z値
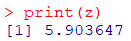
Z値 = 5.9 > 1.96 となるため帰無仮説は棄却されます（結論はｶｲ二乗検定と同じですね）
curve(dnorm(x), type="l", ylim=c(0, 0.5), xlim=c(-4, 4))
x <- qnorm(0.025, lower.tail=F) #これがZ値です
x1 <- seq(x, 5, length=100)
y <- dnorm(x1)
polygon(c(x1, rev(x1)), c(rep(0, length(x1)), rev(y)), col="pink")
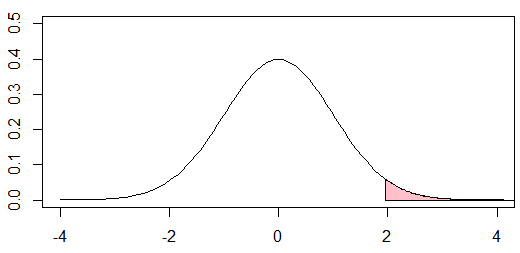
1.96はｐ＝0.025(ピンク色の部分)のときのＺ値（x軸）です
95％信頼区間の求め方
正規分布を利用して信頼区間を算出します
\(\displaystyle z=\frac{(\hat{\pi}_1-\hat{\pi}_2)-(\pi_1-\pi_2)}{\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}}}\)
\(\displaystyle \pi_1-\pi_2=(\hat{\pi}_1-\hat{\pi}_2)\pm{z}(\sqrt{\frac{\hat{\pi}_1(1-\hat{\pi}_1)}{n_1}+\frac{\hat{\pi}_2(1-\hat{\pi}_2)}{n_2}})\)
z = qnorm(0.025)
((116/192)-(244/288)) +
c(1, -1)*z*
sqrt((116/192)*(1-116/192)/192+(244/288)*(1-244/288)/288)
参考文献
コメント