
問題
袋Aに白玉2個、黒玉1個あります。袋Bは空です。 袋Aから一つ取り出して、袋Bに移します。 その後、袋Aの1個と袋Bの1個を入れ替えます。 さらに、袋Aの1個と袋Bの1個を入れ替えます。 袋Bに黒玉が残る確率を求めよ。
状態遷移図から求めます
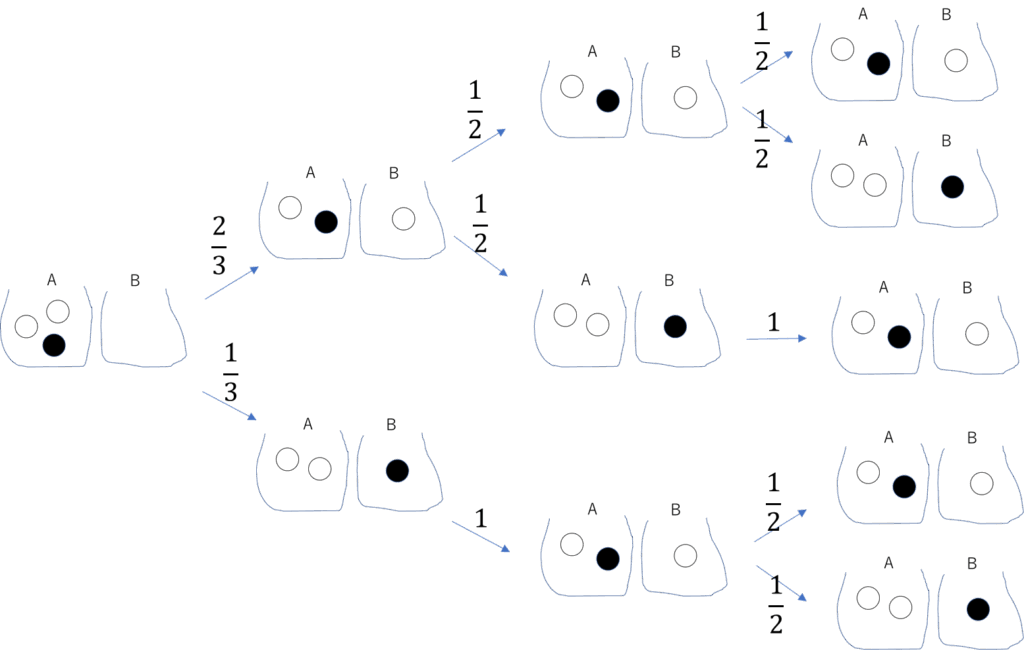
$\dfrac{2}{3}✕\dfrac{1}{2}✕\dfrac{1}{2}+\dfrac{1}{3}✕1✕\dfrac{1}{2}=\dfrac{1}{3}$
Rを使ったら、以下のようになります
R
# 玉の状態を記号で表す関数
format_state <- function(A, B) {
paste0("A:", paste(A, collapse=""), " B:", paste(B, collapse=""))
}
# 初期状態
initial_A <- c("W", "W", "B")
initial_B <- character(0)
# ステップ1:袋Aから1個を袋Bに移動(3通り)
step1_states <- list()
for (i in seq_along(initial_A)) {
new_A <- initial_A[-i]
new_B <- c(initial_B, initial_A[i])
step1_states[[length(step1_states)+1]] <- list(A=new_A, B=new_B)
}
# ステップ2:袋Aと袋Bの玉を1個ずつ入れ替え(全組合せ)
step2_states <- list()
for (s1 in step1_states) {
for (i in seq_along(s1$A)) {
for (j in seq_along(s1$B)) {
new_A <- s1$A
new_B <- s1$B
temp <- new_A[i]
new_A[i] <- new_B[j]
new_B[j] <- temp
step2_states[[length(step2_states)+1]] <- list(A=new_A, B=new_B)
}
}
}
# ステップ3:再度入れ替え(全組合せ)
final_states <- list()
for (s2 in step2_states) {
for (i in seq_along(s2$A)) {
for (j in seq_along(s2$B)) {
new_A <- s2$A
new_B <- s2$B
temp <- new_A[i]
new_A[i] <- new_B[j]
new_B[j] <- temp
final_states[[length(final_states)+1]] <- list(A=new_A, B=new_B)
}
}
}
# 袋Bに黒玉が残っている状態をカウント
black_in_B <- sum(sapply(final_states, function(s) "B" %in% s$B))
total <- length(final_states)
prob <- black_in_B / total
# 結果表示
cat("袋Bに黒玉が残る確率は", prob, "(", black_in_B, "/", total, ")です。\n")袋Bに黒玉が残る確率は 0.3333333 ( 1 / 3 )