このサイトでは離散型の関数を確率関数、連続型の関数を確率密度関数と使い分けています
ベルヌーイ試行
2種類の結果を生じる実験(例:成功 or 失敗)あるいは観察(例:陽性 or 陰性)を行った場合、一定の確率で2種類のどちらかが結果となります
このように2種類のどちらかが結果となる確率が一定で、同じ条件かつ独立に行う試行のことをベルヌーイ試行と言います
確率関数
結果が1となる確率 \(π\) のベルヌーイ試行を \(n\) 回実施して、結果が1となる回数を \(k\) とします
結果=1の回数が \(k\) 回となる確率を以下の関数で求めることができます
確率関数 \(P(X=k)={}_n C_kπ^k(1-π)^{n-k}\)
期待値 \(nπ\)
分散 \(nπ(1-π)\)
この確率の分布を二項分布、また確率変数\(X\)は二項分布に従うと言います

リハビリテーションでコインの表ウラは考えにくいので、以下のよなような例で説明します(僕が考えた架空のものですので、運動の定義などはカットしてます)
例題
地域Aの「週に1回以上の頻度で運動する人の割合」を50%とします. この地域からお互いに全く関係のない3名(Aさん、Bさん、Cさん)をランダムに選んで、「週に1回以上簡単な運動をしていますか?」というアンケートの結果を実施したとしましょう. 答えはもちろんYes=1、No=0のどちらかになります. 結果から確率を求めてみましょう・・・?
- Yesと答える確率は\(π=\frac{1}{2}\)
- 3名中Yesと答える人数 \(k\) のパターンは、0人、1人、2人、3人の4通りになります
- 考えられるパターンは以下の8通りになります
| X=k | Aさん | Bさん | Cさん | 確率 |
|---|---|---|---|---|
| 0 | No | No | No | 1/8 |
| 1 | Yes No No | No Yes No | No No Yes | 3/8 |
| 2 | Yes No Yes | Yes Yes No | No Yes Yes | 3/8 |
| 3 | Yes | Yes | Yes | 1/8 |
Yesの人数を確率変数\(X\)、試行回数3回、Yesとなる確率\(π=\frac{1}{2}\)とした場合、「\(X\)の確率は2項分布\(B(3 , 0.5)\)に従う」と表現します
これをグラフにすると以下のようになります
t <- 0:3
p <- dbinom(x = t, size = 3, prob = 0.5) #それぞれの確率を算出
barplot(p ~ t, pch = 16, xlab = "", ylab = "")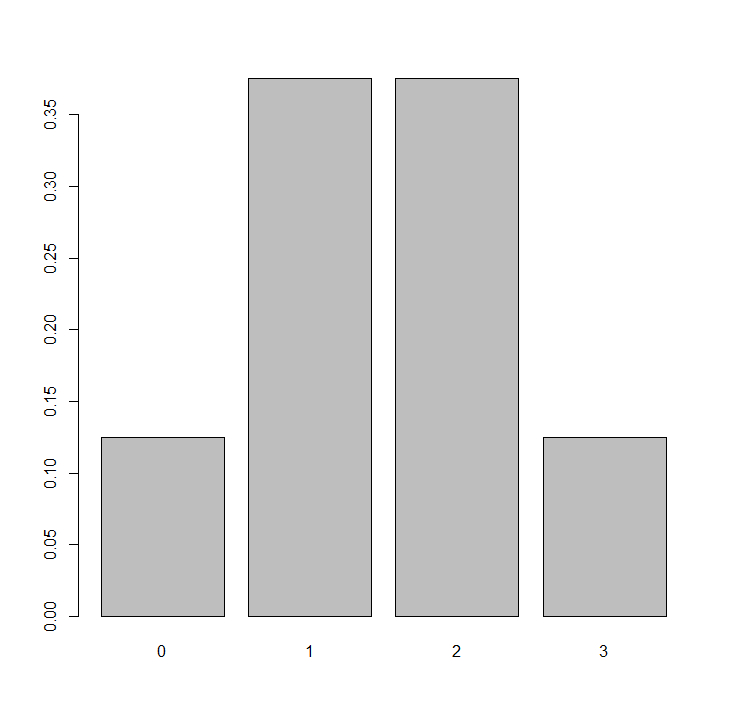
それぞれの確率はpの中に入っています

表に示した確率と同じ値になります
Rで確率を求めるときは以下のように書きます
- P(X≧1)=0.375+0.375+0.125=0.875を求めたい場合(q = 0に注意)
pbinom(q = 0, size = 3, prob = 0.5, lower.tail = FALSE) 
lower.tail = FALSE はX≦0を含めないという意味になり、\(P(X≧1)\) を求めることとなります
- P(X≦1)=0.5を求めたい場合
pbinom(q = 1, size = 3, prob = 0.5, lower.tail = TRUE)lower.tail = TRUE はTRUEなのでX≦1を含めるという意味になり、\(P(X≦1)\) を求めることになります

地域の確率が30%で、50人に調査した場合は、・・・手計算でやるのは大変なのでRで算出してみましょう
t <- 0:50
p <- dbinom(x = t, size = 50, prob = 0.3) #それぞれの確率を算出
barplot(p ~ t, pch = 16, xlab = "", ylab = "")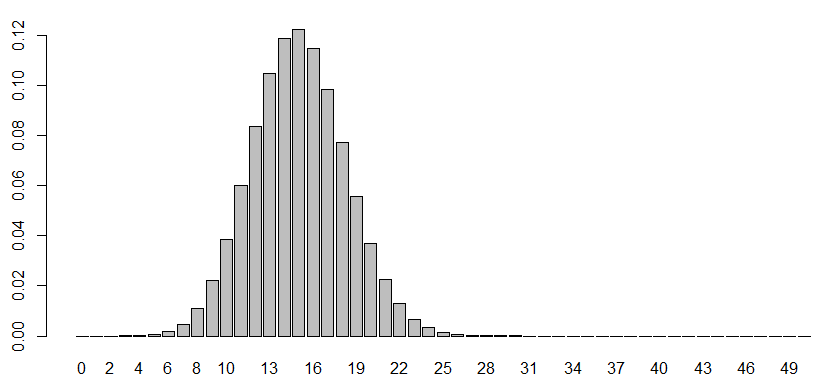
確率はいかのようになります
確率変数15のときの確率が最も高い確率を示しています
また、ほとんど正規分布になることも理解できます
このことは二項分布の期待値が \(nπ\) なので、中心極限定理より説明できます
母集団の分布がどのような分布であっても、無作為抽出した標本における標本平均の分布は、標本の大きさnが大きいときに正規分布に収束する
確率0.3, k=2, 3, 5, 10, 50, 100の二項分布
つまり\(B(2, 0.3)\), \(B(3, 0.3)\), \(B(5, 0.3)\), \(B(10, 0.3)\), \(B(50, 0.3)\), \(B(100, 0.3)\)
fun <- function(k){
t <- 0:k
p <- dbinom(x = t, size = k, prob = 0.3) #それぞれの確率を算出
barplot(p ~ t, pch = 16, xlab = "", ylab = "")
}
par(mfrow = c(2,3))
for(k in c(2,3,5,10,50,100)){fun(k)}
par(mfrow = c(1,1))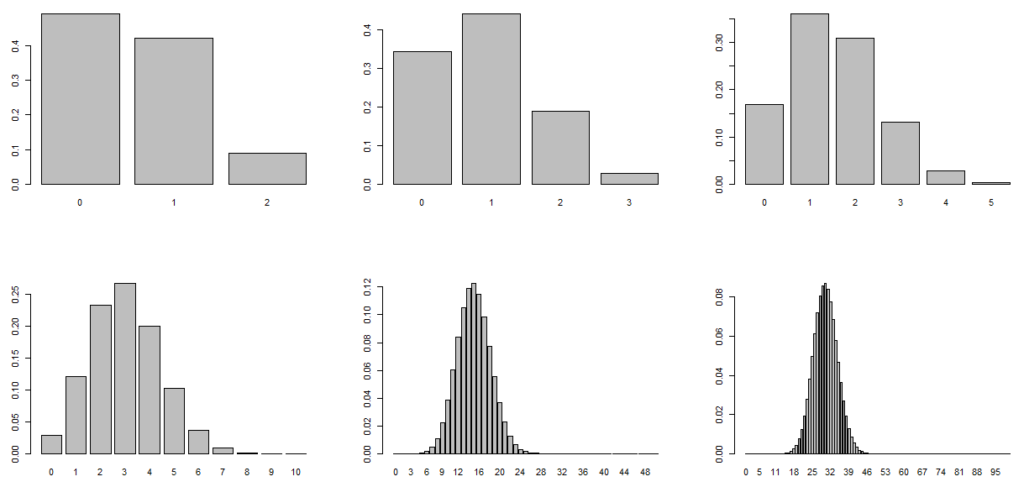
ベルヌーイ分布
確率\(π\)で2種類の結果(0または1)の値をとる独立した\(1\)回の試行で得られる結果の分布をベルヌーイ分布という
期待値 \(π\)
分散 \(π(1-π)\)
もちろん二項分布の\(n=1\)と同じ結果なので、\(B(1,π)\)と表される場合もあります