ロジスティック回帰(2) - 統計学備忘録

ロジスティック回帰 (1)の続きです。例題はロジスティック回帰 (1)と同じですが、データセットの構造が異なります。例題の内容や結果については色々とご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。

例題
リハビリを受けている入院中の患者に対してリハビリに関する満足度調査を実施した。1週間に割り当てられた単位数をもとにランダムにインタビューした。「満足」と回答する割合と1週間のリハビリ単位数には関係があるのでしょうか？

データの準備と要約
ロジスティック回帰
- fit1: dat1 を使用したロジスティック回帰
- fit2: dat2 を使用したロジスティック回帰
deviance
- fit1のdeviance
- fit2のdeviance
AIC（赤池情報量規準: Akaike’s Information Criterion）

データの準備と要約

データセット log01 と log02 をダウンロードします（ファイルの読み込み方）

log01 ダウンロード

dat1 <- read.csv("log01.csv", header=T, fileEncoding = "UTF-8")

log02 ダウンロード

dat2 <- read.csv("log02.csv", header=T, fileEncoding = "UTF-8")

dat1の確認

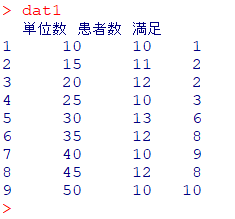
dat1

単位数＝1週間のリハ単位数
患者数＝各単位数に該当する患者数
満足＝「満足」と回答した患者数

dat2の確認

dim(dat2)

100行あるので20行のみを表示してみます

#20行のみ表示
dat2[0:20,]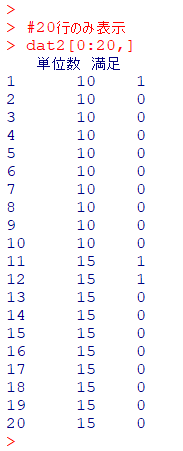

ロジスティック回帰

それぞれのセットでロジスティック回帰を実行してみます

目的変数の設定が異なるので注意してください

fit1: dat1 を使用したロジスティック回帰

fit1 <- glm(
    cbind(満足, 患者数-満足) ~ 単位数, 
    family=binomial, 
    data=dat1
)
summary(fit1)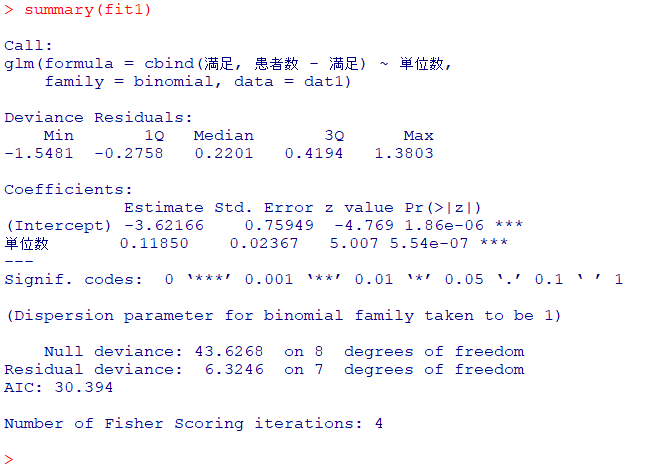

fit2: dat2 を使用したロジスティック回帰

fit2 <- glm(
    cbind(満足, 1-満足) ~ 単位数, 
    family=binomial, 
    data=dat2
)
summary(fit2)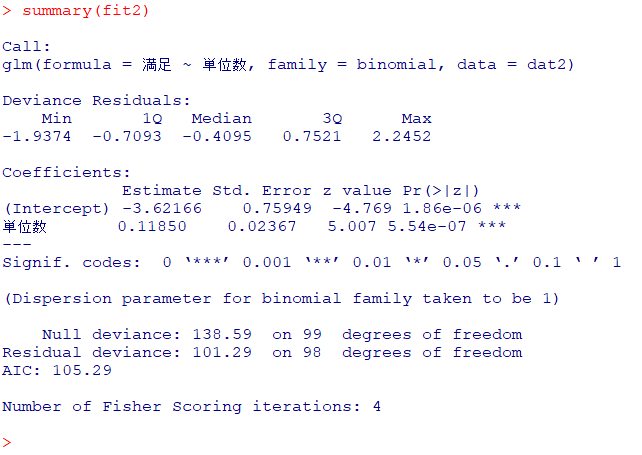

fit1とfit2で異なる部分はdevianeceの部分です

逸脱度(deviance) = -2 × 対数尤度

以下はRの出力のまとめです（Rは尤度比検定に必要なNull deviance、Residual devianceを出力します）

Null deviance：切片モデルのdevianceから尤も当てはまりのよいモデル（Full model）のdevianceを引いた値

Residual deviance：回帰モデルのdevianceから尤も当てはまりのよいモデル（Full model）のdevianceを引いた値

	fit1	fit2
Null deviance	43.6268	138.59
Null devianceの自由度	8	99
Residual deviance	6.3246	101.29
Residual devianceの自由度	7	98
AIC	30.394	105.29

この違いから、fit1とfit2では対数尤度が異なることが理解できます

deviance

fit1のdeviance

$y_i=$満足の数$、n_i=$患者数$、i=1,2,3, \dotsm ,9$ （ロジスティック回帰 (1)より）

対数尤度

$=L_{\theta1}=log(\prod_{i=1}^{n} (P_i^{y_i}(1-P_i)^{n_i-y_i}))$

$\quad=log(\prod_{i=1}^{9} (P_i^{y_i}(1-P_i)^{n_i-y_i}))$

$\quad=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))+Const.$

fit1の最大逸脱度

fit1_null <- glm(
    cbind(満足, 患者数-満足) ~ 1, 
    family=binomial, 
    data=dat1
)

Dmax1 <- -2*logLik(fit1_null)
print(Dmax1)

fit1モデルの逸脱度

Dreg1 <- -2*logLik(fit1)
print(Dreg1)

fit1の最小逸脱度

二項分布より全ての確率から尤度を算出して対数尤度を求めます

Dmin1 <- -2*sum(log(dbinom(dat1$満足, dat1$患者数, dat1$満足/dat1$患者数)))
print(Dmin1)

最大逸脱度と最小逸脱度との差がNull devianceになります

Rでは Null deviance と Residual deviance が算出されます

Null deviance（最大逸脱度$-$最小逸脱度）

Dmax1 - Dmin1

Residual deviance（回帰分析モデルの逸脱度$-$最小逸脱度）

Dreg1 - Dmin1

fit2のdeviance

$y_i=$満足の数$(0, 1)、n_i=1、i=1,2,3, \dotsm ,100$

fit2_null <- glm(
    cbind(満足, 1-満足) ~ 1, 
    family=binomial, 
    data=dat2
)
summary(fit2_null)

fit2の最大逸脱度

Dmax2 <- -2*logLik(fit2_null)
print(Dmax2)

fit2モデルの逸脱度

Dreg2 <- -2*logLik(fit2)
print(Dreg2)

fit2の最小逸脱度

dat2の場合はグループデータではなく全てのデータが対象となっており対数尤度＝0となります

したがって最小逸脱度＝0

#回帰分析モデルの逸脱度
-2*logLik(fit2)

#-2*対数尤度からも同じ答えが算出されます
b0 <- summary(fit2)$coef[1, 1] 
b1 <- summary(fit2)$coef[2, 1]
print(c(b0, b1))
-2*sum(dat2$満足*(b0+b1*dat2$単位数) - log(1 + exp(b0+b1*dat2$単位数)))