データの準備と要約

これは僕が作った架空の例題です。結果についてはご意見があると思いますが、ANCOVAの理解のための例題になっておりますのでご了承ください。
例題) 歩行可能な脳卒中患者を対象にした後ろ向き観察研究です。歩行練習A(10名)と歩行練習B(10名)を受けた20名の10m歩行時間の短縮時間を調べました。
データセットancovaをdatに格納します(ファイルの読み込み)
data <- read.csv("ancova.csv", header=T, fileEncoding = "UTF-8")
head(data)> head(data)
ID gait pre short
1 1 B 22.5 5.6
2 2 A 25.5 7.8
3 3 B 19.3 3.3
4 4 A 25.6 9.6
5 5 A 31.2 10.8
6 6 B 16.5 4.0gait: 歩行練習の種別
pre: 練習実施前の10m歩行時間
short: 歩行練習実施による10m歩行の短縮時間
歩行練習はfactor型に置換しておきましょう
data$gait <- as.factor(data$gait)
levels(data$gait)> levels(data$gait)
[1] "A" "B"factor() 関数は名義変数をカテゴリカル変数(因子型変数)に変換し、データのカテゴリーは「水準」として定義されます。levels() 関数で表示されるカテゴリカル変数の水準のうち、最初に表示されるカテゴリーがデフォルトで基準カテゴリー(参照カテゴリー)となり、統計モデルでの比較の基点として機能します。relevel() 関数や factor() 関数の levels 引数を使用することで、レベルの順序を指定し、基準カテゴリーを変更することが可能です。
要約
summary(data)> summary(data)
ID gait pre short
Min. : 1.00 A:10 Min. :16.50 Min. : 3.300
1st Qu.: 5.75 B:10 1st Qu.:22.10 1st Qu.: 4.075
Median :10.50 Median :24.00 Median : 5.550
Mean :10.50 Mean :24.95 Mean : 6.430
3rd Qu.:15.25 3rd Qu.:28.52 3rd Qu.: 8.600
Max. :20.00 Max. :35.00 Max. :12.200 歩行練習の各群の要約
色々な方法があると思いますが、ここではパッケージを使用しない方法で
summary(data[data$gait == "A", 2:4])
summary(data[data$gait == "B", 2:4])> summary(data[data$gait == "A", 2:4])
gait pre short
A:10 Min. :22.20 Min. : 5.500
B: 0 1st Qu.:25.52 1st Qu.: 6.675
Median :27.45 Median : 8.600
Mean :28.20 Mean : 8.660
3rd Qu.:30.80 3rd Qu.:10.500
Max. :35.00 Max. :12.200
> summary(data[data$gait == "B", 2:4])
gait pre short
A: 0 Min. :16.50 Min. :3.30
B:10 1st Qu.:19.93 1st Qu.:3.30
Median :22.05 Median :4.05
Mean :21.71 Mean :4.20
3rd Qu.:22.48 3rd Qu.:4.95
Max. :28.50 Max. :5.60 2群の差の検定
箱ひげ図
boxplot(short ~ gait, data=data)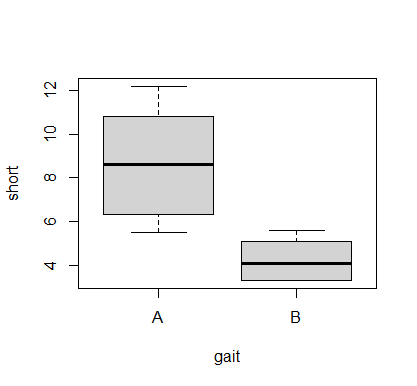
歩行練習Aと歩行練習Bでは随分差があるようです(歩行練習A>歩行練習B)
t検定
2群の差の平均値を比較検定してみます
t.test(short ~ gait, data=data)> t.test(short ~ gait, data=data)
Welch Two Sample t-test
data: short by gait
t = 5.7238, df = 11.933, p-value = 9.757e-05
alternative hypothesis: true difference in means between group A and group B is not equal to 0
95 percent confidence interval:
2.761205 6.158795
sample estimates:
mean in group A mean in group B
8.66 4.20 歩行練習の違いにより歩行時間短縮が有意に異なることが分かりました。練習Aの方が10m歩行時間短縮には有効である(95%信頼区間は2.76~6.16)・・・と単純に結果を出してもよいでしょうか?。練習前の10m歩行時間が影響しており、もともと時間がかかる人は短縮時間も長くなるのでは・・・?。その疑問に答えるために共分散分析を行います。
Rで共分散分析を実行
歩行練習AとBをグラフで確認
fig1 <- function() {
pchAB <- ifelse(data$gait == "A", 19, 21)
plot(data$pre, data$short,
pch=pchAB, cex=1.5,
xlab="練習前の10m歩行時間", ylab="短縮時間",
col = ifelse(data$gait == "A", "blue", "red"))
modelA <- lm(short ~ pre, data=data, subset=gait=="A")
a_xmin <- min(data$pre[data$gait == "A"])
a_xmax <- max(data$pre[data$gait == "A"])
a_coef <- coef(modelA)
segments(a_xmin, a_coef[1] + a_coef[2] * a_xmin,
a_xmax, a_coef[1] + a_coef[2] * a_xmax, col="blue")
modelB <- lm(short ~ pre, data=data, subset=gait=="B")
b_xmin <- min(data$pre[data$gait == "B"])
b_xmax <- max(data$pre[data$gait == "B"])
b_coef <- coef(modelB)
segments(b_xmin, b_coef[1] + b_coef[2] * b_xmin,
b_xmax, b_coef[1] + b_coef[2] * b_xmax, col="red")
legend("topleft",
legend = c("練習A", "練習B"),
pch = c(19, 21),
col = c("blue", "red"))
}
fig1()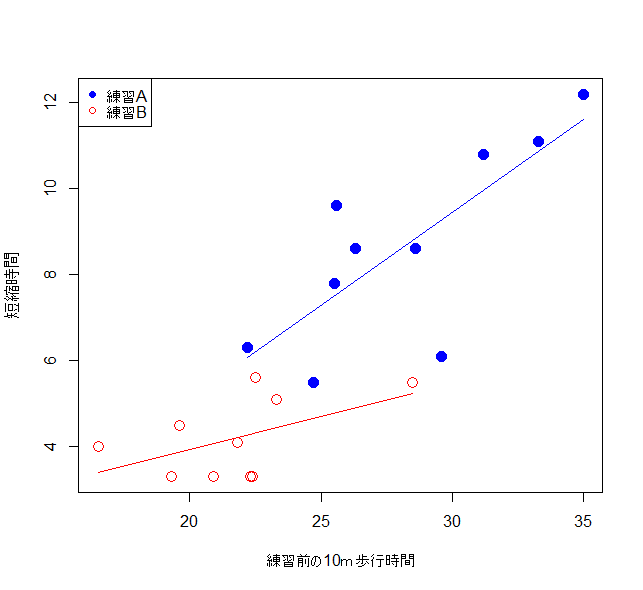
練習Aは歩行速度が遅い患者に適応されていたようです。このような場合には、歩行練習前の10m歩行時間を考慮した解析が必要になります(これが共分散分析になります)。歩行練習前の10m歩行時間を共変量として(歩行時間を考慮して)回帰分析を実施します。
Rで実施する場合は、重回帰分析と同じ方法です
fit <- lm(short ~ gait + pre, data=data)
summary(fit)
confint(fit)> summary(fit)
Call:
lm(formula = short ~ gait + pre, data = data)
Residuals:
Min 1Q Median 3Q Max
-3.0202 -0.7083 -0.0401 1.0303 1.7947
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.61018 2.42519 -0.252 0.80436
gaitB -2.32654 0.80219 -2.900 0.00996 **
pre 0.32873 0.08474 3.879 0.00121 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.306 on 17 degrees of freedom
Multiple R-squared: 0.8119, Adjusted R-squared: 0.7898
F-statistic: 36.69 on 2 and 17 DF, p-value: 6.797e-07
> confint(fit)
2.5 % 97.5 %
(Intercept) -5.7268761 4.5065125
gaitB -4.0190108 -0.6340757
pre 0.1499362 0.5075235歩行練習Bの推定値が-2.32654となっています。これは歩行練習B群に比べて、歩行練習S群の短縮時間が平均2.32秒長いという結果になります。
結果の解釈
fig1 <- function() {
pchAB <- ifelse(data$gait == "A", 19, 21)
plot(data$pre, data$short,
pch = pchAB, cex = 1.5,
xlab = "練習前の10m歩行時間", ylab = "短縮時間",
col = ifelse(data$gait == "A", "blue", "red"))
modelANCOVA <- lm(short ~ pre + gait, data = data)
ancova_coef <- coef(modelANCOVA)
a_xmin <- min(data$pre[data$gait == "A"])
a_xmax <- max(data$pre[data$gait == "A"])
a_ymin <- ancova_coef[1] + ancova_coef[2] * a_xmin
a_ymax <- ancova_coef[1] + ancova_coef[2] * a_xmax
segments(a_xmin, a_ymin, a_xmax, a_ymax, col = "blue", lwd = 2, lty = 2)
b_xmin <- min(data$pre[data$gait == "B"])
b_xmax <- max(data$pre[data$gait == "B"])
b_ymin <- (ancova_coef[1] + ancova_coef[3]) + ancova_coef[2] * b_xmin
b_ymax <- (ancova_coef[1] + ancova_coef[3]) + ancova_coef[2] * b_xmax
segments(b_xmin, b_ymin, b_xmax, b_ymax, col = "red", lwd = 2, lty = 2)
modelA <- lm(short ~ pre, data=data, subset=gait=="A")
a_coef <- coef(modelA)
segments(a_xmin, a_coef[1] + a_coef[2] * a_xmin,
a_xmax, a_coef[1] + a_coef[2] * a_xmax, col="blue")
modelB <- lm(short ~ pre, data=data, subset=gait=="B")
b_coef <- coef(modelB)
segments(b_xmin, b_coef[1] + b_coef[2] * b_xmin,
b_xmax, b_coef[1] + b_coef[2] * b_xmax, col="red")
legend("topleft",
legend = c("歩行練習A", "歩行練習B", "ANCOVA_A", "ANCOVA_B"),
pch = c(19, 21, NA, NA),
col = c("blue", "red", "blue", "red"),
lty = c(NA, NA, 2, 2),
lwd = c(NA, NA, 2, 2))
}
fig1()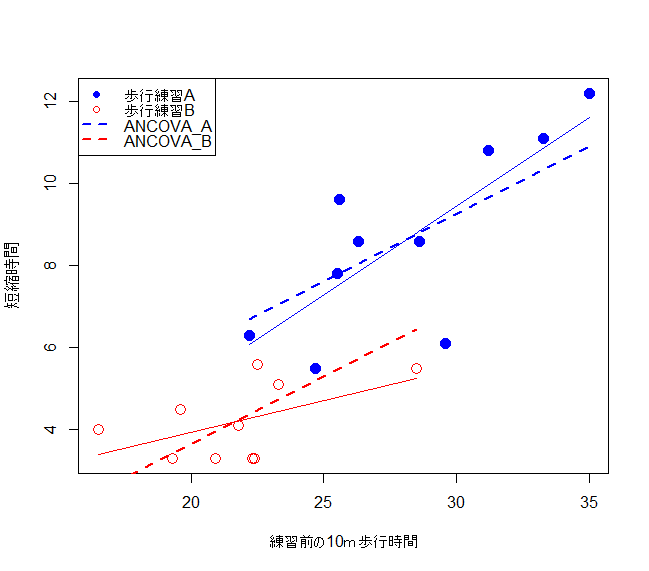
上図の青の点線と赤の点線は、歩行練習A群と歩行練習B群に共通する傾き(0.33)を持っています。青の線の切片は、-0.61です。赤の線の切片は、-0.61018-2.32654=-2.93672となります。両群の「切片」の差は、練習前の時間を共変量に入れた歩行練習AとBの差2.32(95%信頼区間:0.63~4.02)になります。練習前の時間を考慮することで、さきほどのt検定の結果(95%信頼区間:2.76~6.16)よりも差が小さいことが理解できます。

2群の差の検定だけでは読み取れなかった違いを吟味することができました。結果だけでよければここまでです。次からはもう少し詳しく勉強してみます。

