僕が作った架空のデータで練習しましょう。結果についてはご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。
例題）回復期病棟に入院した脳卒中患者を対象としました。FIM利得（退棟時 FIM－入棟時 FIM）を入棟時のFIM、入院期間の理学療法の時間、入棟時のBMIで予測します
データの準備と要約
データセット jukaiki をdatに格納します（ファイルの読み込み）
csvファイルを直接開くと文字化けしています。Rでファイルを読み込んで使用してください。
使用するパケージ
library(tidyverse)
library(BlandAltmanLeh)
head(dat)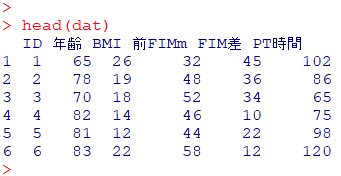
dim(dat)
n=50, 5変数からなるデータセット
FIM差：退棟時 FIM－入棟時 FIM
BMI：入棟時のBMI
前FIMm：入棟時のFIM運動項目得点
PT時間：入院期間に理学療法を実施した時間
n=49
目的変数をFIM差として、説明変数を前FIMm、PT時間、BMIとした重回帰分析をRで実行してみましょう（関数lmは単回帰と同じです）
目的変数の分布を確認してみましょう
hist(dat$FIM差)
もし残差に偏りがあるのであれば再考しなければなりません
重回帰分析
fit <- lm(
FIM差 ~ BMI + 前FIMm + PT時間 ,
data=dat
)
summary(fit)
前FIMmとPT時間のｐ値は＜0.05ですので、この2つの変数でＦＩＭ差を予測する予測式が成立します
p>0.05になったBMIについては吟味しなければなりません
予測式を分かり易く書くと以下のようになります
FIM差 = 31.48 – 0.51*前FIMm + 0.15*PT時間
僕が作ったデータを使っているので実際にはあり得ませんが、上記の予測式を解釈すると・・・「入棟時のFIM運動項目が1点上がるとFIM利得は0.51低くなる・・・これは天井効果も考えられると思いますが、入棟時の得点が低いと伸びしろが大きいと考えられます。また入棟時の運動機能を考慮した場合でも、PT時間が1時間増えるとFIM利得は0.15増加するようです。」というようなことが研究計画に応じて考察できます。（ややPTに肩入れしたデータになっていますね・・・すみません）
これでRを使用した重回帰分析が実行できるようになりました
結果のみでよければ、ここまでです
ここらかはもう少し詳しく学習してみましょう
統計モデル
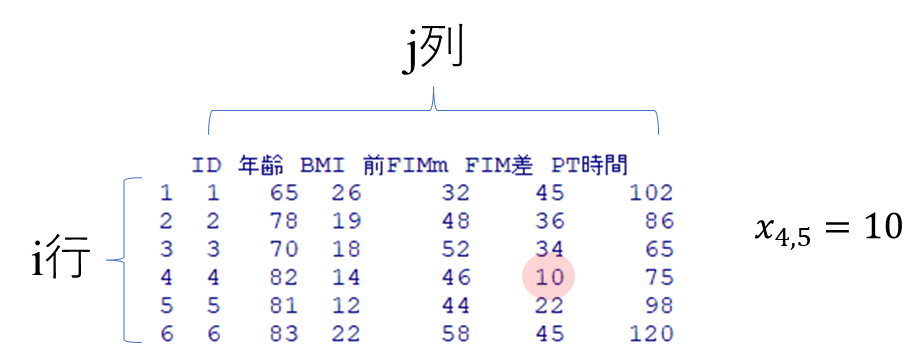
このサイトでは次のような標記に従います
$x_{i,j}$ の場合、$i$ はデータセットの行、$j$ はデータセットの列を示します
しかし統計モデルを書くときにはやや趣が異なりますのでご理解ください
今回の例では、重回帰分析によりFIM差を予測することが目的です
統計モデルは以下のようになります
$\hat{y_i}=\beta_0+\beta_1x_{i1}+ \dotsc +\beta_jx_{ij}+e_{i} \qquad e_{i} \sim N(0,\sigma^2)$
ここで重要なのは誤差が正規分布に従うことを仮定していることです
$e_{i} \sim N(0,~\sigma^2)$
つまり 残差=$y_i-\hat{y_i}$ は正規分布に従うことを仮定して分析が進んで行きます
回帰分析後の残差分析は重要ですね。残差分析はあとで説明します。
今回の例では
$\hat{y_i}=\beta_0+\beta_1x_{i1}+ \dotsc +\beta_jx_{ij}+e_{i} \quad ( i=0,1,\dotsc,50, \quad j=5 )$
$\hat{} \quad$はハットと読み、FIM差の予測値を表します
重回帰分析の結果、以下のような予測式が成立しました
$\hat{y_i}=\beta_0+\beta_1x_{i1}+\beta_2x_{i2}+\beta_3x_{i3}$
$y_i$：サンプルのFIM差（実際のデータ）
$\hat{y_i}$：回帰式から予測されるFIM差（予測値）
FIM差$=y_i$
前FIMm$=x_{i1}$
PT時間$=x_{i2}$
BMI$=x_{i3}$
この書き方が苦手、よく理解できない・・・という人も多いかと思いますが、徐々に慣れてくると思います。
回帰係数の推定
単回帰分析や重回帰分析の係数の求め方のページにも記載しております
単回帰分析と同様に誤差二乗の総和が最小になるパラメタを推定します（最小二乗法）
誤差二乗和=$\sum(y_i-(\beta_0+\beta_1x_{i1}+ \dotsc +\beta_jx_{ij}))^2$
これで $\beta_0 \sim \beta_j$ で偏微分して求めるのですが、線形代数で解いた方が簡単です
表記の定義：$x_{ij}$の場合、$i$はデータセットの行、$j$はデータセットの列を示す
$y_{i}=b_0+b_1x_{ij}+\dotsc+b_jx_{ij}+\varepsilon_{i} \quad i={1,2,\dotsc,n} \quad j={1,2,\dotsc,k}$
\(
\mathbf{X}=
\left(\begin{array}{ccc}
1 & x_{11} & \dotsc & x_{1k} \\
1 & x_{21} & \dotsc & x_{2k} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{n1} & \dotsc & x_{nk}
\end{array}\right)
\)
\(
\mathbf{y}=
\left(\begin{array}{cc}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{array}\right)
\quad\)\(
\mathbf{b}=
\left(\begin{array}{cc}
b_0 \\
b_1 \\
\vdots \\
b_k
\end{array}\right)
\quad\)
とした場合、パラメタ推定の公式は以下のようになります
$\mathbf{b}=(\mathbf{X^T}\mathbf{X})^{-1}\mathbf{X^T}\mathbf{y}$
実際にdatのデータを挿入して求めてみましょう（ここではパイプ演算子を使って記述してみます）
mat <- dat %>%
mutate(b = c(rep(1, dim(dat)[1]))) %>%
select(b, BMI, 前FIMm, PT時間,) %>%
as.matrix()
solve(
t(mat) %*% mat) %*%
t(mat) %*%
dat$FIM差
# %*% この記号は行列の掛け算です
lm関数で算出した係数と同じ値を求めることができました
残差分析
実測値 $y_i$ と回帰式から得られる値 $\hat{y_i}$ をプロットしてみましょう
#切片
b0 <- coef(fit)[1]
#BMI
b1 <- coef(fit)[2]
#前FIMmの係数
b2 <- coef(fit)[3]
#PT時間
b3 <- coef(fit)[4]
print(c(b0, b1, b2, b3))
FIM差の予測式から求めた予測値
yhat1 <- b0 + b1*dat$BMI + b2*dat$前FIMm + b3*dat$PT時間
Rのpredict関数を使えば予測値を簡単に求めることができます
yhat2 <- predict(fit)
# yhat1 = yhat2
FIM差をx軸、FIM差の推定値をy軸にして、誤差を確認します
plot(dat$FIM差, yhat1, xlim = c(0, 50), ylim = c(0, 50))
# Y=Xの直線
segments(
x0=0, y0=0,
x1=50, y1=50
)
#誤差の例
segments(
x0=dat$FIM差[3], y0=yhat1[3],
x1=dat$FIM差[3], y1=dat$FIM差[3],
col="red"
)
＊ yhat1 を yhat2 に変えても全く同じグラフになります
Y=Xの線上からのズレ（赤線）が誤差になります
Bland Altman Plotで確認してみます
ba <- BlandAltmanLeh::bland.altman.stats(
dat$FIM差, yhat1
)
#str(ba)で確認して必要な部分だけ抜き取ります
plot(
ba$means, ba$diffs,
xlab="FIM差とyhat1の平均値",
ylab="FIM差とyhat1との差"
)
abline(h=0, lty=2, col=2)
０を中心になんとなく正規分布しているようです
次に残差のヒストグラムを見てみます
hist(
dat$FIM差-yhat1,
main="残差",
xlab="", ylab=""
)
正規分布の形状のようです
QQプロット
qqnorm(dat$FIM差-yhat1)
qqline(dat$FIM差-yhat1)
正規分布していることが確認できました
回帰分析表と分散分析表
回帰分析表
#再掲
fit <- lm(
FIM差 ~ BMI + 前FIMm + PT時間 ,
data=dat
)
summary(fit)
今度は決定係数やF値が見えるところまでペーストしておきます
信頼区間と予測区間
導出は後日アップします！今回は方法のみ書いておきます。
#係数の信頼区間
confint ( fit , level = 0.95 )
#予測値の信頼区間
con <- predict(fit, newdata = dat, interval = 'confidence', level = 0.95)
head(con)
#予測値の予測区間
pre <- predict(fit, newdata = dat, interval = 'prediction', level = 0.95)
head(pre)
分散分析表
分散分析で詳細を説明しています
anova(fit)
２つの表がどのような関係になっているのか確認してみましょう
残差平方和（ここではSresとします）
回帰分析の結果から求めてみます
#回帰式から得た予測値と実際の値の差の二乗和
Sres <- sum((dat$FIM差 - yhat1)^2) %>%
print()
分散分析表（Residuals）と同じ値になります
anova(fit)$Sum[4]
回帰モデルの平方和（ここではSregとします）
#回帰分析より
#回帰式から得た予測値と実際の値の平均値との差の二乗和
Sreg <- sum((yhat2 - mean(dat$FIM差))^2) %>%
print()
#分散分析表も同じ値を求めることができます
#BMI, 前FIMm、PT時間のSum Sq（平方和）の総和
anova(fit)$Sum[1:3] %>%
sum()
Residual standard error (残差の標準誤差)
回帰分析と分散分析表から求めることができます
$残差の標準誤差＝\sqrt{\dfrac{残差平方和}{自由度}}$
#回帰分析表より
#残差平方和=Sres
#残差の自由度＝サンプルサイズ-変数の数-１
Sres_df <- dim(dat)[1]-3-1
#残差の標準誤差
sqrt(Sres/Sres_df)
#分散分析表より
sqrt(anova(fit)$Sum[4]/anova(fit)$Df[4])
Multiple R-squared (決定係数)
#回帰分析の結果より
#回帰式から得た平方和=Sreg
#残差平方和 =Sres
1 - Sres / (Sreg+Sres)
#分散分析表より
全平方和 <- sum(anova(fit)$Sum)
残差平方和 <- anova(fit)$Sum[4]
1 - (残差平方和 / 全平方和)
Adjusted R-squared (自由度調整済み決定係数)
平方和を自由度で調整した決定係数
残差の変動 = 残差平方和÷自由度（サンプルサイズー変数の数ー1）
全体の変動 = 全平方和÷自由度（サンプルサイズー1）
Adjusted R-squared = $1-\dfrac{残差の変動}{全体の変動}$
#回帰式からの平方和=Sreg
#残差平方和=Sres
#残差の自由度＝Sres_df
#全平方和
Sall <- Sres + Sreg
#全平方和の自由度
df <- dim(dat)[1]-1
#Adjusted R-squared
1 - (Sres / Sres_df)/(Sall/ df)
#分散分析表より
an <- anova(fit)
1-(an$Sum[4]/an$Df[4]) / (sum(an$Sum[1:4]/df))
F値
F分布を使用して回帰式全体の検定を行う
帰無仮説：$\beta_0=\beta_1= \dotsb = \beta_j=0$
つまり帰無仮説が棄却されなければ「この回帰式は全く意味がない」ということになります
$Fvalue = \dfrac{\dfrac{Sreg}{df}}{\dfrac{Sres}{Sres\_df}}$
同じF値を求めることができます
#回帰分析より
#残差平方和＝Sres
#回帰式からの平方和=Sreg
Fvalue1 <- (Sreg/3)/(Sres/(49-3-1))
print(Fvalue1)
#分散分析表より
S0 <- sum(anova(fit)$Sum)
S1 <- anova(fit)$Sum[4]
Fvalue2 <- ((S0 - S1)/3)/(S1/(49-3-1))
print(Fvalue2)
あとはF分布に従って検定します
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください