正規分布

通常はNormal distributionと呼ばれているのですが、この分布はC.F.ガウス(1777-1855)の誤差関数に由来することからGaussian distributionとも呼ばれています。正規と呼んだのはF.ゴルトンです（統計学入門, 東京大学出版より）。Wikipediaでは、「正規分布はアブラーム・ド・モアブルによって1733年に導入された」とも書かれています。

正規分布

平均 \(\mu\), 分散 \(\sigma^2\) に従う正規分布を \(N\sim(\mu, \, \sigma^2)\) と標記します

確率密度関数：\(f(x)=\dfrac{1}{\sqrt{2\pi\sigma^2}}exp(-\dfrac{(x-\mu)^2}{2\sigma^2}) \qquad (-\infty<x<\infty)\)

期待値：\(\mu\)

分散：\(\sigma^2\)

\(N\sim(5, \, 2^2)\)

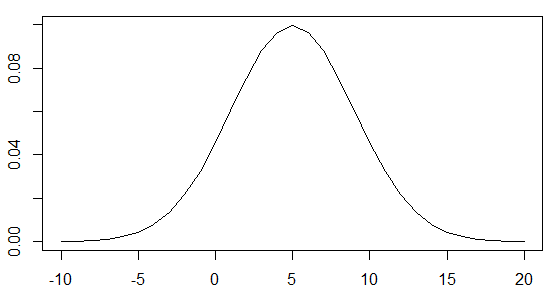
#グラフ
x <- seq(-10, 20, length(100))
plot(x, dnorm(x, 5, 4),type="l")

ただ描けばよいときは、こちらが簡単

正規分布の性質

#グラフ
curve(dnorm(x,5,4),-10,20)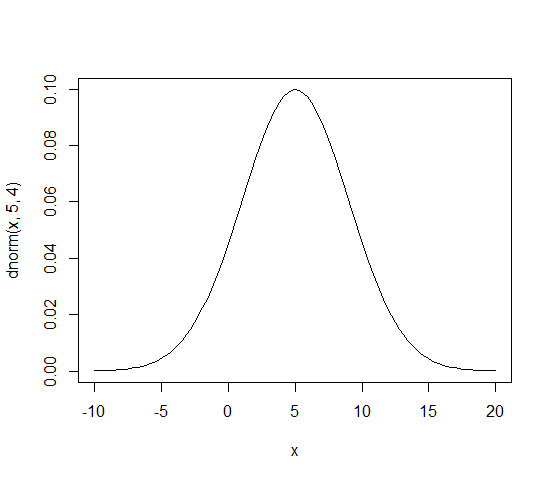

線形変換した場合

確立変数 \(X\) が \(N\sim(\mu, \, \sigma^2)\) に従うとき、\(aX+b\) も正規分布に従う

期待値：\(E(aX+b)=a\mu+b\)

分散：\(V(aX+b)=a^2\sigma^2\)

\(aX+b\) は \(N\sim(a\mu+b,\, a^2\sigma^2)\) に従う

標準正規分布

確立変数 \(X\) が \(N\sim(\mu, \, \sigma^2)\) に従うとき、

標準化変数 \(Z=\dfrac{X-\mu}{\sigma}\) は \(N \sim (0, \, 1)\) に従う

これを標準正規分布という　平均 \(0\), 分散 \(1\) に従う正規分布 \(N\sim(0, \, 1)\)

確率密度関数：\(f(Z)=\dfrac{1}{\sqrt{2\pi}}exp(-\dfrac{Z^2}{2})\)

• \(Z=\dfrac{X-\mu}{\sigma}\) を\(Z\)値、\(Z\)スコアといいます
• この値を使用した検定が\(Z\)検定です

正規分布の再生性

確立変数 \(X, \, Y\) がそれぞれ \(N \sim (\mu_1, \, \sigma_1^2), \, N \sim (\mu_2, \, \sigma_2^2)\) に従う場合

\(X+Y\)は \(N \sim (\mu_1+\mu_2, \, \sigma_1^2 + \sigma_2^2)\)に従う

P値

標準正規分布における上側P値＝0.025の例

上側ｐ値が0.025のときの確立変数 \(Z\) の求め方は（\(Z\) 値）

#統計量
qnorm(0.025, lower.tail=F)

有意水準5％による \(Z\) 検定の例

データの誤差平均が標準正規分布に従うと仮定して、平均値が約1.96より大きくなった場合に有意である（平均が０ではない）と判断します

\(f(Z)=\dfrac{1}{\sqrt{2\pi}}exp(-\dfrac{Z^2}{2})\) （下のグラフのY軸の値）

\(N\sim(0, \, 1)\)

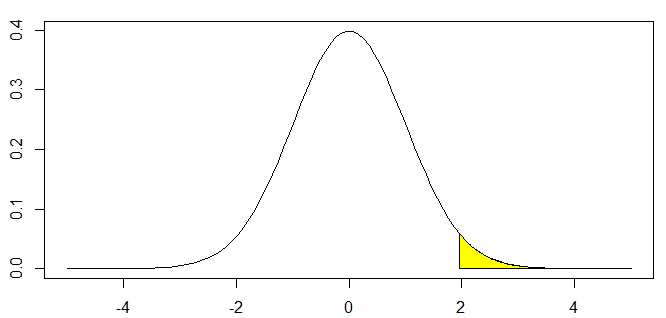
#グラフ
xseq <- seq(-5, 5,length=100)
plot(xseq, dnorm(xseq, 0, 1),type="l")

q = qnorm(0.025, lower.tail=F)
p <- seq(q, 5,length=100)
y <- dnorm(p, 0, 1)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="yellow")

黄色の部分が所謂P値になります（この一覧表が統計学の教科書の巻末によく記載されてます）

\(p値=1- \int_{-\infty}^{1.96}\frac{1}{\sqrt{2\pi}}exp(-\frac{Z^2}{2})dx\)

しかし簡単には標準正規分布に従う分布にはなりません

そこで中心極限定理や大数の法則などを理論として、正規分布に近似させた信頼区間などを算出します

95％信頼区間

\(Z=\dfrac{X-\mu}{\sigma}\) より \(\mu= X \pm Z \times \sigma\)