個別データを使用した感度・特異度とROC曲線の求め方
パッケージのインストール
R
# ==== 準備 ====
# 必要パッケージ
#packs <- c("readr", "dplyr", "pROC")
#to_install <- setdiff(packs, rownames(installed.packages()))
#if (length(to_install) > 0) install.packages(to_install, dependencies = TRUE)
library(readr)
library(dplyr)
library(pROC)pred には、ロジスティック回帰モデル fit2 が推定した「満足 = 1 になる確率(予測確率)」 が挿入される。これはアウトカム(満足)の発生確率をモデル化した値である。なお、ロジスティック回帰で 「暴露(介入)を受ける確率」 を推定した場合、その確率は 傾向スコア(propensity score) と呼ばれる。傾向スコアは因果推論で用いられる概念であり、本分析の「満足 = 1 の確率」とは目的が異なる。
R
dat2 <- dat2 %>%
mutate(pred = predict(fit2, type = "response"))感度・特異度を求める
例)カットオフ値を0.5に設定
R
cut_05 <- 0.5
tab_05<- table(
hat = factor(as.integer(dat2$pred >= cut_05), levels = c(1, 0)),
obs = factor(dat2$満足, levels = c(1, 0))
)
print(tab_05)
hat: 予測した満足「0と1」、obs: 実際の満足「0と1」
> print(tab_05)
obs
hat 1 0
1 35 9
0 14 42感度(Sensitivity):実際に満足だった(TP: True Positive, 真の陽性)人のうち、予測でも満足と判定できた割合。
# tab_05 は以下の形(行=予測, 列=真値)を前提:
# obs=1 obs=0
# hat=1 TP FP
# hat=0 FN TN
TP: True Positive
FP: False Positive
FN: False Negative
TN: True NegativeR
TP <- sum(dat2$満足 == 1 & dat2$pred >= cut_05)
FP <- sum(dat2$満足 == 0 & dat2$pred >= cut_05)
FN <- sum(dat2$満足 == 1 & dat2$pred < cut_05)
TN <- sum(dat2$満足 == 0 & dat2$pred < cut_05)
sensitivity <- TP / (TP + FN)
specificity <- TN / (TN + FP)
cat(sprintf("感度: %.3f\n特異度: %.3f\n", sensitivity, specificity))> cat(sprintf("感度: %.3f\n特異度: %.3f\n", sensitivity, specificity))
感度: 0.714
特異度: 0.824ROC曲線とAUC
注意:pROC::roc の response は {0,1}のベクトル、predictor はロジスティック回帰でもとめた連続変数(予測確率)です。
R
roc_obj <- roc(response = dat2$満足, predictor = dat2$pred, direction = "<")
#関数auc(): ROC曲線の下面積(Area Under the Curve = AUC)を計算する
auc_val <- auc(roc_obj)
#aucの95%CI
ci_auc <- ci.auc(roc_obj)
cat(sprintf("\nAUC: %.3f (95%%CI %.3f–%.3f)\n", auc_val, ci_auc[1], ci_auc[3]))Youden index で最適カットオフ
R
best <- coords(
roc_obj,
x = "best",
best.method = "youden",
ret = c("threshold", "sensitivity", "specificity", "ppv", "npv")
)
cat("\n--- Youden index での最適カットオフ ---\n")
print(best)
# 参考:最適カットオフでの混同行列
cut_best <- as.numeric(best["threshold"])
tab_best <- table(
obs = dat2$満足,
hat = as.integer(dat2$pred >= cut_best)
)
cat("\n最適カットオフでの混同行列:\n")
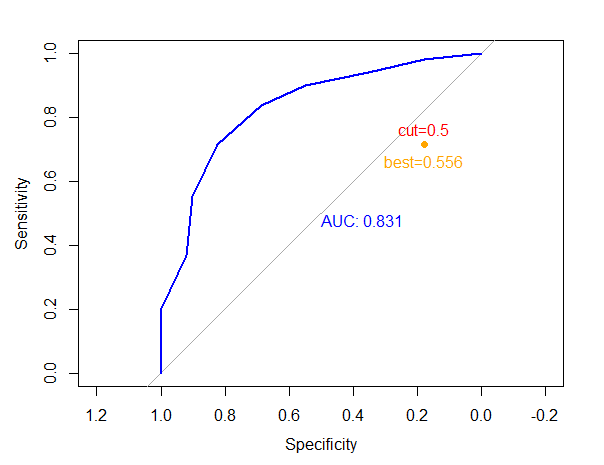
print(tab_best)ROC曲線の描画
R
plot(roc_obj, print.auc=TRUE, col="blue")
# カットオフ0.5
p05 <- coords(roc_obj, x=0.5, input="threshold",
ret=c("specificity","sensitivity"))
points(1 - p05["specificity"], p05["sensitivity"], pch=19, col="red")
text(1 - p05["specificity"], p05["sensitivity"] + 0.05, # ← 上にずらす
labels="cut=0.5", col="red")
# 最適カットオフ
best <- coords(roc_obj, x="best", best.method="youden",
ret=c("threshold","specificity","sensitivity"))
points(1 - best["specificity"], best["sensitivity"], pch=19, col="orange")
text(1 - best["specificity"], best["sensitivity"] - 0.05, # ← 下にずらす
labels=paste0("best=", round(best["threshold"],3)),
col="orange")