対応のあるt検定
3週目と6週目の差の検定を実行してみましょう(6週目-3週目)

これは対応のある2群の差の検定ですので、t検定で大丈夫です。ただし欠損しているデータが含まれているので、除外して検定しなければなりません。
欠損のある対象者3名(id=2, 12, 16)とperiod=bl を全て除外したデータセット yoko2 を作成
# Create a new dataset by excluding rows 12 and 16 from the data 'yoko'
yoko2 <- subset(
na.omit(yoko)
)
View(yoko2)
グラフ作成
横のデータになっているので、縦のデータの変換します。また、w3とw6を比較するグラフを作図します。
dat2 <- pivot_longer(
yoko2, cols = c("w3", "w6"),
names_to = "period",
values_to = "fim"
)
# Create a graph using dat2
g4 <- ggplot(dat2, aes(x = period, y = fim, group = id, colour = id)) +
geom_line() +
scale_x_discrete(
"Observation Points",
labels = c(
"w3" = "3 Weeks Later",
"w6" = "6 Weeks Later"
)
)
print(g4)今度は欠損値がないので、警告メッセージは表示されません。
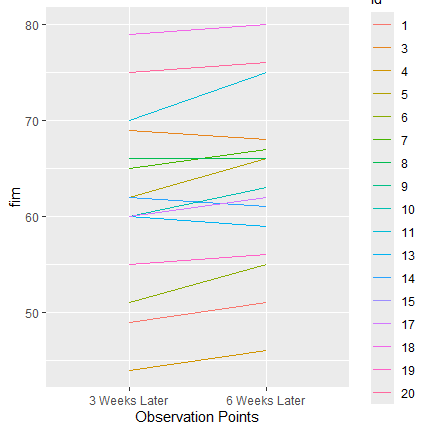
欠損値のある対象者3名を削除したので、全て関連性があります。これで通常の対応のあるt検定が実施できます。横のデータセット yoko から欠損のある対象者3名を除外したセット yoko2 を作成(n=18)。観測時点6週後と3週後のデータ間のt検定を実施。
t.test(yoko2$w6 - yoko2$w3)> t.test(yoko2$w6 - yoko2$w3)
One Sample t-test
data: yoko2$w6 - yoko2$w3
t = 3.9193, df = 16, p-value = 0.001223
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
0.7831843 2.6285804
sample estimates:
mean of x
1.705882 p<0.05で6週後のFIMが有意に高い結果となりました。しかし、この結果は欠損値のある3名を除いた17名のデータからの結果です。
混合効果モデル
反復測定分散分析(Repeated Measures ANOVA)と混合効果モデル
ANOVAにおいて、切片や傾きを被験者ごとに異なるランダム変数としてモデル化する場合、その分析は混合効果モデル(Mixed Effects Model)の一形態とみなされます。観測時点の効果を固定効果、各対象者の効果をランダム効果(変量効果)とした混合効果モデルを適用することで、各観測時点のデータの関連性を配慮した解析が可能となります。
例題を簡単なモデルにすると以下のようになります(簡単のためstageのランダム効果は除く)
$Y_{ij}=\mu+\pi_i+\gamma_j+b_i+\varepsilon_{ij}$
$i=1,…,n_j \quad j=bl, w3, w6$
$n_{bl}=20,\, n_{w3}=19, \, n_{w6}=18$
$\mu:$ 母平均
$\pi_i: $ 対象者 $i$ が属する群の効果(この例では stage や age の固定効果)
$\gamma_j:$ 時期の固定効果 $\quad$ j=bl (ベースライン),$\,$ j=w3 (3週間後),$\,$ j=w6 (6週間後)
$b_i: $ 対象者 $i$ の変量効果(各対象者 $i$ のばらつき) $\quad \sim N(0,\, \sigma_{id}^2)$
$\varepsilon_{ij}:$ 誤差(各対象者 $i$ の各観測時点 $j$ における効果) $\quad \sim N(0,\, \sigma_e^2)$

通常の線形回帰モデルは、固定効果のパラメータ($\mu, \pi_i, \gamma_j, \varepsilon_{ij}$)のみを推定するために使用されます。このモデルでは、対象者の効果を表すランダム効果 $b_i$(または変量効果)が正規分布を仮定した確率分布としてモデル化されます。固定効果とランダム効果の両パラメータを推定するために、混合効果モデルと称されます。
混合効果モデルによる対応のある2群の比較
欠損値をカットしたデータセット dat2 を使用
対象者のデータが反復して測定されているので、対象者をランダム効果(変量効果)としてモデルに投入します。
# lmer関数を使用した線形混合効果モデルによる解析
fit1 <- lmer(
fim ~ period + (1 | id), # (1 | id) これで対象者をランダム効果として指定
data = dat2
)
# モデルの要約を表示
summary(fit1)固定効果の結果に着目します。periodw6 の Estimate は 6w と 3w 差の平均値を示し、p値は上述した検定結果と同じ値を示しています。
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 76.63 8.754
Residual 1.61 1.269
Number of obs: 34, groups: id, 17
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 61.5882 2.1453 16.3327 28.709 2.07e-15 ***
periodw6 1.7059 0.4353 16.0000 3.919 0.00122 ** 欠損のある対象者も含めて解析
混合効果モデルを利用することで、欠損のある対象者も含めた解析が可能になります。データセット dat の period=3w, 6w を抜き出したデータセット(dat3)を使用します。
# Create dataset dat3 from dat excluding 'bl' (Baseline)
dat3 <- subset(dat, dat$period != "bl")
summary(dat3)> summary(dat3)
id age stage period fim
1 : 2 Min. :69.00 IV:14 bl: 0 Min. :44.00
2 : 2 1st Qu.:75.00 V :16 w3:20 1st Qu.:60.00
3 : 2 Median :77.00 VI:10 w6:20 Median :62.00
4 : 2 Mean :78.05 Mean :62.89
5 : 2 3rd Qu.:82.00 3rd Qu.:68.00
6 : 2 Max. :85.00 Max. :80.00
(Other):28 NA's :3 混合効果モデル
# Analyze with mixed-effects model using the lmer function
fit2 <- lmer(
fim ~ period + (1 | id),
data = dat3
)
# Display the model summary
summary(fit2)欠損値のあるデータを除外した場合とはやや異なる結果となります
Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 71.600 8.462
Residual 1.609 1.268
Number of obs: 37, groups: id, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 62.3746 1.9179 19.5663 32.523 < 2e-16 ***
periodw6 1.7010 0.4346 16.0887 3.914 0.00123 ** 欠損データには「Missing Completely at Random (MCAR)」、「Missing at Random (MAR)」、そして「Missing Not at Random (MNAR)」の三つの異なるタイプがあります。混合効果モデルを含む統計モデルを採用する際は、これらの欠損データの性質を理解し、それに応じた適切な対策を講じる必要があります。特に、「Missing Not at Random (MNAR)」の場合は、データの欠損が分析結果に大きなバイアスをもたらす可能性があるため、特に注意が必要です。MNARの状況では、データの欠損理由を詳細に調査し、可能であればその影響を緩和するための特別な統計手法を適用することが推奨されます。
経時データの相関
経時データの解析では、同じ対象者を異なる時点で測定するため、時点間の測定値が相関を持つことが一般的です。特に、ベースライン時点の個体間差が大きい場合、その個体の特性が後の時点の測定値にも影響を及ぼし、時点間の相関(serial correlation)が生じます。この相関を考慮せずに解析を行うと、標準誤差(SE)の推定が過大または過小に評価される可能性があり、統計検定の精度が低下します。また、固定効果の推定値が過大評価または過小評価される可能性があり、結果の解釈に影響を与えることがあります。
散布データの関連を確認します。yokoデータセットから”bl”, “w3”, “w6″の列を選択します。
pairs(
yoko[, c("bl", "w3", "w6")],
upper.panel = NULL
)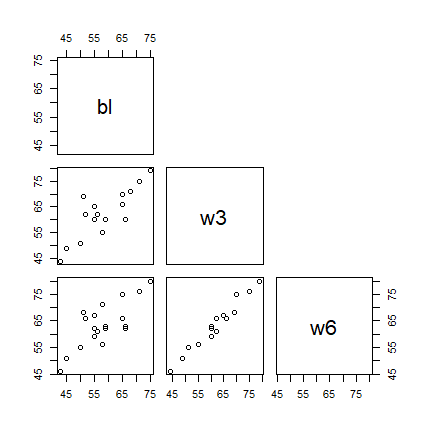
欠損しているデータを除いた yoko2 を使用して、分散・共分散行列と相関行例を表示します。
# Variance-covariance matrix
cov(yoko2[,c("bl", "w3", "w6")])
# Correlation matrix
cor(yoko2[,c("bl", "w3", "w6")])> # Variance-covariance matrix
> cov(yoko2[,c("bl", "w3", "w6")])
bl w3 w6
bl 78.68382 61.83824 61.48162
w3 61.83824 79.75735 76.62868
w6 61.48162 76.62868 76.72059
> # Correlation matrix
> cor(yoko2[,c("bl", "w3", "w6")])
bl w3 w6
bl 1.0000000 0.7806008 0.7913099
w3 0.7806008 1.0000000 0.9796028
w6 0.7913099 0.9796028 1.0000000切片モデル(ランダム切片モデル)
対象者ごとのランダム効果の切片の変動を取り入れて、そのばらつき(分散)を定量化するモデルです。このモデルでは、IDをランダム効果とすることで、各時点の各個人のばらつき(個体内変動)と個人間のばらつき(個体間変動)の両方を考慮することになります。 しかし、この設定では「時点間の相関」は完全にはモデル化されていません。
# Create a linear mixed-effects model using the lmerTest package
model1 <- lmerTest::lmer(
fim ~ period + (1 | id), # Define fixed and random effects
data = dat # Specify the dataset
)
# Display the model summary
summary(model1)Random effects:
Groups Name Variance Std.Dev.
id (Intercept) 60.85 7.801
Residual 11.63 3.411
Number of obs: 57, groups: id, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 58.600 1.904 23.537 30.782 < 2e-16 ***
periodw3 3.629 1.121 35.245 3.237 0.00263 **
periodw6 5.468 1.099 35.166 4.975 1.71e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Correlation of Fixed Effects:
(Intr) perdw3
periodw3 -0.272
periodw6 -0.278 0.470Random effects の Variance:ランダム効果の切片の分散:$\hat{\sigma}_{id}^2=61.04$(母分散を推定した分散)。Correlation of Fixed Effects (固定効果パラメータの相関行列);固定効果のパラメータが互いにどの程度関連しているかを示す。
3週目とblおよび6週目とblには差があることが理解できます。3Wと6Wの比較は基準カテゴリーを変更するか、多重比較で検定可能です。
model1から分散分析表の算出も可能です。
anova(model1)> anova(model1)
Type III Analysis of Variance Table with Satterthwaite's method
Sum Sq Mean Sq NumDF DenDF F value Pr(>F)
period 299.98 149.99 2 35.248 12.894 6.274e-05 ***固定効果パラメータの分散共分散行列を取得、標準偏差を計算、相関行列を計算
# Obtain the variance-covariance matrix of fixed effect parameters
cov_mod <- vcov(model1)
# Calculate standard deviations
std_mod <- sqrt(diag(cov_mod))
# Compute the correlation matrix
cor_mod <- cov_mod / (std_mod %o% std_mod)
# Print the correlation matrix
print(cor_mod)> print(cor_mod)
3 x 3 Matrix of class "dsyMatrix"
(Intercept) periodw3 periodw6
(Intercept) 1.0000000 -0.2724540 -0.2779912
periodw3 -0.2724540 1.0000000 0.4700948
periodw6 -0.2779912 0.4700948 1.0000000解釈(Intercept=bl)
bl vs w3 (-0.272): ベースラインが高いほど w3 の改善が少ない傾向
bl vs w6 (-0.278) :ベースラインが高いほど w6 の改善が少ない傾向
w3 vs w6 (0.470) :w3 での改善が大きい人は、w6 でも改善が大きい傾向

混合効果モデルの分散や相関行列の導出、またパラメータの推定や標準偏差の導出(Kenward-Roger、Satterthwaite)については、またの機会にアップしたいと思います。以下、ChatGPTの答えです。


切片・傾きモデル(ランダム切片、ランダム傾きモデル)
注意)
傾きを評価するためにperiodを連続変数として扱います(連続変数period_nを追加)。ベースラインを0、3週目を3、6週目を6と設定します。
library(dplyr)
dat <- dat %>%
mutate(period_n = case_when(
period == "bl" ~ 0,
period == "w3" ~ 3,
period == "w6" ~ 6,
TRUE ~ NA_real_
))「ランダム切片(random intercept)+ ランダム傾き(random slope)」のモデル。このモデルでは、個人内変動、個人間変動に加えて、時点間の相関をスロープ(傾き)として考慮します。ランダムスロープを導入することで、個人ごとの「時点ごとの変化率」の違いを反映し、より適切な推定が可能になります。
model2 <- lmerTest::lmer(
fim ~ period_n + (1 + period_n| id),
data = dat
)
summary(model2)(1 + period_n| id)
id : 個人ごとに異なる要素
1 + = ランダム切片モデル
0 + period_n : ランダム傾きモデル(ランダムスロープモデル)
1 + period_n : ランダム切片 + ランダム傾きモデル
Random effects:
Groups Name Variance Std.Dev. Corr
id (Intercept) 61.6225 7.8500
period_n 0.4814 0.6938 -0.11
Residual 7.1356 2.6713
Number of obs: 57, groups: id, 20
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 58.8635 1.8400 19.0576 31.991 < 2e-16 ***
period_n 0.9190 0.2126 19.1531 4.324 0.00036 ***多重比較
periodに有意な効果を認めたのでmodel1の多重比較を行います。
mc <- multcomp::glht(
model1,
linfct = mcp(period = "Tukey")
)
summary(mc)Linear Hypotheses:
Estimate Std. Error z value Pr(>|z|)
w3 - bl == 0 3.629 1.121 3.237 0.00342 **
w6 - bl == 0 5.468 1.099 4.975 < 1e-04 ***
w6 - w3 == 0 1.839 1.143 1.609 0.24193 調整(bonferroni)
summary(mc, test = adjusted("bonferroni"))Linear Hypotheses:
Estimate Std. Error z value Pr(>|z|)
w3 - bl == 0 3.629 1.121 3.237 0.00363 **
w6 - bl == 0 5.468 1.099 4.975 1.95e-06 ***
w6 - w3 == 0 1.839 1.143 1.609 0.32316
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Adjusted p values reported -- bonferroni method)次の調整が可能。”single-step”, “Shaffer”, “Westfall”, “free”, “holm”, “hochberg”, “hommel”, “bonferroni”, “BH”, “BY”, “fdr”, “none”

