超幾何分布

＊本サイトのサンプルデータは全て架空のものです

超幾何分布

超幾何分布は、有限個の要素から成る母集団より無作為に抽出したサンプルにおいて、特定の属性を持つ要素が何個含まれているかを示す確率変数の分布です。例えば、赤玉と白玉が混在する袋から無作為に玉をいくつか取り出す場合、取り出された赤玉の数の確率を求めるのに適用できます。Fisherの正確確率検定やログランク検定などで利用されている確率分布です。

データの準備と要約
超幾何分布
Rのdhyper関数
非復元抽出法（袋から取り出した玉は、袋に戻さない）
おまけ）復元抽出法

データの準備と要約

Fisherの正確確率検定で使用している以下の分割表（クロス表）をサンプルにします

仮想例題）29名（重度群15名、軽度群14名）の患者に対して治療Aを実施した。効果があったのは18例で、その中の重症群は12例であった。

この例をクロス表にすると以下のようになります

.libPaths("C:\\Users\\yyoshida\\Documents\\Rpackages")
cross1 <- matrix(c(12, 6, 18, 3, 8, 11, 15, 14, 29), ncol = 3)
colnames(cross1) <- c("効果あり", "効果なし", "計")
rownames(cross1) <- c("重度群", "軽度群", "計")
#View(cross1)

上記の例を一般化します

対象者数： $N$ 人

対象者の内訳：重度群 $M$ 人、軽度群 $N-M$ 人

全体の効果：治療Aの効果あり $k$ 人

重度群の効果：重度群のなかで治療Aの効果があった人数 $x$ 人

cross2 <- matrix(c(
  "x", "k-x", "k",
  "", "", "",
  "M", "N-M", "N"), 
  ncol = 3)
colnames(cross2) <- c("効果あり", "効果なし", "計")
rownames(cross2) <- c("重度群", "軽度群", "計")
#View(cross2)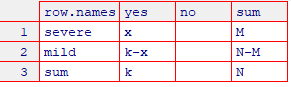

超幾何分布は、3つのパラメーター、$N$（全体の数）、$M$（特定の特徴を持つ要素の数）、$k$（抽出されるサンプルのサイズ）に基づきます。確率変数$X$は、「$k$回の抽出で得られた特定の特徴を持つ要素の数（$x$）」を表します。このような場合、$X$が従う分布を超幾何分布といいます。

$M, N, k$ が分かると周辺和がすべて固定され、さらに4つのセルのなかの1つ（$x$）を決めることで他のセルが全部決まります（自由度=1）

超幾何分布の確率関数

超幾何分布の確率関数は、このような特定の条件下での組み合わせ $(C=combination)$の確率として表されます

確率関数： $P(X=x) = \dfrac{_{M}C_{x}\times_{N-M}C_{k-x}}{_NC_k}$

$P(X=x)=\dfrac{( M 人から x 人を選択)( N-M から k-x 人を選択)}{全体 N 人から k 人を選択}$

確率変数$X$が超幾何分布に従っている場合の $X$ の期待値 $E(X)$ と分散 $V(X)$

期待値：$E(X) = k\dfrac{M}{N}$

分散：$V(X) = k\dfrac{M(N-M)}{N^2}\dfrac{N-k}{N-1}$

Rのdhyper関数

治療Aを受けた29名の例は以下のようになります（再掲）

$P(X=12)=\dfrac{_{15}C_{12}\times_{14}C_{6}}{_{29}C_{18}}=0.03949341$

組み合わせの数を求めるRの関数 choose を使用して次のように書くことができます

choose(15, 12)*choose(14, 6)/choose(29, 18)

関数 dhyper を使用して、もっと簡単に書くことができます

$P(X=ｘ)=$ dhyper(x, m, n, k)

dhyper(x=12, m=15, n=14, k=18)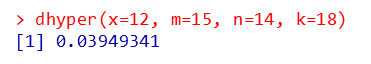

Rの関数 dhyper(x, m, n, k) のパラメータ標記に合わせたら以下のようになります

Rのdhyperは、通常の超幾何分布のパラメーター表記とは異なりますので注意が必要です

(m = M, n = N-M)

x : 赤玉が抽選される量子（quantiles）を表すベクトルです. 袋から置き換えなしで赤玉が引かれることを意味します。（非復元抽出法）

m : 袋の中の赤玉の総数

n : 袋の中の白玉の総数

k : 袋から取り出された玉の総数. この数は0からm+nまでの範囲でなければなりません. つまり、抽選される玉の数は袋の中の玉の総数を超えることはできません.

R: The Hypergeometric Distribution を一部改変

超幾何分布の確率関数グラフ

$P(X)$が従う分布を超幾何分布といいます

ここの例では重度群の人数は15名なので、$x$ の範囲は $0～15$ となります

どのような分布になるか見てみましょう

library(ggplot2)
# データの生成
x <- 0:15
p <- dhyper(x, 15, 14, 18)
# データフレームの作成
df1 <- data.frame(x, p)
# ggplotを使ったグラフの描画
ggplot(df1, aes(x = x, y = p)) +
  geom_bar(stat = "identity", fill = "skyblue", color = "black") +
  theme_minimal() +  # シンプルでモダンなテーマの適用
  labs(x = "x", y = "Probability", title = "超幾何分布") +
  geom_point(size = 3, color = "red") +  # データポイントを強調
  geom_line(aes(group = 1), color = "red")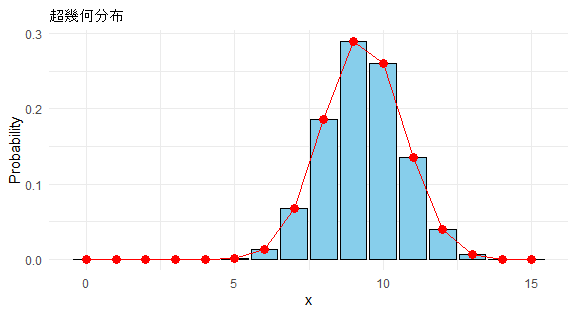

$x$ が12、13、14、15のときの確率を足せば片側検定のP値となります

x が12以上になる確率が小さい値になれば、偶然に起こったことと言えなくなります。なので、効果の割合に差があると言えるのです。

超幾何分布を使用した検定

例題：有意水準5%の片側検定の例

帰無仮説：重症群と軽症群では効果の割合に差がない

対立仮説：軽症群より重症群の方が効果ありの割合が多い（片側検定）

$P(X=12)$+$P(X=13)$+$P(X=14)$+$P(X=15)$を求めてみましょう

x <- 12:15
sum(dhyper(x, 15, 14, 18))

p値<0.05なので、「軽症群より重症群の方が効果ありの割合が有意に多い」という結果になります

Fisherの正確検定は超幾何分布を使っているので同じP値が算出されます

cross3 <- matrix(c(12, 6, 3, 8), ncol = 2)#分割表の作成
View(cross3)
fisher.test(cross3, alternative = "greater")$p.value

非復元抽出法（袋から取り出した玉は、袋に戻さない）

超幾何分布は、非復元抽出を前提としています。上述した治療効果の例ではイメージしずらいので赤玉と白玉を使って説明してみます！

ここまで治療Aの効果で説明してきましたが、統計学のテキストでは赤玉と白玉の例がよく紹介されています

赤玉と白玉が混在する袋から無作為に取り出したサンプルの中に含まれる赤玉の数の確率を調べる際に、超幾何分布を用いることができます

超幾何分布は、非復元抽出法で採取されたサンプルの確率分布です（1つずつ袋から取り出し、取り出した玉は袋に戻しません）

N個の玉（赤玉：M個、白玉：N-M個）入っている袋から非復元抽出法で取り出した$k$ 個の中に含まれる赤玉の数を $x$ 個とします

そして、その赤玉 $x$ の数を確率変数 $X$ とみなした場合、$X$ の分布は超幾何分布に従います

cross4 <- matrix(c(
  "x", "k-x", "k",
  "", "", "",
  "M", "N-M", "N"), 
  ncol = 3)
colnames(cross4) <- c("取り出した玉", "袋に残った玉", "計")
rownames(cross4) <- c("赤玉", "白玉", "計")
#View(cross4)