自由度$k$の$\chi^2$分布
ｶｲ二乗分布の前にガンマ分布をご参照ください
\(Z_1, Z_2, …, Z_k\) が独立に \(N(0, 1)\) に従う確率変数とする
$χ^2=\sum_{i=1}^k{Z_i^2}$
が従う確率分布を自由度\(k\)の\(χ^2\)分布とよび、\(χ^2(k)\)と標記する
確率密度関数： \(f(x;k)=\frac{1}{2^{\frac{k}{2}}Γ({\frac{k}{2}})}e^{\frac{-x}{2}}x^{\frac{k-2}{2}}\)
- \(Γ()\)はガンマ関数
期待値： \(E[χ^2]=k\)
分散： \(V[χ^2]=2k\)
\(χ_α^2(k)\)：上側確率\(100α％\)のパーセント点
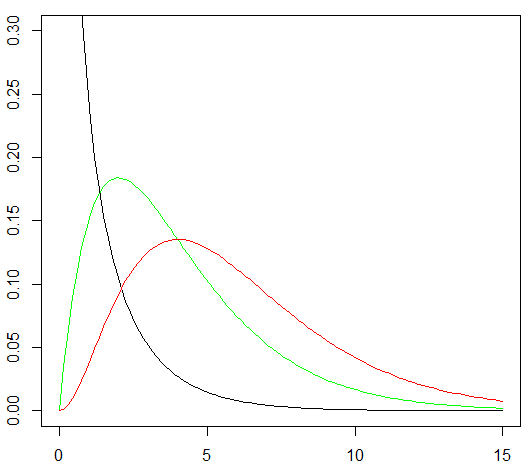
ｶｲ二乗分布は自由度によって形状が大きく異なる
自由度1, 3, 5のｶｲ二乗分布
curve(dchisq(x, 1), 0, 15, ylim=c(0,0.3)) #自由度1 赤
curve(dchisq(x, 4), 0, 15,col = "green", add = TRUE) #自由度3 緑
curve(dchisq(x, 6), 0, 15,col = "red",add = TRUE) #自由度5 青
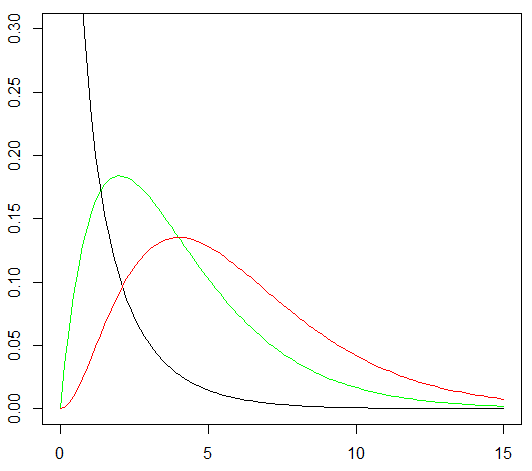
ガンマ分布の確率密度関数からｶｲ二乗分布は描けます
\(Ga(\dfrac{k}{2}, \dfrac{1}{2})\)は、自由度 \(k\) のｶｲ二乗分布
curve(dgamma(x , shape = 0.5, scale = 2) ,0 ,15, ylim=c(0,0.3))
curve(dgamma(x , shape = 2, scale = 2) ,0 ,15 ,add = T, col = "green")
curve(dgamma(x , shape = 3, scale = 2) ,0 ,15 ,add = T, col = "red")
ｶｲ二乗分布の性質
1, ｶｲ二乗分布の再生性
確率変数\(X_a, X_b\)が独立に \(χ^2(k_1)\)、\(χ^2(k_2)\)に従う場合
\(X_a + X_b\)は\(χ^2(k_1 + k_2)\)に従う
2, 正規分布からの標本（母平均）
\(N(μ,σ^2)\)に従う母集団から無作為抽出された\(X_i=X_1, X_2, …, X_n\)
\(\dfrac{X_i-μ}{σ}\)が\(N(0,1)\)に従うことから
\(W = \sum_{i=1}^{n}{\dfrac{(X_i – μ)^2}{σ^2}}\) は自由度\(n\)のｶｲ二乗分布に従う
3, 正規分布からの標本（標本平均）
\(\bar{X}=\dfrac{1}{n}\sum_{i=1}^{n}X_i\)の場合
\(W = \sum_{i=1}^{n}{\dfrac{(X_{i}-\bar{x})^2}{σ^2}}=\dfrac{(n-1)S^2}{σ^2}\)は自由度\(n-1\)のｶｲ二乗分布に従う
なぜならば、\(S^2 = \dfrac{1}{n-1}\sum_{i=1}^{n}{(X_{i}-\bar{X})^2}\)
3, Cochranの定理
独立な二つの標準正規分布の平方和 $W_1$、$W_2$ があった場合
$W_1=\sum_{i=1}^{k}X_i^2, \quad W_2=\sum_{i=k}^{k+l}X_i^2$
$W=W_1+W_2$ は自由度 $k+l$ の $\chi^2$ 分布に従う
コクランの定理は、特定の条件下で、総平方和（SST）が群間平方和（SSB）と誤差平方和（SSE）に分解され、これらが独立したカイ二乗分布に従うことを示します。ただし、この定理は主に分散分析（ANOVA）の文脈で用いられます。
例）
SST（総平方和） = SSB（群間平方和） + SSE（誤差平方和）
SSB は特定の自由度pのカイ二乗分布に従う
SSE は別の自由度qのカイ二乗分布に従う
SSB と SSE は独立
参考文献
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください