データの準備と要約

Fisherの正確検定、Fisherの正確確率検定、Fisherの直接確率検定、Fisherの直接法などと呼ばれています。ここでは、Fisherの正確確率検定をタイトルとして使用します。
新たなトレーニング方法が開発され、運動障害を持つ患者(重度群、軽度群)に対して実施された。軽度群と比較して、重度群の新トレーニング法の効果について有意水準5%で検証する。
仮説
障害レベル:重度(severe)、軽度(mild)
トレーニング効果:効果あり(yes)、効果なし(no)
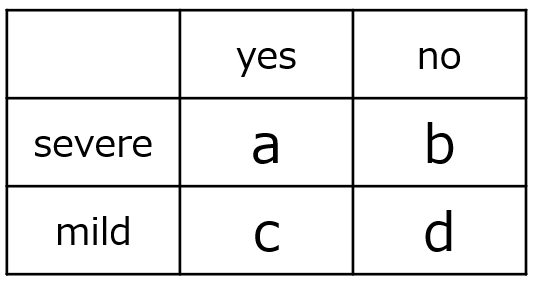
2×2の分割表において、「群間に独立性がある」という帰無仮説は、統計的には「オッズ比 = 1」と同義です。つまり、群1と群2で効果の割合が同じであるならば、オッズ比は1になります。ここでは、Fisherの正確確率検定の仮説を定式化するために、オッズ比という指標を用いて説明します。ただし、p値を求める際には、オッズ比そのものが直接使われるわけではありません。Fisherの検定では、固定された周辺度数のもとで各分割表が生じる確率に基づいてp値が計算されます。そのため、オッズ比が同じでも、分割表の構成や周辺度数によってp値が異なる場合があります。
オッズの定義
研究目的に応じてオッズとオッズ比を定義しなければなりません。また、解釈ミスが起こらないように分割表のルールを設定しておくことをおすすめします。ここでは、2×2分割表において、左上セル(重度群、効果あり)を基準にします。オッズの分子は効果あり、オッズ比の分子は重度群のオッズとなります。すなわち、オッズ比を分割表の (a/b)/(c/d) = ad/bc と定義します。
$オッズ=\dfrac{効果あり}{効果なし}$
$オッズ比=\dfrac{重度群のオッズ}{軽度群のオッズ}$
仮説
帰無仮説 H0: オッズ比=1(重度群のオッズ = 軽度群のオッズ)
対立仮説1 H1: オッズ比 > 1(重度群のオッズ > 軽度群のオッズ)➡ 上側検定
対立仮説2 H1: オッズ比 < 1(重度群のオッズ < 軽度群のオッズ)➡ 下側検定
対立仮説3 H1: オッズ比 ≠1(重度群のオッズ ≠ 軽度群のオッズ)➡ 両側検定

例題の意図を考えると「対立仮説2」と「対立仮説3」は不要なのですが、備忘録として3つの仮説を取り上げて勉強します。
サンプル(架空のサンプルです)
障害レベル:重度(severe)、軽度(mild)
トレーニング効果:効果あり(yes)、効果なし(no)
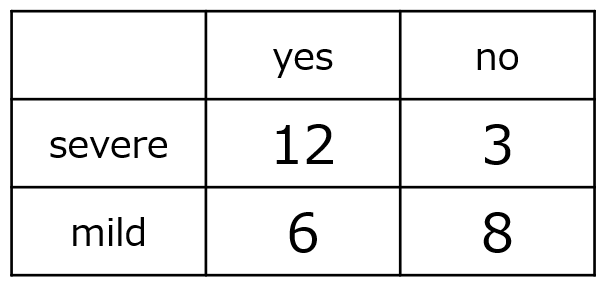
# Create the data
severity <- c(
rep("severe", 12),
rep("mild", 6),
rep("severe", 3),
rep("mild", 8)
)
severity <- factor(severity, levels = c("severe", "mild"))
effect <- c(rep("yes", 18), rep("no", 11))
effect <- factor(effect, levels = c("yes", "no"))
# Create a contingency table
tab <- xtabs(~ severity + effect)
# Display the result
print(tab)
> print(tab)
effect
severity yes no
severe 12 3
mild 6 8分割表をRで解析する場合、セルの順序や因子レベルの順序がこの定義に合っているかを確認することが重要です。Rでは、分割表の左上のセル(ここでは severe × yes)が基準になります。つまり、オッズの分子は「効果あり」となり、オッズ比の分子は「重度群」のオッズとなります。
$$\text{重度群のオッズ} = \frac{12}{3}=4$$
このオッズがオッズ比の分子となります。
$$\text{オッズ比} = \frac{12/3}{6/8} = \frac{12 \times 8}{3 \times 6} = \frac{96}{18}=5.33$$
このように、左上セルを基準にすることで、オッズ比の方向性(どちらの群に効果が高いか)を一貫して解釈できます。
factor() 関数は、名義変数をカテゴリカル変数(因子型変数)に変換するために使用されます。このとき、各カテゴリーは「水準(level)」として定義されます。levels() 関数を用いると、因子の水準が表示されますが、その中で最初に表示される水準が、統計モデルにおける基準カテゴリー(参照カテゴリー)として扱われます。これは、他のカテゴリーとの比較の基準点となるものです。基準カテゴリーは、relevel() 関数を使って明示的に変更することができます。また、factor() 関数の levels 引数を用いて水準の順序を指定することでも、基準カテゴリーを設定することが可能です。
確認してみます
levels(severity)
levels(effect)> levels(severity)
[1] "severe" "mild"
> levels(effect)
[1] "yes" "no" オッズ比は1より大きい結果となりました。オッズ比が高くなると重度群の効果割合が軽度群の効果割合より高いことを意味します。ただし、ここの効果割合とは、$\dfrac{効果あり}{効果なし}$ を指します。
パッケージのインストール
使用するパッケージ(パッケージのインストール)
library(exact2x2)分割表の操作については、以下の記事をご参照ください。
分割表の周辺合計
addmargins(tab)> addmargins(tab)
effect
severity yes no Sum
severe 12 3 15
mild 6 8 14
Sum 18 11 29周辺合計を固定した場合に、考えられる全ての分割表を求めます。
# Define a function to generate and display contingency tables
print_tables <- function() {
total_severe <- 15
total_mild <- 14
total_yes <- 18
total_no <- 11
# Calculate the possible range of values for a
# a corresponds to severe & yes
for (a in max(0, total_yes - total_mild):min(total_yes, total_severe)) {
b <- total_severe - a # severe & no
c <- total_yes - a # mild & yes
d <- total_no - b # mild & no
# Check if b, c, and d are all non-negative integers
if (b >= 0 && c >= 0 && d >= 0 && c <= total_mild && d <= total_mild) {
# Print only the contingency table
cat(sprintf("Effect\n"))
cat(sprintf("Severity Yes No\n"))
cat(sprintf("Severe %d %d\n", a, b))
cat(sprintf("Mild %d %d\n\n", c, d))
}
}
}
# Run the function to display all contingency tables
print_tables()> print_tables()
Effect
Severity Yes No
Severe 4 11
Mild 14 0
Effect
Severity Yes No
Severe 5 10
Mild 13 1
Effect
Severity Yes No
Severe 6 9
Mild 12 2
Effect
Severity Yes No
Severe 7 8
Mild 11 3
Effect
Severity Yes No
Severe 8 7
Mild 10 4
Effect
Severity Yes No
Severe 9 6
Mild 9 5
Effect
Severity Yes No
Severe 10 5
Mild 8 6
Effect
Severity Yes No
Severe 11 4
Mild 7 7
Effect
Severity Yes No
Severe 12 3
Mild 6 8
Effect
Severity Yes No
Severe 13 2
Mild 5 9
Effect
Severity Yes No
Severe 14 1
Mild 4 10
Effect
Severity Yes No
Severe 15 0
Mild 3 11考えられる分割表は12組あります。これでFisherの正確検定の準備は完了したので、有意水準5%で検定してみましょう。研究計画(何を立証したいのか)に従い、以下から適切な検定方法を選択します。
fisher.test()とexact2x2()

板垣様よりいただいたご意見をもとに修正しております。ありがとうございました。
オッズとオッズ比の定義を再確認します
$オッズ=\dfrac{効果あり}{効果なし}、オッズ比=\dfrac{重度群のオッズ}{軽度群のオッズ}$
片側検定(上側),alternative = “greater”
> addmargins(tab)
effect
severity yes no Sum
severe 12 3 15
mild 6 8 14
Sum 18 11 29対立仮説1 H₁: オッズ比 > 1(severe のオッズが mild のオッズよりも大きい)
この仮説を検証する際、Fisherの正確確率検定では、固定された周辺度数のもとで考えられるすべての 2×2 分割表の中から、観測された表と同様またはそれ以上にオッズ比が大きくなる表の確率を合計して、p値を算出します。これは、片側(上側)検定としての Fisher の正確検定の考え方に対応します。
次にRの関数でfisherの正確確率検定を実行してみましょう。上側検定の場合は、exact2x2 および fisher.test は同じ結果となります。
exact2x2(tab, alternative = "greater")fisher.test(tab, alternative = "greater")data: matrix(c(12, 6, 3, 8), ncol = 2)
p-value = 0.04601
alternative hypothesis: true odds ratio is greater than 1
95 percent confidence interval:
1.029929 Inf
sample estimates:
odds ratio
5.003853 X≧12、つまりX=12, 13, 14, 15 となる確率を求めます。
P(X) = P(X≧12 | severe=15, mild=14, yes=18 ) という条件付き確率になります。
P(X=12) + P(X=13) + P(X=14) + P(X=15)=0.046
この確率は超幾何分布を使って求めます(後で出てきます)。
この検定は、片側(上側)検定であり、対立仮説は「真のオッズ比は1より大きい」です。p値が 0.046(< 0.05)であるため、重症群と軽度群の間に有意差があると判断され、重症群のオッズが有意に高いと結論づけられます。
- p-value(p値)= 0.046
このP値は、超幾何分布に基づいて、観測された分割表以上に極端な表が出る確率を計算したものであり、Mid-P値(近似法)ではありません。 - alternative hypothesis(対立仮説): 上側検定の対立仮説は、「真のオッズ比は1より大きい」。p値<0.05なので「重症群のオッズは軽症群のオッズに比べて有意に高い」という結果になります。
- 95 percent confidence interval: 下記のオッズ比の95%信頼区間。
- オッズ比の推定値(5.003853)は、単純な割り算ではなく、条件付き最尤推定によって算出されています。詳細は奥村晴彦先生のページをご参照ください。
片側検定(下側),alternative = “less”
対立仮説2 H1: オッズ比 < 1(severe のオッズが mild のオッズよりも小さい)
この仮説を検証する際、Fisherの正確確率検定では、固定された周辺度数のもとで考えられるすべての 2×2 分割表の中から、観測された表と同様またはそれよりもオッズ比が小さくなる表の確率を合計して、p値を算出します。下側検定の場合は、exact2x2 および fisher.test は同じ結果となります。
exact2x2(tab, alternative = "less")fisher.test(tab, alternative = "less")data: matrix(c(12, 6, 3, 8), ncol = 2)
p-value = 0.9935
alternative hypothesis: true odds ratio is less than 1
95 percent confidence interval:
0.00000 29.77609
sample estimates:
odds ratio
5.003853 X≦12、つまり X=12, 11, 10, ・・・, 4 となる条件付き確率を求めます。
P(X≦12 | severe=15, mild=14, yes=18 )
=P(X=12) + P(X=11) + ・・・ + P(X=4)
=0.9935
p値は0.99なので帰無仮説が棄却できません。つまり、「severe グループのオッズが mild グループよりも低い」とは統計的には言えません。
両側検定, alternative = “two.sided”
対立仮説3 H1: オッズ比 ≠1(重度群のオッズ ≠ 軽度群のオッズ)
この仮説を検証する際、Fisherの正確確率検定では、固定された周辺度数のもとで考えられるすべての 2×2 分割表の中から、オッズ比が1より大きいか小さいかに関係なく、観測された表と同様に極端な表の確率を合計して、p値を算出します。これは、両側検定(alternative = "two.sided")としての Fisher の正確検定の考え方に対応します。なお、Fisherの検定はオッズ比そのものを直接用いるのではなく、各分割表が生じる確率に基づいて計算されますが、結果的にはオッズ比の大小に対応する傾向があります。
exact2x2関数との関係
このとき、exact2x2() 関数において tsmethod = "central" を指定することで、観測された分割表を中心とした「central p-value」を得ることができます。これは、両側検定においてより対称性を重視したp値の算出方法であり、fisher.test() の両側検定とは異なる結果になる場合があります(詳細は後述)。
code1(central)
exact2x2(tab, alternative = "two.sided", tsmethod = "central") Central Fisher's Exact Test
data: tab
p-value = 0.09203
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8163182 40.7244582
sample estimates:
odds ratio
5.003853 最小尤度によるp値を求める場合は、以下のようになります。(詳細は後述)
code2(minlike)
exact2x2(tab, alternative = "two.sided", tsmethod = "minlike")tsmethod = “minlike”はデフォルトの設定になっています
Two-sided Fisher's Exact Test (usual method using minimum likelihood)
data: tab
p-value = 0.06043
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8327 29.7621
sample estimates:
odds ratio
5.003853 以下も同じ方法でp値を算出します
code3(fisher.test)
fisher.test(tab, alternative = "two.sided") Fisher's Exact Test for Count Data
data: matrix(c(12, 6, 3, 8), ncol = 2)
p-value = 0.06043
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8163182 40.7244582
sample estimates:
odds ratio
5.003853
まとめ
| 式 | p値の定義 |
|---|---|
code1 (central) | central p-value |
code2 (minlike) | 最小尤度によるp値 |
code3 (fisher.test) | 最小尤度によるp値 |
Fisherの正確検定はノンパラメトリックな方法であり、標本分布の仮定を置かずに、固定された周辺度数のもとでの条件付き確率に基づいてP値を算出します。この検定では、オッズ比およびその信頼区間も併せて算出されることがありますが、これらは効果の大きさ(effect size)を補足的に示すものであり、P値による有意性検定とは異なる情報を提供します。