超幾何分布
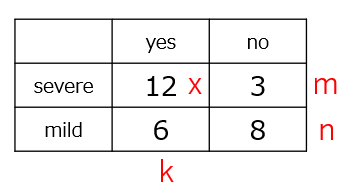
P(X | x=12, m=15, n=14, k=18) の条件付き確率は、超幾何分布から特定の成功数が抽出される確率を計算します。
上記の記事より確率を求めます
P(X=12)=$\dfrac{_{15}C_{12}\times_{14}C_{6}}{_{29}C_{18}}$=0.03949341
組合せの関数choose()を使用すると、以下のようになります
choose(15, 12)*choose(14, 6)/choose(29, 18)> choose(15, 12)*choose(14, 6)/choose(29, 18)
[1] 0.03949341Fisherの正確検定のp値の求め方
Rの関数を使用して、P(X | x=12, m=15, n=14, k=18) を求めます。dhyperは超幾何分布の確率質量を求める関数です(”d”は通常 “density” を意味しますが、ここでは離散分布の確率質量を指します)。
観測された分割表の周辺度数(行・列の合計)は固定です。その条件下で、起こりうるすべての分割表を列挙し、それぞれの表が出現する確率を計算します。この「起こりうる分割表の集合」を確率的な母集団とみなします。

dhyper関数のパラメータ説明(例題の数)
x : 成功が観測された回数(severe の中の yes の数)
m : 母集団の成功の数(severe の数)
n : 母集団の失敗の数(mild の数)
k : 抽出回数(yes の数)
*重度群に対する効果を検証するので、この例では、成功を”重度群”、また観察を”効果あり”として扱います。少し分かりにくいので、超幾何分布をご参照ください。
周辺合計(行・列の合計)を固定したときに、x=12になる確率を求めます。
x <- 12 # Observed number of successes
m <- 15 # Total number of successes in the population
n <- 14 # Total number of failures in the population
k <- 18 # Size of the sample to be drawn
dhyper(x, m, n, k)> dhyper(x, m, n, k)
[1] 0.03949341片側検定(上側),alternative = “greater” のp値
超幾何分布に基づく累積確率から求めるp値
exact2x2(tab, alternative = "greater")$p.valuefisher.test(tab, alternative = "greater")$p.value0.04601384sumは集計結果を算出する関数です。
x <- c(12:15)
m <- 15
n <- 14
k <- 18
sum(dhyper(x, m, n, k))> sum(dhyper(x, m, n, k))
[1] 0.04601384Rの関数
dhyper(x, m, n, k):指定されたxに対する超幾何分布の確率を返します。
phyper(q, m, n, k):累積分布関数。lower.tail = FALSEを指定すると、qより大きい値の確率の総和を返します。
x <- c(15:4)
m <- 15
n <- 14
k <- 18
d <- dhyper(x = x, m, n, k)
pu <- phyper(q = x - 1, m, n, k, lower.tail=FALSE)
pl <- phyper(q = x, m, n, k)
df <- data.frame(x, d, pu, pl)
round(df, 6)d: 超幾何分布の確率質量関数(各xに対する確率)
pu: 上側の累積確率(x以上の確率)
pl: 下側の累積確率(x以下の確率)
x d pu pl
1 15 0.000011 0.000011 1.000000
2 14 0.000434 0.000445 0.999989
3 13 0.006076 0.006520 0.999555
4 12 0.039493 0.046014 0.993480
5 11 0.135406 0.181420 0.953986
6 10 0.260657 0.442076 0.818580
7 9 0.289618 0.731695 0.557924
8 8 0.186183 0.917878 0.268305
9 7 0.067703 0.985581 0.082122
10 6 0.013164 0.998745 0.014419
11 5 0.001215 0.999961 0.001255
12 4 0.000039 1.000000 0.000039P(X≧12) = P(X=12) + P(X=13) + P(X=14) + P(X=15)

このように、p値を求める際には、オッズ比そのものが直接使われるわけではありません。オッズ比が同じでも、分割表の構成や周辺度数によってp値が異なる場合があります。オッズ比が6で、分割表の構成や周辺度数によってp値が異なる場合の例を示します。
tables <- list(
"Table 1" = matrix(c(8, 2, 4, 6), nrow = 2),
"Table 2" = matrix(c(16, 4, 8, 12), nrow = 2),
"Table 3" = matrix(c(4, 1, 2, 3), nrow = 2),
"Table 4" = matrix(c(40, 10, 20, 30), nrow = 2),
"Table 5" = matrix(c(80, 20, 40, 60), nrow = 2)
)
# Create a data frame to store the results
results <- data.frame(
Table = character(),
OddsRatio = numeric(),
PValue = numeric(),
stringsAsFactors = FALSE
)
# Perform Fisher's exact test (one-sided: greater) for each table
for (name in names(tables)) {
test <- fisher.test(tables[[name]], alternative = "greater")
results <- rbind(results, data.frame(
Table = name,
PValue = round(test$p.value, 4)
))
}
# Display the results
print(results)
Table PValue
1 Table 1 0.0849
2 Table 2 0.0112
3 Table 3 0.2619
4 Table 4 0.0000
5 Table 5 0.0000両側検定, alternative = “two.sided” のcentral-pvalue
固定された周辺度数のもとで、観測された分割表が得られる確率を超幾何分布に従って計算し、これをpとします。次に、そのp よりも確率が小さい(つまり、もっと“ありそうにない”)分割表を探します。ただし、オッズ比が観測値より大きい方向と小さい方向の両方を対象にします。つまり、観測された表を「中心」として、左右対称に極端な表を集めるイメージです。それらの「もっと極端な表」の確率をすべて足し合わせます。最後に、その合計を 2倍 したものが central p-value になります。
central p-valueの求め方(tsmethod = “central”)
exact2x2(tab, alternative = "two.sided", tsmethod = "central")$p.value0.09202767Xが観測値以上になる確率を合計(累積確率)。その合計を2倍した値が central p-value。
central p-value = 0.046014×2
d: 超幾何分布の確率質量関数(各xに対する確率)
pu: 上側の累積確率(x以上の確率(上側))
pl: 下側の累積確率(x以下の確率(下側))> round(df, 6)
x d pu pl
1 15 0.000011 0.000011 1.000000
2 14 0.000434 0.000445 0.999989
3 13 0.006076 0.006520 0.999555
4 12 0.039493 0.046014 0.993480
5 11 0.135406 0.181420 0.953986
6 10 0.260657 0.442076 0.818580
7 9 0.289618 0.731695 0.557924
8 8 0.186183 0.917878 0.268305
9 7 0.067703 0.985581 0.082122
10 6 0.013164 0.998745 0.014419
11 5 0.001215 0.999961 0.001255
12 4 0.000039 1.000000 0.000039両側検定, alternative = “two.sided” の最小尤度によるp値
exact2x2(tab, alternative = "two.sided", tsmethod = "minlike")(tsmethod = “minlike”はデフォルトなので書かなくてもよい)
Two-sided Fisher's Exact Test (usual method using minimum likelihood)
data: matrix(c(12, 6, 3, 8), ncol = 2)
p-value = 0.06043
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8327 29.7621fisher.test(tab, alternative = "two.sided")Fisher's Exact Test for Count Data
data: matrix(c(12, 6, 3, 8), ncol = 2)
p-value = 0.06043
alternative hypothesis: true odds ratio is not equal to 1
95 percent confidence interval:
0.8163182 40.7244582上の2つのコードは、どちらも同じ最小尤度によるp値を算出します。ただし、信頼区間の算出方法異は異なります。
x=12が観測される確率(0.03949341)よりも小さい確率を全て合計することで、最小尤度によるp値が求められます。
上側の累積確率:0.046014
下側の累積確率:0.014419
合計:0.046014+0.014419=0.060433
d: 超幾何分布の確率質量関数(各xに対する確率)
pu: 上側の累積確率(x以上の確率(上側))
pl: 下側の累積確率(x以下の確率(下側))
x d pu pl
1 15 0.000011 0.000011 1.000000
2 14 0.000434 0.000445 0.999989
3 13 0.006076 0.006520 0.999555
4 12 0.039493 0.046014 0.993480
5 11 0.135406 0.181420 0.953986
6 10 0.260657 0.442076 0.818580
7 9 0.289618 0.731695 0.557924
8 8 0.186183 0.917878 0.268305
9 7 0.067703 0.985581 0.082122
10 6 0.013164 0.998745 0.014419
11 5 0.001215 0.999961 0.001255
12 4 0.000039 1.000000 0.000039このように同じfisherの検定でも求め方によりp値が異なる場合がありるので、十分に注意してください。

黒木玄様(@genkuroki)よりご助言いただきました。ありがとうございました。


