対応のある一元配置分散分析、1要因ランダムブロックデザイン

通常行われている二元配置分散分析は、要因Aか要因Bのどちらかの効果を検証します。ここでは、理学療法の実施期間(要因A)が解析の対象となります。施設要因は、効果を検証することが目的ではなく、誤差を減らすために取り込みます。そのような場合には、施設A、B、C、D、Eはブロック因子となります。
もし施設A、B、C、D、Eを無視して、以下のように要因Bを誤差と見なせば、繰り返し測定と同じ扱いになり、一元配置分散分析の適応となります
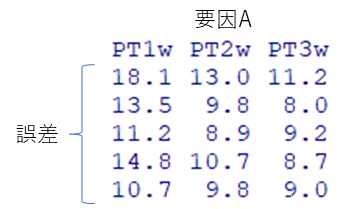
しかし今回の例題では、PT実施期間(1週間、2週間、3週間)である要因Aに加えて要因Bも結果に影響します
このような場合には、要因が2つあるので二元配置分散分析となります

したがって 全体の誤差(ばらつき)= 要因Aの効果 + 要因Bの効果 + 誤差 となります
要因Aの効果、要因Bの効果は主効果と呼ばれます
回帰分析(カテゴリカルデータ)
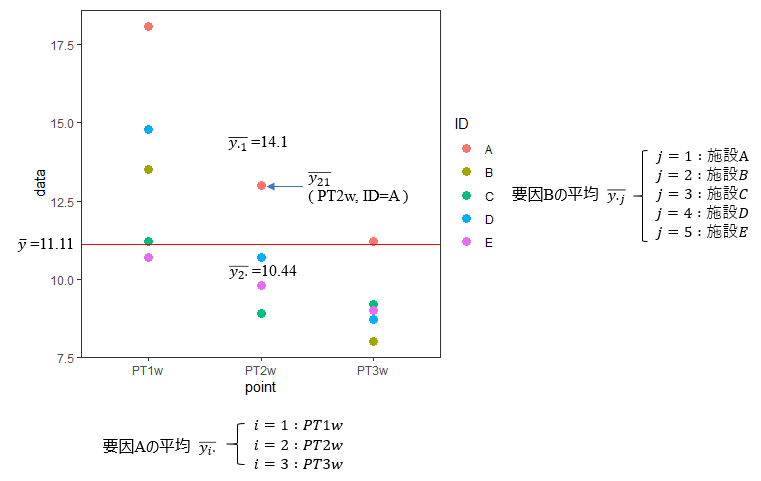
要因A間の差:PT1w(平均13.66)を基準として他の期間との差を求めてみます
- PT2wの平均ーPT1wの平均\(=10.44-13.66=-3.22\)
- PT3wの平均ーPT1wの平均\(=9.22-13.66=-4.44\)
要因B間の差:施設A(平均14.1)を基準として他の施設との差を求めてみます
- 施設Bの平均ー施設Aの平均\(=10.43-14.1=-3.67\)
- 施設Cの平均ー施設Aの平均\(=9.76-14.1=-4.34\)
- 施設Dの平均ー施設Aの平均\(=11.4-14.1=-2.7\)
- 施設Eの平均ー施設Aの平均\(=9.83-14.1=-4.27\)
2変数の重回帰分析を実行(ただし両変数とも名義変数)
fit <- lm(data ~ point + ID, data=dat2)
summary(fit)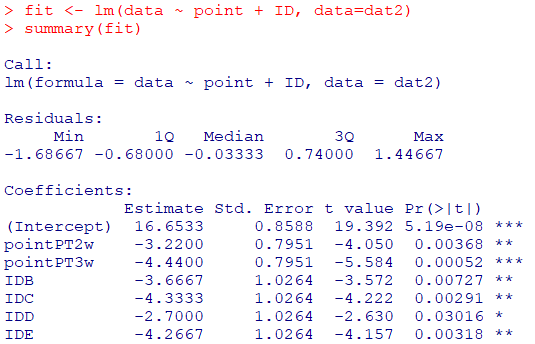

説明変数がカテゴリカルデータの場合には解釈に気を付けましょう
- 回帰分析の係数の推定値は、上で求めた要因A間の差、要因B間の差になります
- ここのF値は要因Aと要因Bの平方和の総和(自由度=2+4)から算出されています
- p<0.05となり両要因の効果があることが示されました
分散分析表
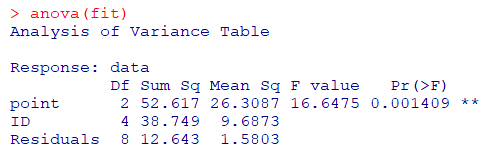
回帰分析の結果をanova関数に渡すことで分散分析表が算出されます
anova(fit)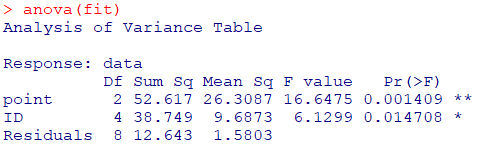
- このF値は要因Aと要因Bそれぞれの平均平方和から算出されます
- pointのp値<0.05なので、PTの実施期間の効果があることが言えます
- 要因Bはブロック因子となるので、分散分析表には以下のように要因Aの結果のみを記載します(当たり前ですが、結果は二元配置分散分析と全く同じものです)
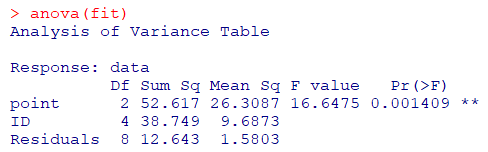
結果のみでよければ、ここまででOKです

ここからはもう少し詳しく勉強してみましょう
統計モデルと仮説

\( y_{ij}-\bar{y}=(\bar{y_{i\cdot}}-\bar{y})+(\bar{y_{\cdot j}}-\bar{y})+\)残差
残差=\(y_{ij}+\bar{y}-\bar{y_{i\cdot}}-\bar{y_{\cdot j}}\)
\( y_{ij}-\bar{y}=(\bar{y_{i\cdot}}-\bar{y})+(\bar{y_{\cdot j}}-\bar{y})+(y_{ij}+\bar{y}-\bar{y_{i\cdot}}-\bar{y_{\cdot j}})\)
二元配置分散分析の統計モデル
\(y_{ij}=\mu + \alpha_{i} + \beta_{j} + e_{ij}\)
\(\quad (i=1,2,3, \quad j=1,2,3,4,5)\)
\(\alpha_{i}:\)要因AのPT期間 \(i\) の効果
\(\beta_{j}:\)要因Bのブロック因子 \(j\) の効果
仮説
要因Aの効果を検証することが目的となるので、仮説は以下のようになります
帰無仮説A:要因Aの効果がない($\alpha_{1}=\alpha_{2}=\alpha_{3}=0$)
対立仮説:要因Aのいずれかに効果がある($\alpha_{1}, \alpha_{2}, \alpha_{3}$の少なくとも1つは0ではない)

理学療法期間とTUGの関連性を検証するためには多重比較が必要になります。ただし因果関係を証明したいのであれば、単に比較するだけでは不十分です。
残差
理学療法の実施期間にともなうTUGの変化が施設間で異なる(要因A×要因Bの交互作用がある)場合でも、その効果は残差 \(e_{ij}\)に含まれることになります

繰り返し測定のある二元配置分散分析のように交互作用と誤差項の分離ができないので、ここでは要因A×要因Bの交互作用を誤差とみなしています。つまり繰り返しのない二元配置分散分析では、たとえ要因A×要因Bの交互作用があったとしても誤差として捉えて、研究目的である要因Aの主効果を評価しているのです。

