二元配置分散分析（繰り返し測定あり）

分散分析表

fit <- lm(range ~ method*age, data=dat2)
anova(fit)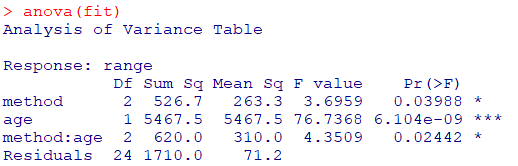

あるmethodには効果があり、またどちらかのageに効果があることが理解できます

また交互作用もあることから、特定のmethodと特定のageで効果があるようです

結果まででよければ、ここまででOKです

ここからもう少し詳しく勉強してみましょう

各層の平均値

全体の平均と11グループの平均値が必要になります

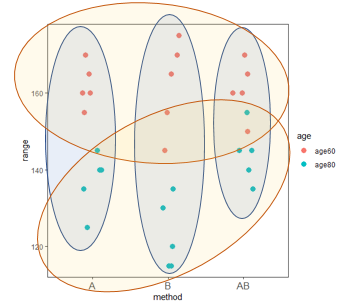
ageで層別、methodで層別

mean(dat3$range)
psych::describeBy(dat3$range,
    group = list(age = dat3$age)
) 
psych::describeBy(dat3$range,
    group = list(method = dat3$method)
) 

不要な値も含まれていますが、縦データの要約には、この方法が一番簡単なようです。他の方法があったらまた紹介します。

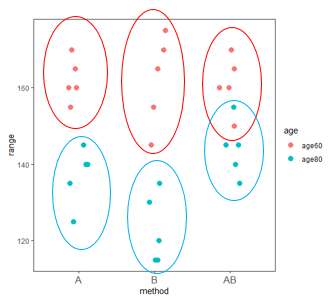
age✕methodで層別（6ブロック）

ここでは平均値だけを取り出してみましょう。

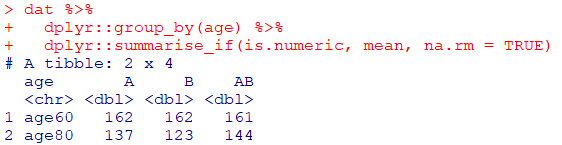
dat %>% 
  dplyr::group_by(age) %>% 
  dplyr::summarise_if(
    is.numeric, mean, na.rm = TRUE
  )

注意）dat→横データを使用しています

縦データのdat3を使うのであれば・・・

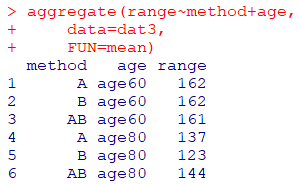
aggregate(
    range ~ method + age,
    data=dat3,
    FUN=mean
)

（ちょっと見にくいか・・・）

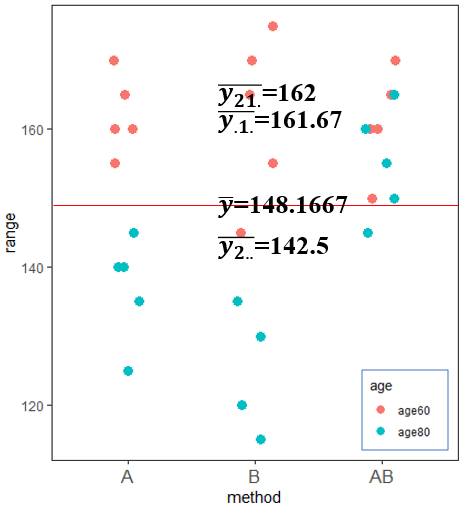
例）下のグラフには全体、60歳代、B群、60歳代Ｂ群の平均値を記載しています

統計モデル

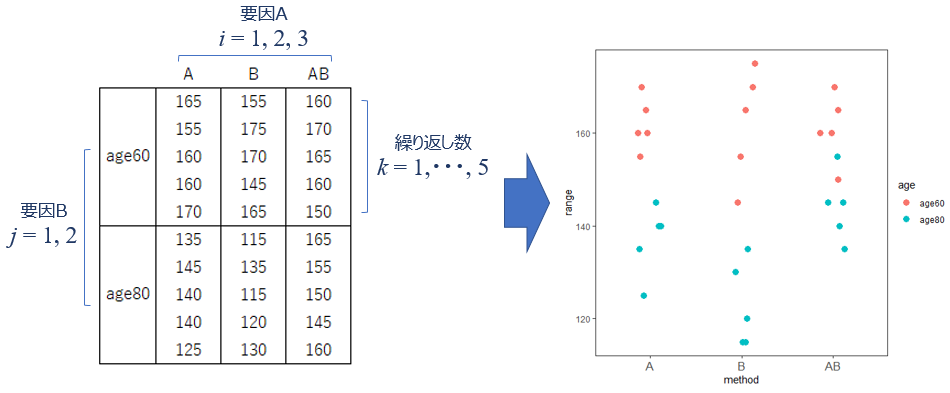
繰り返し測定のない二元配置分散分析とは異なり、ここでは交互作用の効果も検証します

\(y_{ijk}=\mu + \alpha_{i} + \beta_{j} + \alpha_{i}*\beta_{j}+ e_{ijk}\)
\(\quad (i=1,2,3 \quad j=1,2 \quad k=1,2, \cdots, 5)\)

$\quad \alpha_{i}=\bar{y_i..}-\bar{y}=$方法 A, B, AB の効果

$\quad \beta_{j}=\bar{y_{.j.}}-\bar{y}=$年齢の効果

$\quad \alpha_{i}*\beta_{j}=\bar{y_{ij.}}-\bar{y_{i..}}-\bar{y_{.j.}}+\bar{y}=$交互作用の効果

$\quad e_{ijk}=y_{ijk}-\bar{y_{ij.}}=$残りの効果（上述した効果では説明できない効果=各年齢、各方法の組み合わせた群内の残差）

以下のように書けます

\(y_{ijk} = \bar{y} + (\bar{y_i..}-\bar{y}) + (\bar{y_{.j.}}-\bar{y})+(\bar{y_{ij.}}-\bar{y_{i..}}-\bar{y_{.j.}}+\bar{y})+(y_{ijk}-\bar{y_{ij.}})\)

\((y_{ijk}-\bar{y}) = (\bar{y_i..}-\bar{y}) + (\bar{y_{.j.}}-\bar{y})+(\bar{y_{ij.}}-\bar{y_{i..}}-\bar{y_{.j.}}+\bar{y})+(y_{ijk}-\bar{y_{ij.}})\)