重回帰分析

残差分析

実測値 $y_i$ と回帰式から得られる値 $\hat{y_i}$ をプロットしてみましょう

#切片
b0 <- coef(fit)[1]
#BMI
b1 <- coef(fit)[2]
#前FIMmの係数
b2 <- coef(fit)[3]
#PT時間
b3 <- coef(fit)[4]

print(c(b0, b1, b2, b3))

FIM差の予測式から求めた予測値

yhat1 <-  b0 + b1*dat$BMI + b2*dat$前FIMm + b3*dat$PT時間

Rのpredict関数を使えば予測値を簡単に求めることができます

yhat2 <- predict(fit)
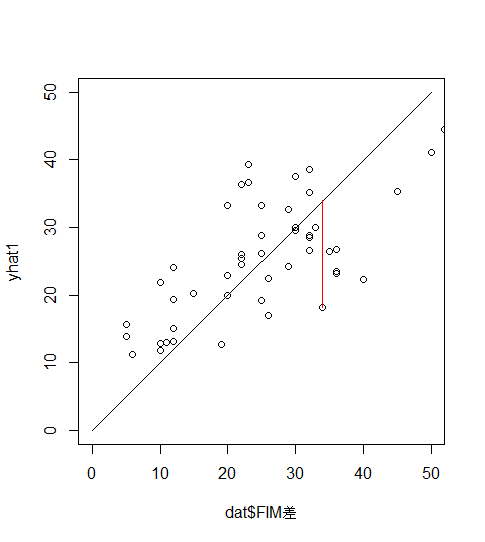
# yhat1 = yhat2

FIM差をx軸、FIM差の推定値をy軸にして、誤差を確認します

plot(dat$FIM差, yhat1, xlim = c(0, 50), ylim = c(0, 50))

# Y=Xの直線
segments(
    x0=0, y0=0, 
    x1=50, y1=50
)

#誤差の例
segments(
    x0=dat$FIM差[3], y0=yhat1[3], 
    x1=dat$FIM差[3], y1=dat$FIM差[3],
    col="red"
)

＊ yhat1 を yhat2 に変えても全く同じグラフになります

Y=Xの線上からのズレ（赤線）が誤差になります

Bland Altman Plotで確認してみます

ba <- BlandAltmanLeh::bland.altman.stats(
  dat$FIM差, yhat1
)  

#str(ba)で確認して必要な部分だけ抜き取ります
plot(
    ba$means, ba$diffs, 
    xlab="FIM差とyhat1の平均値",
    ylab="FIM差とyhat1との差"
)
abline(h=0, lty=2, col=2)

０を中心になんとなく正規分布しているようです

次に残差のヒストグラムを見てみます

hist(
    dat$FIM差-yhat1,
    main="残差",
    xlab="", ylab=""
)

正規分布の形状のようです

QQプロット

qqnorm(dat$FIM差-yhat1)
qqline(dat$FIM差-yhat1)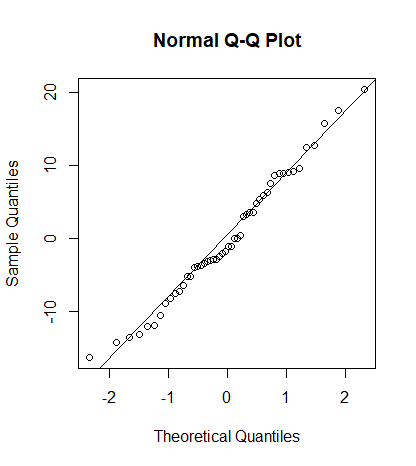

正規分布していることが確認できました

残差分析

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください

コメント欄『間違い』や『分かりにくい部分』などのご意見もお寄せください