ロジスティック回帰 (1)

ここからはもう少し詳しく学習しましょう

ロジット変換、ロジスティック変換（logistic transformation)

ロジット変換とは、確率 $\pi$ を $log\dfrac{\pi}{1-\pi}$ へ変換することです

この変換により、$0<\pi<1$ に対して、 $-\infty<log\dfrac{\pi}{1-\pi}<\infty$ となります

ロジット変換は、説明変数がどんな値をとっても予測値が0から1に収まるように目的変数を変換する方法です。0または1を目的変数とする統計的推測に柔軟性を持たせた方法と言えます。

① 満足と答える確率 $P$ のオッズを求めます

リハビリを1週間に$x_i$単位 受けた患者が満足と答える確率 $P$ のオッズを満足度オッズとします

満足度オッズ=$\dfrac{満足と答える確率}{1-満足と答える確率}=\dfrac{P(x_i)}{1-P(x_i)} \qquad (x_iはリハ単位数)$

② 満足度オッズを対数変換します（ロジット変換）

満足度オッズ $\dfrac{P(x_i)}{1-P(x_i)}$ の対数をとります（$0<P(x_i)<1$）

$logit(P)=log(\dfrac{P(x_i)}{1-P(x_i)})$

ロジスティック変換をする理由

$0<P<1$ の範囲で $-\infty<logit(P)<\infty$ となり、線形回帰（ $logit(P)=\beta_0+\beta_1x_i$ ）に置き換えることで、リハビリ単位数 $x_i$ がどのような値でも$0<P(x_i)<1$ の範囲に収まることになります

これで、単回帰のように予測式が0または1を突き抜けることはありません

ｘ軸が確率、y軸が $logit(P)$ のグラフからはシグモイド曲線になることが確認できます

y <- function(P){
    return(log(P/(1-P)))
    }

plot(y, xlab ="P", ylab = "logit(P)")
abline(0,0)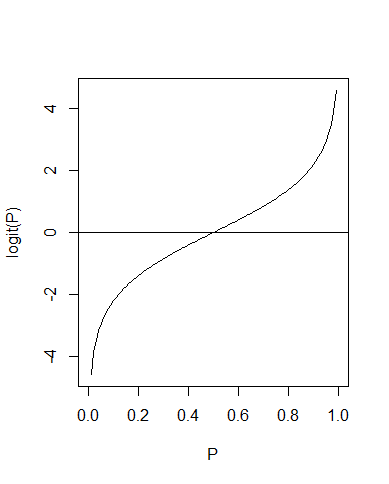

このシグモイド曲線を利用することで、リハビリを $x_i$時間 受けた患者が満足と答える確率 $P(x_i)$ を予測できそうですね！

ロジスティック回帰モデル

$logit(P) = \beta_0+\beta_1x_i$

＊ここでは、推定したいパラメタを $\beta_i$、推定の結果得られた係数を $b_i$ として区別します

$x_i$ がリハビリ単位数とすると、このモデルからパラメタを推定することで

$logit(\hat{P})=b_0+b_1*x_i$

のような予測式を立てることができます（$\hat{P}$は予測確率です）

family = binomial

今回の例では各単位ごとに上限があるカウントデータとなります。このような場合は二項分布を使用します（family = binomial）。上限がない場合にはポアソン分布を利用するとになります（family = poisson）。

link=”logit”

目的変数を $ax + b$ のような一次方程式（多変数もあり）に対応させるための関数をリンク関数と呼びます。今回の場合はロジット変換したので、リンク関数は ロジットリンク関数 $log(\dfrac{P}{1-P})$ です。Rでは link=”logit” と指定します。二項分布のデフォルトになっていますが、正確には以下のように書きます（もちろん答えは同じです）。

fit <- glm(
    cbind(満足, 患者数-満足) ~ 単位数, 
    family=binomial (link="logit"), 
    data=dat
)

cbind(満足, 患者数-満足)の2列を link=”logit” でロジット変換して、確率分布は family = binomial で二項分布を指定して尤度を求める・・・という式になります

モデル

$logit(P) =log(\dfrac{P}{1-P})=\beta_0 + \beta_1x_i$

$P=$満足と回答する確率,   $x_i=$単位数

$P$ について解くと以下のようになります

$P=\dfrac{e^{\beta_0 + \beta_1x_i}}{1 + e^{\beta_0 + \beta_1x_i}}$　（変数 $x_i$ が多い場合、傾向スコアとして使用される値です）

グラフ

ロジスティック回帰の結果から $b_0$ と $b_1$ が推定されたので、上記の式に当てはめてｘ軸を「リハビリ単位数」、ｙ軸を「満足と回答する確率$\hat{P}$」とした予測曲線を描くことができます

#x軸の範囲
x <- seq(0, 60)
#切片
b0 <- coef(fit)[1]
#回帰係数
b1 <- coef(fit)[2]
#推定された確率
y <- exp(b0 + b1*x)/(1+exp(b0 + b1*x))

#満足と答える確率の予測曲線（実践）
plot(
    x, y, type="l",
    xlim=c(0, 60), ylim=c(0,1),
    xlab="リハビリ単位数", ylab="満足と回答する確率"
)

#図を重ねる
par(new=T) 

#満足と答えた確率の実測値（ドット）
plot(
    満足/患者数~単位数, 
    xlim=c(0, 60), ylim=c(0,1),
    xlab="", ylab="",
    data=dat
)

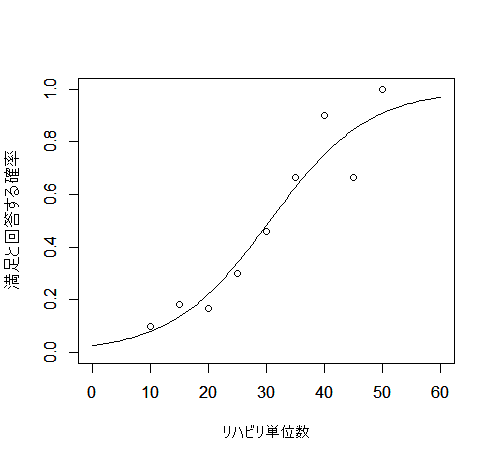
注意）ドットは実測値から求めた確率、実線は予測確率

結果の解釈

再掲

1週間のリハビリ単位数が5単位上がると、満足と回答する割合のオッズが$e^{0.1185}\fallingdotseq1.13$倍になることを意味しています

この結果の解釈はモデルから証明できます

$logit(P|x_i) =log(\dfrac{P_{x_i}}{1-P_{x_i}})=\beta_0 + \beta_1x_i$

$logit(P|x_i+1) =log(\dfrac{P_{x_i+1}}{1-P_{x_i+1}})=\beta_0 + \beta_1(x_i+1)$

$logit(P|x_i+1)-logit(P|x_i) = log(\dfrac{\dfrac{P_{x_i+1}}{1-P_{x_i+1}}}{\dfrac{P_{x_i}}{1-P_{x_i}}}) =\beta_1$

以下のようにも書けます

$\dfrac{\dfrac{P_{x_i+1}}{1-P_{x_i+1}}}{\dfrac{P_{x_i}}{1-P_{x_i}}}=\dfrac{e^{\beta_0 + \beta_1x_i}}{e^{\beta_0 + \beta_1(x_i+1)}}=e^{\beta_1}$

したがって、$ｘ_i$ が1増加するとオッズ（$\dfrac{P_{x_i}}{1-P_{x_i}}$） が $e^{\beta_1}$ 倍になることが理解できます

十分理解したうえで、結果を考察するようにしましょう！