ロジスティック回帰 (1)

パラメタ推定（対数尤度による最尤推定法）

$b_0$ と $b_1$ をどのようにして推定したのか？

最尤推定法とは、確率分布を前提にして尤度関数と最尤推定量を求める方法のことです。なんだか難しそうですが、尤度、尤度関数、最尤推定量などを例題に沿って説明してみます。

$ P_i=\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}} $   $(i=1,2,\dotsc,9)$

$P_i$ には $\beta_0$ と $\beta_1$ が含まれているので、ここでは推定するパラメタを $P$ として進めます

$ x_i=$単位数に$(i=1,2,\dotsc,9)$を当てはめることで、9つの $P_i$ を仮定します

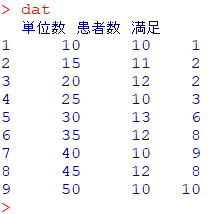
例) $i=2$の場合   $P_2=\dfrac{e^{\beta_0+\beta_1*15}}{1 + e^{\beta_0+\beta_1*15}}$

$\beta_0, \beta_1$ は未定のまま、パラメタ $P_i $ を仮定して確率分布関数（二項分布）に挿入して尤度を求めます

尤度 $= _{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i}$

このように現象からパラメタを “仮定” して求めた確率を尤度といいます

この尤度が最大になるときは尤も最もらしいパラメタ推定が行われた・・・ということで、このとき推定されたパラメタを最尤推定量といいます（最終的に算出されたパラメタ推定値を最尤推定値といいます）

例題では9つデータ（単位数 $x_i : 10, 15, …, 50$）からなり、以下の尤度関数から尤度を求めることができます

$L_{\theta}=P_1*P_2* \dotsi *P_9$  

尤度関数はパラメタ $P_i$ の関数となります（つまり尤度関数は $\beta_0,$ と $\beta_1$ の関数になります）

尤度関数

満足の確率 $P_i=\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}}$

満足ではない確率 $1-P_i=1-\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}}$

尤度関数 $L_{\theta}$

$L_{\theta}=\prod_{i=1}^{n}(\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}})^{y_i}*(1-\dfrac{e^{\beta_0+\beta_1x_i}}{1 + e^{\beta_0+\beta_1x_i}})^{n_i-y_i}$  ($n=9, n_i=$患者数, $y_i =$ 満足)

二項分布ですので以下のように書き換えることができます

$L_{\theta}=\prod_{i=1}^{n} (_{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i})$

パラメタである$P_i (\beta_0, \beta_1)$を求めるのですが、掛け算なので効率的ではありません。通常は以下のように対数変換して「足し算」に変換して求めます。

対数尤度関数

尤度$L_{\theta}$ の対数を $l_{\theta}$ （対数尤度）とします

$l_{\theta}=log(\prod_{i=1}^{n} (_{n_i}C_{y_i}P_i^{y_i}(1-P_i)^{n_i-y_i}))$

これを解くと以下のようになります ($_{n_i}C_{y_i}$ の部分は $Const$)

$l_{\theta}=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))+Const.$

この対数尤度が最大になるような$\beta_0$ と $\beta_1$ を推定します（対数尤度による最尤推定法）

$\beta_0$ と $\beta_1$ で偏微分した連立方程式を解きます

この方程式を解くためには、ニュートン-ラフソン法（Newton-Raphson法）などを用います

対数尤度はモデルのあてはまりの良さ（尤もらしさ）を示す指標となります。

Wald検定

最尤推定法より求めたパラメタの推定値$b_i$（$b_0, b_1$）が、パラメタの真の値($B_0$とする) と同じかどうかの検定

帰無仮説：$B_0=b_i$（通常は$B_0=0$を仮定する）

対立仮説：$B_0 \neq b_i$（通常は$B_0=0$を仮定する）

再掲(fit)

Estimate：最尤推定法より求めたパラメタ推定値 $b_0, b_1$（この推定値を検定します）

Std.Error：標準誤差

z value：Z検定量（推定値÷標準誤差）

Rのロジスティック回帰の係数の検定では、二項分布に基づき正規分布による検定（詳細は二項分布のページをご参照ください）でP値を求めています

Wald検定：z valueを二乗した値（Wald統計量, Wald–squareと呼ばれる）が自由度1のカイ二乗分布に従うことを利用した検定

Wald統計量$=(\dfrac{b_i-\beta_p}{SE})^2$

正規分布による検定と同じp値になるので、Rが算出しているようなZ値をWald統計量と書いていることもあるようです。下記に示す通りp値は同じ値になります。

例）単位数の係数の推定値$b_1$の検定

est <- summary(fit)$coef[2,1] 
se <- summary(fit)$coef[2,2]

#正規分布による検定
pnorm(est / se, lower.tail=F)*2

#カイ二乗分布による検定
pchisq((est / se)^2, 1, lower.tail=F)

*よく使う関数をご参照ください