確率変数と確率分布
リハビリテーションの研究になぜ確率変数が必要か?
これはリハビリテーションのデータに限らず全般的に言えることなのですが、データには誤差がつきものだからです
どんなに精巧に作られたコインでも、表の出る確率にはある程度の誤差が発生します
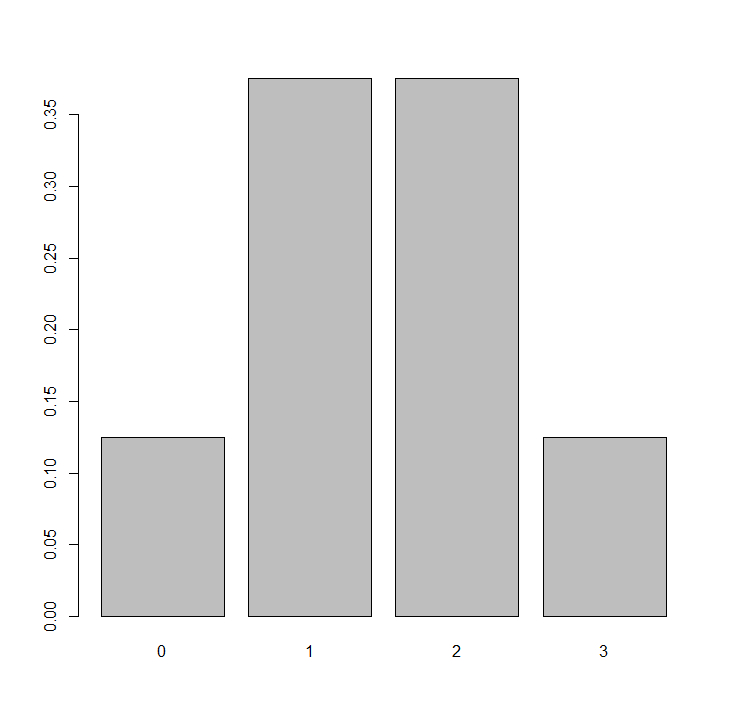
これはコインを3回投げた場合に、表が出る回数をx軸、その確率をy軸にとったグラフです
このように、結果には必ず誤差が発生します
この誤差を定式化するために確率変数という概念を利用します
上のグラフは、X軸の0, 1, 2, 3にはそれぞれの「確率」が付与されていることを意味しています
このような0, 1, 2, 3のような変数を確立変数、y軸の確率との対応関係を確立分布と言います
離散型確率分布
二項分布
確率\(π\)で2種類の結果(0または1)の値をとる独立した\(n\)回の試行の結果、1となる回数を\(k\)とすると、確率変数\(X\)は2項分布に従う
確率関数 \(P(X=k)=C^n_iπ^k(1-π)^{n-k}\)
期待値 \(nπ\)
分散 \(nπ(1-π)\)
コイン投げ(上述した例です)、表の出る確率確率\(π=\frac{1}{2}\)で3回コイン投げを実施してみた場合・・・表が出る回数\(k\)は0回、1回、2回、3回の4種類
表が出る回数\(k\)の確率変数を\(X\)とした場合、xの確率は2項分布\(B(3 , 0.5)\)に従うという

これをグラフにすると以下のようになります
t <- 0:3
p <- dbinom(x = t, size = 3, prob = 0.5)
barplot(p ~ t, pch = 16, xlab = "", ylab = "")

ベルヌーイ分布
確率\(π\)で2種類の結果(0または1)の値をとる独立した\(1\)回の試行で得られる結果の分布をベルヌーイ分布という
期待値 \(π\)
分散 \(π(1-π)\)
もちろん二項分布の\(n=1\)と同じ結果なので、\(B(1,π)\)と表される場合もあります
ポアソン分布
確率が小さく(\(π=0.02\))で2種類の結果(0または1)の値をとる独立した試行回数が多い場合(\(500\)回)、1が得られる結果を考えてみましょう
\(P(X=k)=C^{500}_{k}0.02^k(1-0.02)^{500-k}\)
この計算は現実的ではない・・・
t <- 0:20
p <- dbinom(x = t, size = 500, prob = 0.02)
barplot(p ~ t, pch = 16, xlab = "", ylab = "")
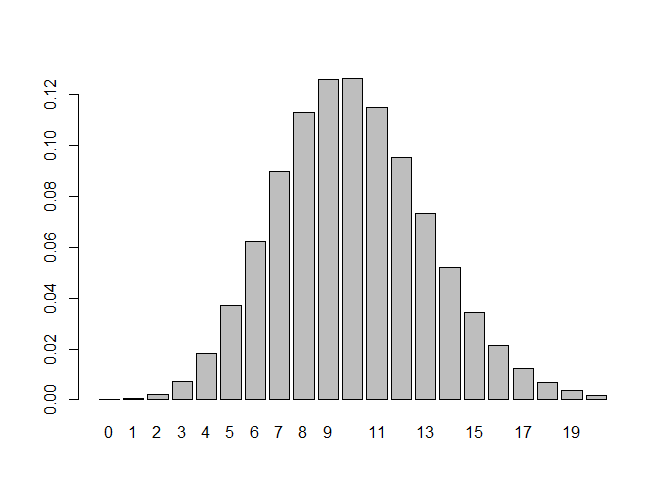
π=0.02なので500回試行して10回程度の1が得られる確率が最も多いようです
このように試行回数が非常に多く、かつ確率が非常に小さい場合には、以下の法則が成立します
ポアソンの極限定理
\(np=λ\)を固定した状態で\(n→∞\)にすることで(必然的に\(π→0\)となる)ポアソン分布が導出される
つまりポアソン分布は二項分布の極限である
\(\displaystyle \lim_{n \to \infty} C^n_kπ^k(1-π)^{n-k} = \frac{e^{-λ}λ^{k}}{k!}\)
確率関数 \(\frac{e^{-λ}λ^{k}}{k!}\)
期待値 \(λ\)
分散 \(λ\)
ポアソン分布は、\(π→0\)なので二項分布とは異なり稀に起きる現象です
ポアソン分布は、単位時間内にある事象が起きる回数の分布でパラメータはλのみです
例) \(np→10\)(固定)、\(n→∞、π→0\)の場合
t <- 0:20
p <- dpois(x = t, lambda = 10) #bが入るので注意(英語の勉強です)
barplot(p ~ t, pch = 16, xlab = "", ylab = "")
このような分布になります
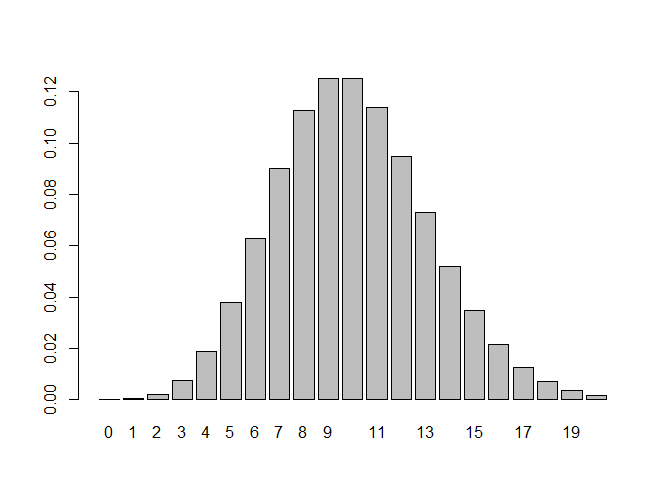
これは二項分布の成功回数20回までのグラフとほぼ同じです
t <- 0:20
p <- dbinom(x = t, size = 500, prob = 0.02)
barplot(p ~ t, pch = 16, xlab = "", ylab = "")
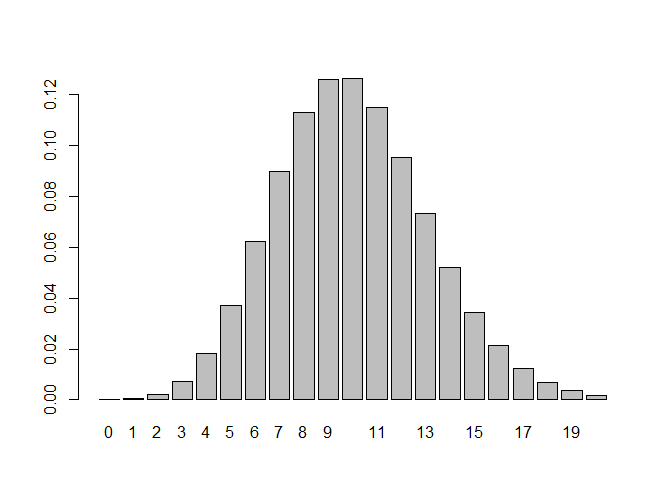
よって\(n\)が大きく\(π\)が小さい二項分布の近似として利用できます

