回帰分析 (VIF)

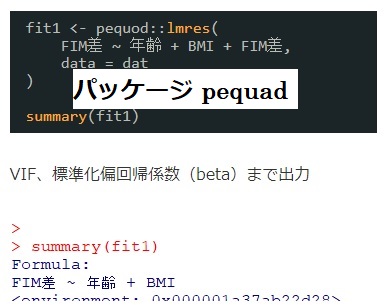
使用するパッケージ（パッケージのインストール）

library(car)

library(car)

データセット reha_data をdataに格納します（ファイルの読み込み）

データの確認

head(data)

head(data)

  age sex preFIM duration postFIM gain
1  70   0     49       10      46   -3
2  27   0     45       11      47    2
3  73   0     47       17      49    2
4  68   1     45       16      49    4
5  51   0     49       16      50    1
6  35   0     49       11      51    2

目的変数：gain ＝ postFIM – preFIM

説明変数：age, sex, preFIM, duration, postFIM

通常の回帰分析を実行します

library(car)
fit <- lm(
  gain ~ age + sex + preFIM + duration,
  data = data)
summary(fit)

library(car)
fit <- lm(
  gain ~ age + sex + preFIM + duration,
  data = data)
summary(fit)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  9.51883    3.68518   2.583   0.0105 *  
age         -0.17948    0.04070  -4.410 1.71e-05 ***
sex          6.42875    1.31565   4.886 2.14e-06 ***
preFIM      -0.09049    0.03914  -2.312   0.0218 *  
duration     0.75631    0.04302  17.580  < 2e-16 ***

次にvif関数を使用します

vif(fit)

vif(fit)

     age      sex   preFIM duration 
1.020089 1.004078 1.014628 1.002260 

VIF（Variance Inflation Factor：分散膨張係数）は、多重共線性によって回帰係数の推定が不安定になる度合いを評価する指標です。

$VIF=\dfrac{1}{1-R^2}$

$R^2$​は説明変数x1を他の説明変数x2, x3, …で回帰したときの決定係数です。つまり、$R^2$​が高い（例：説明変数x1が他の説明変数x2, x3, …と強く相関している）ほど、分母が小さくなり、VIFが大きくなります。

VIFだけで判断するのは危険です。
VIFは多重共線性の一側面しか見ていません。モデルの解釈や予測性能を総合的に判断するには、他の指標（相関係数、係数の安定性、標準誤差など）も見る必要があります。相関係数が高い変数が複数あると、モデル内での影響が重なり、係数の符号が逆転したり、有意性が変化したりすることがあります。これは「解釈の難しさ」につながります。このような場合には、変数選択や合成変数などが必要になります。