クロスオーバー試験（混合効果モデル）

反復測定分散分析：repeated measures ANOVA （混合効果モデル）
- 他のモデルと比較
事後検定

反復測定分散分析：repeated measures ANOVA （混合効果モデル）

参考文献（折笠 2016）の図10の結果。
ランダム切片モデル（各 ID ごとのランダム切片を線形回帰に取り入れたモデル）。これにより、ベースラインにおける個々の被験者の違い（ランダム効果）を調整しつつ、固定効果である sequence, treatment, period の影響を適切に分析できます。

fit3 <- lmer(
    point ~ sequence + treatment + period + (1|ID), 
    data = data
)
anova(fit3)

他のモデルと比較

分散分析表 (Between Subject) の平方和。Between SubjectですのでIDを説明変数とした線形回帰モデル。ID を固定効果として扱うことで、各被験者ごとの違いをモデルに組み込む。ただし、被験者ごとの変動を推定するのではなく、ダミー変数として扱うため、データ数が増えるとパラメータ数も増え、モデルが過学習しやすくなる。

fit4 <- lm(
    point ~ sequence + ID,
    data = data
)
anova(fit4)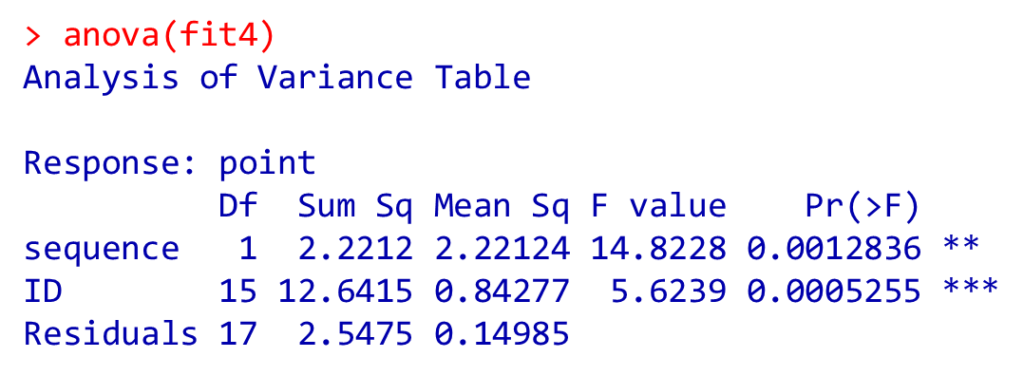

分散分析表 (Within-subject) の平方和。Within-subjectですのでIDを変量効果とした混合効果モデル。ベースラインにおける個々の被験者の違い（ランダム効果）を調整しつつ、treatment と period の影響を評価する。

fit5 <- lmer(
    point ~ treatment + period + (1|ID),
    data = data
)
anova(fit5)

比較

anova(fit3, fit4)

fit3 の方が明らかに良い（p < 0.001）。 ID はランダム効果で扱うべき。

anova(fit3, fit5)

anova(fit3, fit5) では sequence の影響が弱め（p = 0.097）だが、完全に無視できるとは言えない。

事後検定

参考文献（折笠 2016）の図11の結果。分散分析を適用します。

$\blacklozenge$ 効果の検定

fit6 <- lm(
    point ~ period + treatment + ID,
    data = data
)
anova(fit6)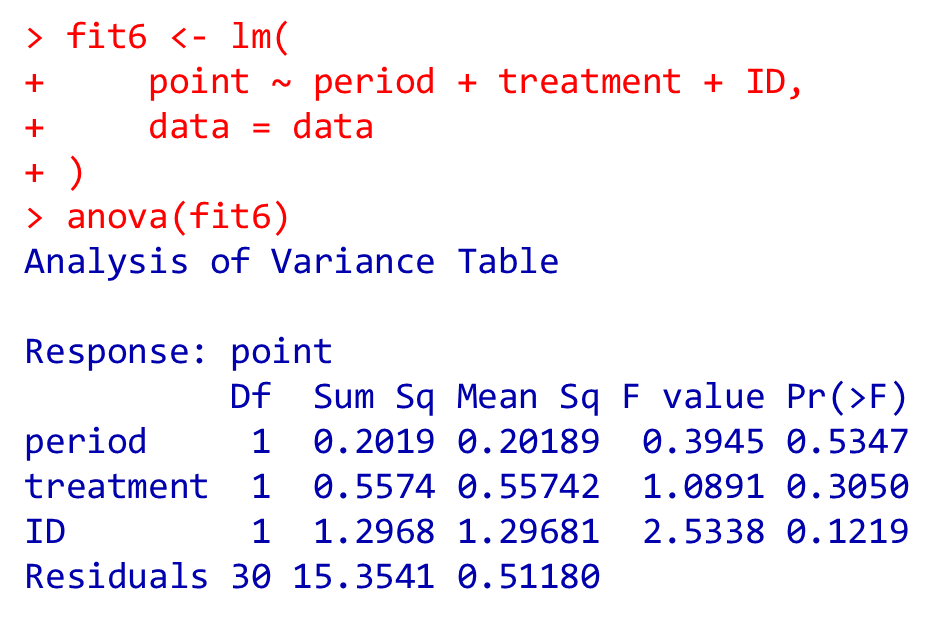

periodの結果が参考文献（折笠 2016）の図11の結果と異なります。原因が分かり次第修正します。

最小二乗平均

lmerTestのls_means関数を使用

ls_means(fit5)

$\blacklozenge$ I期、II期、治療A、治療Bの平均

mean(data[data$period=="I", "point"])
mean(data[data$period=="II", "point"])
mean(data[data$treatment=="A", "point"])
mean(data[data$treatment=="B", "point"])

最小二乗平均差

lmerTestのdifflsmeans関数。参考文献に基準を合わせます。

data$period <- relevel(data$period, "I")
data$treatment <- relevel(data$treatment, "A")
levels(data$period)
levels(data$treatment)

fit5_2 <- lmer(
    point ~ treatment + period + (1|ID),
    data = data
)

difflsmeans(fit5_2)

求め方・・・

$\blacklozenge$ 各群の最小二乗法推定量

繰り返しありと仮定して二元配置分散分析から求めます

data$period <- relevel(data$period, "II")
data$treatment <- relevel(data$treatment, "B")
levels(data$period)
levels(data$treatment)

fit7 <- lm(
    point ~ period + treatment,
    data=data
)
summary(fit7)$coef

Y11（IのA）：1.9611029 + 0.1390278 – 0.2565278 = 1.843603
Y12（IIのB）：1.9611029
Y21（IのB）：1.9611029 + 0.1390278 = 2.100131
Y22（IIのA）：1.9611029 – 0.2565278 = 1.704575
I期：(1.8436029+2.100131)/2=1.971867
II期：(1.961103+1.704575)/2=1.832839
治療A：(1.8436029+1.704575)/2=1.774089
治療B：(1.961103+2.100131)/2=2.030617

差の平均の最小二乗法推定量

I期－II期：0.1390278
治療A－治療B：－0.2565278

差の平均の最小二乗法推定量の95%信頼区間

confint ( fit7 , level = 0.95 )

参考文献
折笠秀樹. クロスオーバー試験の計画および解析. 薬理と治療, 2016, 44.9: 1261-1276.
角間辰之, 服部聡; 臨床試験のデザインと解析: 薬剤開発のためのバイオ統計. 近代科学社. 2012