経時データの解析（反復測定分散分析）

ランダム効果と固定効果
データの準備と要約

ランダム効果と固定効果

通常の線形回帰モデル

通常の線形回帰モデルは、目的変数 $y_i$を説明変数 $x_i$ と誤差項 $e_i$ を用いて説明します。モデルは次のように表されます。

$y_i = \beta_0 + \beta_1x_i + e_i$

ここで、$\beta_0$ は切片、$\beta_1$ は傾き（$x_i$ の効果）を表し、これらは固定効果です。誤差項 $e_i$ は、通常、平均 0 と一定の分散を持つ正規分布に従うと仮定されます。このモデルでは、$\beta_0$ と $\beta_1$ の固定効果をデータから推定します。

線形混合効果モデル

このモデルでは、切片と傾きにランダム効果（変量効果）を加えることで、データ内のグループ間の変動を考慮します。モデルは次のように拡張されます：

$y_i = (\beta_0+\alpha_0) + (\beta_1+\alpha_1)x_i + e_i$

$y_i = \beta_0+\beta_1x_i+(\alpha_0+\alpha_1x_i)+e_i$

ここで、$\alpha_0$ はランダム切片、$\alpha_1$ はランダム傾きを表し、これらはそれぞれのグループや個体が持つ固有の変動を捉えるためのものです。$\alpha_0+\alpha_1x_i$ はランダム効果（変量効果）であり、これらも通常、正規分布に従うと仮定されます。

線形混合効果モデルでは、固定効果 $(\beta_0、\beta_1)$ とランダム効果 $(\alpha_0, \alpha_1)$ の両方を同時に推定します。こうして、データ内の固定された傾向とランダムな変動の両方をモデル化できます。そのため、これを「混合効果」と呼びます。

データの準備と要約

例題）20名の脳卒中患者に理学療法を6週間実施して、実施前（ベースライン）、3週後、6週後の各時点でのFIM得点に差があるかどうか、有意水準は5%で検証せよ。

僕が作った架空のデータで練習しましょう。例題の内容や結果については色々とご意見があると思いますが、統計学の練習のためのサンプルですのでご了承ください。この例題は反復測定の解析になります。各観測時点のデータが独立していないので〇元配置分散分析で解析するのは間違いです。

データセット glmm をdatに格納します（ファイルの読み込み）

glmm ダウンロード

dat <- read.csv("glmm.csv", header=T, fileEncoding = "UTF-8")

$\blacksquare$ stage：ブルンストロームステージ
$\blacksquare$ period: 観測時点（bl=ベースライン、w3=3週後、w6=6週後）
$\blacksquare$ fim: FIM運動項目の得点

View(dat)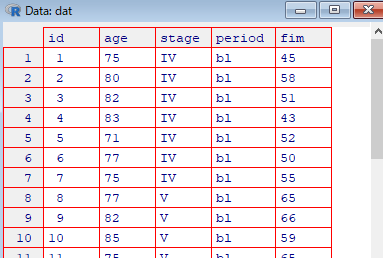

datの要約

summary(dat)

stageとperiodはただの名義変数なので基準カテゴリーがありません。欠損値が3つあります（NA’s=3）。

> summary(dat)
       id             age           stage              period               fim       
 Min.   : 1.00   Min.   :69.00   Length:60          Length:60          Min.   :43.00  
 1st Qu.: 5.75   1st Qu.:75.00   Class :character   Class :character   1st Qu.:55.00  
 Median :10.50   Median :77.00   Mode  :character   Mode  :character   Median :62.00  
 Mean   :10.50   Mean   :78.05                                         Mean   :61.39  
 3rd Qu.:15.25   3rd Qu.:82.00                                         3rd Qu.:66.00  
 Max.   :20.00   Max.   :85.00                                         Max.   :80.00  
                                                                       NA's   :3

使用するパッケージ（パッケージのインストール）

# Mixed-effects model packages
library(lmerTest)
library(nlme)
# Mixed-effects model multiple comparisons
library(multcomp)
# Using tidyr and ggplot2
library(tidyverse)
# Package for multiple comparisons
library(multcomp)

変数の変更と基準の設定

基準カテゴリー

factor() 関数は名義変数をカテゴリカル変数（因子型変数）に変換し、データのカテゴリーは「水準」として定義されます。levels() 関数で表示されるカテゴリカル変数の水準のうち、最初に表示されるカテゴリーがデフォルトで基準カテゴリー（参照カテゴリー）となり、統計モデルでの比較の基点として機能します。relevel() 関数や factor() 関数の levels 引数を使用することで、レベルの順序を指定し、基準カテゴリーを変更することが可能です。

# Convert id, period, and stage to factors
dat$id <- factor(dat$id)
dat$period <- factor(dat$period)
dat$stage <- factor(dat$stage)

基準カテゴリーを変更します。

# Set the reference level for period to 'bl'
dat$period <- relevel(dat$period, ref="bl") 
levels(dat$period)
# Set the reference level for stage to 'IV'
dat$stage <- relevel(dat$stage, ref="IV") 
levels(dat$stage)

先頭のカテゴリーが基準カテゴリーになります。

> # Set the reference level for period to 'bl'
> dat$period <- relevel(dat$period, ref="bl") 
> levels(dat$period)
[1] "bl" "w3" "w6"
> # Set the reference level for stage to 'IV'
> dat$stage <- relevel(dat$stage, ref="IV") 
> levels(dat$stage)
[1] "IV" "V"  "VI"

データの要約（縦のデータセット）

head(dat)
summary(dat)
dim(dat)

> head(dat)
  id age stage period fim
1  1  75    IV     bl  45
2  2  80    IV     bl  58
3  3  82    IV     bl  51
4  4  83    IV     bl  43
5  5  71    IV     bl  52
6  6  77    IV     bl  50
> summary(dat)
       id          age        stage   period       fim       
 1      : 3   Min.   :69.00   IV:21   bl:20   Min.   :43.00  
 2      : 3   1st Qu.:75.00   V :24   w3:20   1st Qu.:55.00  
 3      : 3   Median :77.00   VI:15   w6:20   Median :62.00  
 4      : 3   Mean   :78.05                   Mean   :61.39  
 5      : 3   3rd Qu.:82.00                   3rd Qu.:66.00  
 6      : 3   Max.   :85.00                   Max.   :80.00  
 (Other):42                                   NA's   :3      
> dim(dat)
[1] 60  5

横データの作成

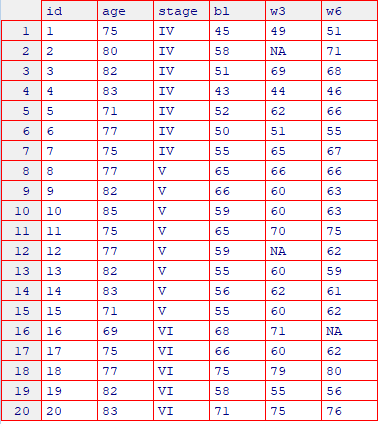
yoko <- tidyr::spread(dat, key=period, value=fim)
View(yoko)

id2 の w3, id12のw3，id16のw6に欠損が確認できます。

グラフでデータを確認

欠損値を除外したグラフ。ggplot2を使用してグラフを描く場合、欠損値（NA）は自動的に除外されます。ただし警告メッセージが表示されます。

# Basic graph settings
g1 <- ggplot2::ggplot(dat, aes(x = period, y = fim)) +
        scale_x_discrete(
            "Observation Points", 
            labels = c(
                "bl" = "Baseline", 
                "w3" = "3 Weeks Later",
                "w6" = "6 Weeks Later"
            )
        )

# Adding jitter with increased width and alpha for clarity
g2 <- g1 +
        geom_jitter(width = 0.2, height = 0, size = 2, alpha = 0.6) +  # Adjust width and alpha here
        theme(
            axis.title.x = element_text(size = 12),
            axis.title.y = element_text(size = 12),
            axis.text.x = element_text(size = 12),
            axis.text.y = element_text(size = 12)
        )

# Output the graph
print(g2)

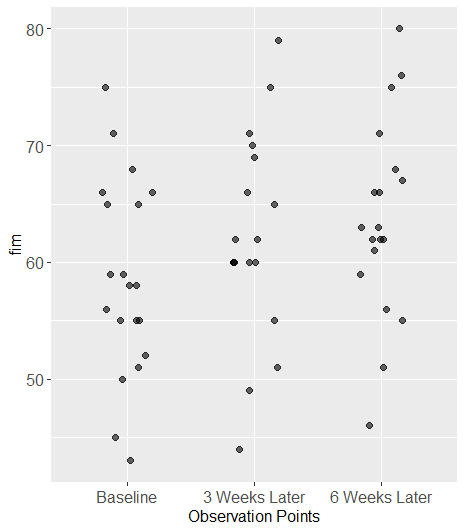
ネストしているデータ構造（マルチレベル）

上のグラフに stage と id の情報を追加します。

g3 <- g1 + 
    geom_jitter(height = 0, width = 0.1, size = 3, aes(colour = stage)) +
    geom_text(mapping = aes(label = id), vjust = 1.5) 

print(g3)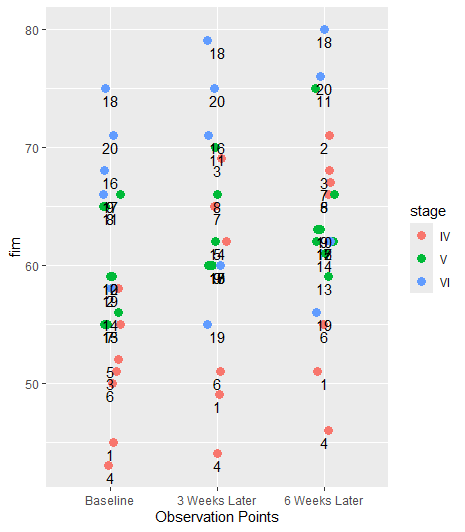

見づらい図ですが、おおよそこのようなイメージです（ageは記載してません）。これが「ネストしている」と言われるデータの構造です。図中の数字はidです（各観測時点で対応していることが理解できます）。

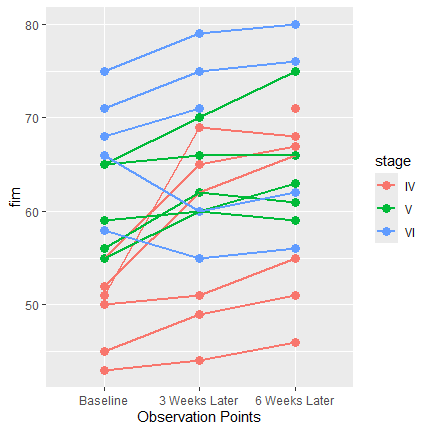
つぎに各stageごとに色分けして各時点を線で結びます。ただしデータを重ねて、IDは省略します。

# Basic graph settings and coloring by stage
g3 <- g1 + 
  geom_jitter(aes(colour = stage), height = 0, width = 0, size = 3) +
  geom_text(mapping = aes(label = ""), vjust = 1.5)
# Add lines matching the color of the stage
g4 <- g3 + 
  geom_line(aes(group = id, colour = stage), linewidth = 1)
print(g4)