主成分軸の作図(第一主成分と第二主成分)
相関係数に基づくPCA
相関行列に基づいて実行された主成分分析(PCA)の結果を用いて、第一主成分(PC1)をx軸に、第二主成分(PC2)をy軸にした散布図を作成します.ここでは、元のデータを標準化してからPCAが適用されています.標準化されたデータに対するPCAは、変数間の相関に基づいています.結果として得られる主成分スコアは、新しい座標系(主成分の軸)に沿って配置されたデータポイントを示します.
# 主成分スコアをデータフレームに変換
pca_scores <- data.frame(pca_result$x)
# ggplotで散布図を描画し、0のラインを強調
ggplot(pca_scores, aes(x = PC1, y = PC2)) +
geom_point() +
geom_text(aes(label = seq_along(PC1)), vjust = 1.5, color = "red") +
geom_hline(yintercept = 0, color = "red", size = 0.7) +
geom_vline(xintercept = 0, color = "blue", size = 0.7) +
labs(title = "相関行列に基づくPCA",
x = "第一主成分",
y = "第二主成分") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5)) # タイトルを中央揃え
*エラーが表示される場合がありますが、グラフには問題ありません
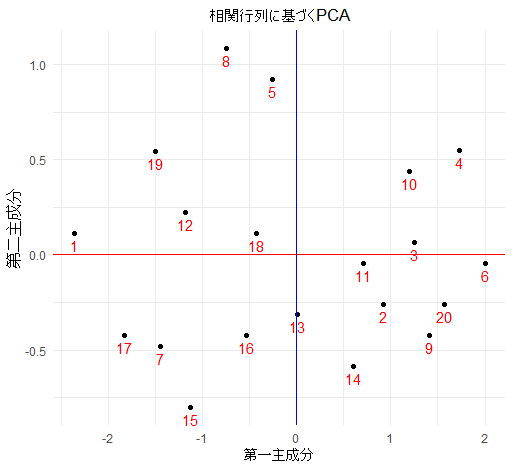

元のデータと比較したら位置が反転してしまうので、図を調整します.図の解釈が直感的になり、元のデータの特徴やパターンと一致する形で視覚化できます.PCAの結果はデータの分散が要になるので、グラフを反転しても問題はありません.
pca_result$x[, 1] <- -pca_result$x[, 1] #第一主成分を反転
pca_result$x[, 2] <- -pca_result$x[, 2] #第二主成分を反転
pca_result_2 <- pca_result
pca_scores <- data.frame(pca_result_2$x)
# ggplotで散布図を描画し、0のラインを強調
ggplot(pca_scores, aes(x = PC1, y = PC2)) +
geom_point() +
geom_text(aes(label = seq_along(PC1)), vjust = 1.5, color = "red") +
geom_hline(yintercept = 0, color = "red", size = 0.7) +
geom_vline(xintercept = 0, color = "blue", size = 0.7) +
labs(title = "相関行列に基づくPCA",
x = "第一主成分",
y = "第二主成分") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))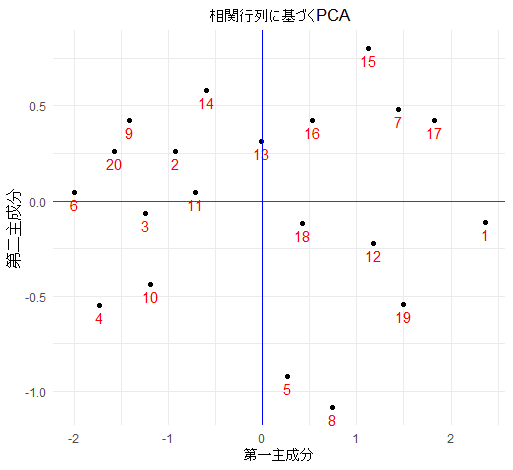
PCAの固有ベクトル(主成分の軸)は正または負の方向が反転していても、データの分析には影響しません.これは、固有ベクトルの方向が反転しても、それに対応する固有値(分散の大きさ)に変化がないためです.そのため、グラフの軸を反転させても、データの解釈における数学的な意味は変わらないという点が重要です.
バイプロット

練習なので2変数のみで進めます!
バイプロットは、主成分スコアと負荷量を示すことで、PCAの結果を視覚化します.つまり、変数が主成分に与える影響の強さと方向を同時に示します.この図では、プロットで主成分スコアを表し、矢印で各変数の負荷量を表します.バイプロットは、変数間の関係やデータセット全体の主要な動向を示します.
主成分スコア:バイプロットでは、通常、第一主成分をx軸、第二主成分をy軸にして、主成分スコアをプロットします.データ間の相対的な位置関係やクラスタリングの傾向が視覚的に捉えられます.
負荷量:各変数の負荷量は、主成分軸に対する寄与の度合いと方向を示すために矢印で表されます.矢印の始点は原点に設定され、方向と長さはその変数がデータの分散にどれだけ貢献しているかを示します.矢印が長いほど、その変数は主成分の形成に大きく寄与しており(その変数がデータ全体の分散の大部分を占めている)、矢印の方向はその変数がデータセット内でどのようなパターンを示しているかを反映します.
biplot(pca_result_2, expand = 1, arrow.len = 0.1)expand の使用は、特にバイプロットにおいて変数の寄与を理解する上で非常に便利ですが、それは軸自体のスケールを変更するわけではなく、変数ベクトルの表示方法を調整するものです.したがって、これは主に視覚的な効果のための調整であり、分析の本質的な解釈を変えるものではありません.
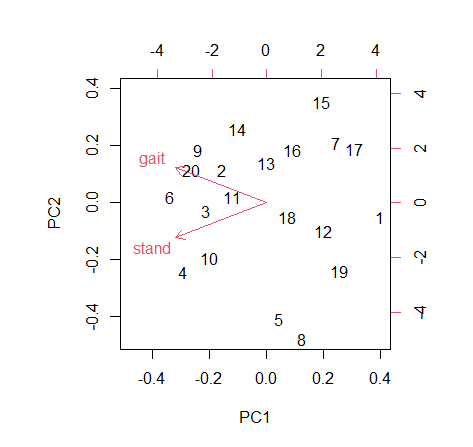
矢印の長さ
矢印の長さは、その変数が元データ(data)の分散をどれだけを説明しているかを示します. gaitとstandの矢印の長さが同じであれば、「元データの分散に対して同等の重要性を持つ」と解釈できます.つまり、gaitとstandはPC1とPC2に対して同等の影響を持っていることを意味します.
矢印の方向
正の相関関係:矢印が同じ方向を向いている場合、それらの変数は正の相関関係にあります。これは、一方の変数が増加するともう一方の変数も増加する傾向があることを示します。バイプロット上で、このような矢印は互いに並行またはほぼ同じ方向に位置します。gaitとstandは、同じ傾向にはあるようですが、それほど強い相関関係にはないようです.
負の相関関係:矢印が正反対の方向を向いている場合、それらの変数間には負の相関関係が存在します。つまり、一方の変数が増加するともう一方の変数は減少する傾向があります。これらの矢印はバイプロット上で180度の角度を形成します。
無相関関係:矢印が直角に交差している場合(つまり、互いに垂直である場合)、それらの変数間には相関がないことを示します。これは、一方の変数の変動がもう一方の変数の変動と独立していることを意味します。バイプロット上でこれらの矢印は90度の角度を形成します。

結果は同じなのですが、矢印を向きを変えたい場合は以下のようなコードになります
# 主成分スコアとローディングの符号を反転
pca_result$x[, 1] <- -pca_result$x[, 1] # 第一主成分のスコアの符号を反転
pca_result_2$rotation[, 1] <- -pca_result_2$rotation[, 1]
pca_result_3 <- pca_result_2
# バイプロットで結果を確認
biplot(pca_result_3, expand = 0.8, arrow.len = 0.1)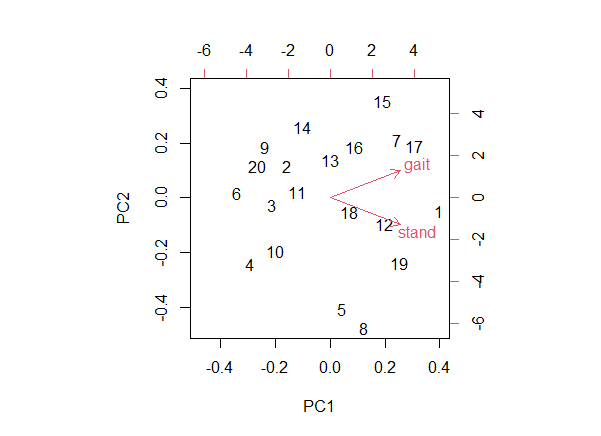
符号反転によって点(サンプル)と矢印(ローディング)が左右反転しますが、点と矢印の相対的な位置関係は保持されます。

バイプロットの解釈を行う際は、変数ベクトルの相対的な長さと位置を常に意識することが重要です.これにより、各変数が主成分にどの程度影響を与えているか、またそれらがどのように相互作用しているかを正確に把握することが可能となります.

これまでは理解のために2変数で解析してきましたが、PCAは多変量になったときに威力を発揮します.サンプルデータ(dat)を全て使用して、factoextraパッケージでバイプロットをサクッと描いてみましょう.
library(factoextra)
# PCAの計算
pca2_result <- prcomp(dat[,2:5], scale = TRUE)
# fviz_pca_biplotの結果をbiplotオブジェクトに保存
biplot <- fviz_pca_biplot(pca2_result,
geom_ind = "point", # 個体の表示方法
geom_var = "arrow", # 変数の表示方法
col.ind = "black", # 個体の色
col.var = "red", # 変数の色
labelsize = 5, # ラベルのサイズ
repel = TRUE # ラベルが重ならないように調整
)
# x軸とy軸のラベルを設定してプロット
biplot +
labs(
x = paste0("PC1 (", round(pca2_result$sdev[1]^2 / sum(pca2_result$sdev^2) * 100, 1), "%)"),
y = paste0("PC2 (", round(pca2_result$sdev[2]^2 / sum(pca2_result$sdev^2) * 100, 1), "%)")
)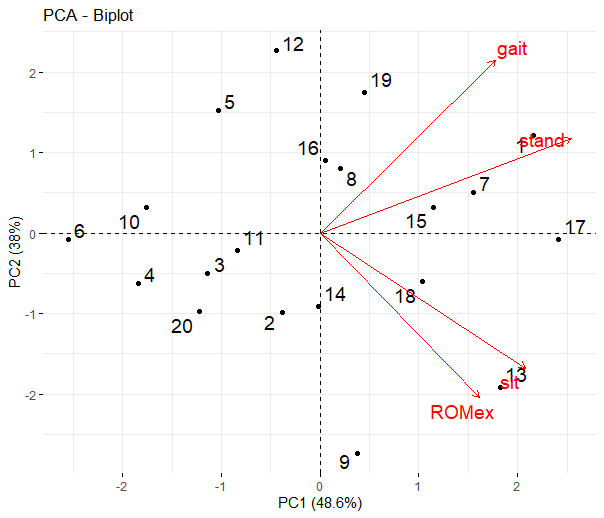
4変数のデータを第一主成分と第二主成分に射影した結果に基づいたグラフになります。PC1が全体の48.6%を説明しており、PC2が38%を説明しています。standの矢印の長さが、他の矢印よりやや長いことから、standの寄与が最も大きいようです。gaitとstandが似た方向を向いており、一方でsitとROMexが近い方向を向いています。これは、それぞれの変数ペアが相関関係にあり、2つのクラスターが形成されていることを示唆しています。

結果だけでよければ、ここまででOKです.ここからは軸の求め方について少し勉強してみましょう!

