主成分分析(PCA：Principal Component Analysis)

PCAの理論

PCAの理論

データの基本構造の基礎

データセット（行列）

$ \mathbf{M}=\begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{bmatrix} $

各列のベクトル（転置で表示）・・・これが各変数になります

$\begin{align*} \boldsymbol{x}_1^T &= \begin{bmatrix} x_{11} & x_{21} & \cdots & x_{n1} \end{bmatrix}, \\ \boldsymbol{x}_2^T &= \begin{bmatrix} x_{12} & x_{22} & \cdots & x_{n2} \end{bmatrix}, \\ & \vdots \\ \boldsymbol{x}_p^T &= \begin{bmatrix} x_{1p} & x_{2p} & \cdots & x_{np} \end{bmatrix} \end{align*}$

データセット（行列）の転置

$ \mathbf{M^T}=\begin{bmatrix} x_{11} & x_{21} & \cdots & x_{n1} \\ x_{12} & x_{22} & \cdots & x_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ x_{1p} & x_{2p} & \cdots & x_{np} \end{bmatrix} $

相関行列と分散共分散行列

　主成分分析（PCA）では、変数間の線形関係を捉えるために、相関行列に基づく方法と分散共分散行列に基づく方法があり、それぞれデータの特性に応じて選択されます．
　多変量データの相関構造は、相関行列（標準化データの場合）または分散共分散行列（未標準化データの場合）に含まれています．データを標準化すると、その分散共分散行列は相関行列に等しくなります．これは、相関係数が「単位に影響されない」ため、異なる単位を持つ変数間でも直接比較が可能であることを意味します．

相関行列と共分散行列の関係

　標準化されたデータを使用することで、異なる単位やスケールを持つ変数間でも公平に比較が可能となり、次元削減時に特定の変数が過度に影響を与えることを防げます．この場合、分散共分散行列の代わりに相関行列が使用され、各要素は変数間の相関係数を表します．標準化により各変数の分散が1になるため、相関行列の対角要素は全て1となり、非対角要素には各変数間の相関係数が示されます．

3変数を例にした場合に、相関行列と共分散行列の間には以下のような関係式も成り立ちます．

相関行列 $R=\begin{pmatrix} 1 & \rho_{12} & \rho_{13} \\ \rho_{12} & 1 & \rho_{23} \\ \rho_{13} & \rho_{23} & 1 \end{pmatrix}$

共分散行列 $C=\begin{pmatrix} \sigma_1^2 & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_2^2 & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_3^2 \end{pmatrix}$

行列 $U$ は各変数の標準偏差の逆数を対角成分に持つ対角行列：

$U=\begin{pmatrix} \dfrac{1}{\sqrt{\sigma_1^2}} & 0 & 0 \\ 0 & \dfrac{1}{\sqrt{\sigma_2^2}} & 0 \\ 0 & 0 & \dfrac{1}{\sqrt{\sigma_3^2}} \end{pmatrix}$

相関係数 $\rho_{ab}=\dfrac{\sigma_{ab}}{\sigma_a \sigma_b}$ より、関係式 $R=UCU^T$ が成り立ちます（ただし、$U^T = U$ であるため、実質的には $R = UCU$ と同じです）。

固有値、固有ベクトル

固有ベクトルとは、正方行列（ここでは相関行列）による線形変換を受けても、方向が変わらず、スカラー倍されるだけの特殊なベクトルです．通常のベクトルは行列を掛けると向きが変わることが多いのですが、固有ベクトルは向きが変わらず、長さ（スカラー）だけが変化します．固有値は、固有ベクトルがどの程度伸び縮みするかを示す数値です．例えば、固有値 $\lambda = 2$ なら、固有ベクトルの長さは$2$倍に伸び、$\lambda = 0.5$ なら半分に縮むことを意味します．

$A$は、n次正方行列とする

$Av=\lambda v$

この式を満たすベクトル$v$（零ベクトルではない）が存在する場合、スカラ―$\lambda$を$A$の固有値と呼び、ベクトル$v$を$A$の固有ベクトルと呼ぶ．

相関行列に基づくPCAにおける主成分軸の求め方

データの標準化: 各観測値から変数の平均を引き、その変数の標準偏差で割ることで、各変数を標準化します．これにより、各変数の平均が0、標準偏差が1となり、すべての変数が同じスケールに調整され、比較可能になります．
相関行列の作成: 標準化されたデータから共分散行列を計算しますが、この場合の共分散行列は相関行列と等しくなります．これは、標準化されたデータの分散が1であるため、共分散行列の要素が変数間の相関係数になるためです．
固有値分解: 相関行列を固有値分解し、固有値と固有ベクトルを求めます．この固有ベクトル（主成分軸）はデータの最大分散方向を示し、固有値はその方向の分散の大きさを表します．大規模なデータや高次元データの場合、計算の効率化のために特異値分解が利用されることがあります．
主成分の選択: 固有値が大きい順に固有ベクトルを選び、データの重要な特性を捉える主成分を決定します．
主成分スコア: 選択した主成分軸に元のデータを射影し、新しい主成分得点（スコア）を計算します．

1. データの標準化

データセットを標準化して得られた行列を $X$ とします。標準化により、異なる単位や尺度を持つデータを統一的に扱うことが可能となり、主成分分析（PCA）の結果が各変数のスケールに依存しないものになります．

2. 相関行列の作成

標準化されたデータ行列 $X$ から相関行列 $R$ を求めます．

$R = \frac{1}{n-1} X^T X$

$X^T$: $X$ の転置行列
$n$: サンプルサイズ

相関行列は変数間の線形関係の強さを示します．標準化されていない元のデータを用いると共分散行列になります．

サンプルデータdatの2～5列目を使用して、相関行列 $R$ を算出してみます

data <- dat[, 2:5]
x <- scale(data)
n <- nrow(data)
R <- t(x) %*% x / (n-1)
print(R)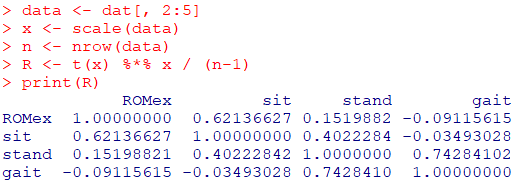

関数corで確認してみます

cor(data)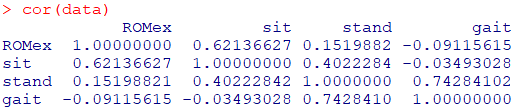

3. 固有値分解

相関行列 $R$ に固有値分解を適用し、$v$（固有ベクトル）と$\lambda$（固有値）を求めます．

$R v=\lambda v$

相関行列 $R$ は半正定値対称行列であるため、以下の性質を持ちます：

全ての固有値 $\lambda$ は非負です．
固有ベクトルは互いに正規直交します．

なぜ固有値分解が必要なのか？
主成分の軸の方向：固有ベクトル$v$は、データセットの分散が最大となる新しい軸を示します．固有ベクトル$v$により、多次元データセットにおけるデータの主要な変動方向やパターンを捉えることができます．
各軸の分散：固有値$λ$ は、それぞれの固有ベクトルが示す方向におけるデータの分散の大きさを表します．固有値が大きいほど、その方向におけるデータの分散も大きいということになります．

固有値と固有ベクトルを求めるRコード

#固有値
lambda <- pca_result$sdev^2
print(lambda)
#固有ベクトル
vectors <- pca_result$rotation
print(vectors)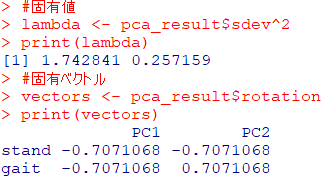

寄与率

第一主成分の寄与率＝$\dfrac{第一主成分の固有値}{第一主成分の固有値+第二主成分の固有値}$

lambda[1]/{lambda[1]+lambda[2]}

4. 主成分の選択

　固有値の中で最も大きいもの（最大固有値）に対応する固有ベクトルが、第一主成分の軸を示します．このベクトルの方向が、データの分散が最大になる方向を表します．主成分分析では、この方向がデータの最も重要な構造を捉えていると考えます．累積寄与率が一定の割合（例えば85%）に達するまでの主成分を選択することが一般的です．

5. 主成分スコア

　固有値分解により得た固有ベクトル（主成分の軸）に基づいて、各データ点の新しい軸上での位置（主成分スコア）を求めることができます．実際の算出方法は、標準化されたデータの行列に、各主成分の固有ベクトルを掛けることになります．この操作により、元の多次元データを主成分と呼ばれる新しい低次元の特徴空間に投影することが可能になります．このスコアは、データを低次元で効果的に要約するものであり、パターン認識やデータのさらなる分析に有用です．

$z_k = X v_k$

$z_k: $ 第$k$主成分の主成分スコア
$X$: 標準化されたデータ行列
$v_k$: 第$k$主成分の固有ベクトル

主成分分析における最適化の理論的アプローチ

　ラグランジュの未定乗数法は、制約付き最適化問題を解くための効果的な数学的ツールです．PCAにおけるこの方法の使用は、主成分が分散を最大にする方向（データセット全体の分散を最大化する主成分軸）を求めるという特定の目的に対して用いられます．ラグランジュの未定乗数法の詳細は記事下のチャンネルをご覧ください．

相関行列 $R$: 標準化された変数の共分散行列であり、データの主要な構造を反映します．この行列の固有ベクトルはデータの分散を最大化する方向、すなわち主成分軸を表します．
$R$の固有ベクトル $v$: 射影分散$v^T R v$を最大にする方向を示し、それぞれの固有値 $\lambda $はこの方向の分散の大きさを定量化します．
ラグランジュ関数 $L(v, \lambda) $: $v^T R v$を最大化することを目的とし、ノルムが 1 $( v^T v = 1 )$という制約のもとで設定されます。偏微分を行い、固有値問題 $ Rv = \lambda v $ へと導きます。

射影分散

射影分散$v^T R v$ は、ある方向ベクトル$v$ にデータを射影したときの分散を計算します．この値が大きいほど、その方向に沿ってデータは広がりを持っており、データセットの変動がよく表現されていることになります．したがって、この射影分散を最大にする方向ベクトル$v$が、データの主要な構造、すなわちデータのばらつきが最も大きい方向を示しています．具体的には、最初の主成分はデータ全体の分散を最も大きく説明する方向を捉え、次の主成分はその次に分散を最大にする方向（既に見つけた主成分と直交する）を示します．これにより、元のデータセットの情報を最大限に保持しつつ、次元を削減することが可能になります．これは、特にデータの可視化やノイズの多いデータからの重要な情報の抽出に有効です．この過程を通じて、データの主要な構造を数学的に厳密に捉えることができ、それに基づいてデータ解析や予測モデルの構築が行えます．

ラグランジュ関数の設定
　主成分分析（PCA）における主成分軸を求める問題は、射影分散 $v^T R v$ を最大化することとして定式化されます．ただしノルムが1という制約$(v^T v = 1)$のもとで行います．この制約付き最適化問題を解くため、ラグランジュ関数を設定します．

$L(v, \lambda) = v^T R v – \lambda (v^T v – 1)$

ラグランジュ関数の偏微分
最適解を得るため、ラグランジュ関数を $v$ に関して偏微分し、その結果をゼロと設定します：

$\frac{\partial L}{\partial v} = 2R v – 2\lambda v = 0$

これは、固有値問題 $Rv = \lambda v $ を示しており、固有値分解によって解を求めることができます．

まとめ
主成分分析（PCA）の主な目的は、データの分散を最大化する方向（主成分軸）を見つけ、データの次元（今回の例では理学療法の4項目）を効果的に縮約することです．この解析は理論的には制約付き最適化問題として扱われます．その解法の一つとして、ラグランジュの未定乗数法が理論的枠組みとして用いられます．具体的には、標準化された変数の相関行列 $R$ に対する固有値問題 $Rv = \lambda v$ を解くことで、分散を最大化する方向（固有ベクトル＝主成分軸）と、その方向に沿った分散の大きさ（固有値）が求められます．実際のPCAでは、固有値分解や特異値分解（SVD）が主に利用され、これらの手法を用いることで効率的に計算が行われます．これにより、データの主要な変動方向を効果的に抽出し、次元削減やデータ解析のための基盤を提供します．

ラグランジュの未定乗数法については、以下をご覧ください