平均、分散、不偏分散

1ページ　2ページ　3ページ

統計量（z値とt値）

標本ｘが正規分布$N( \mu , \ \sigma^2 )$に従う場合

$Zvalue = \dfrac{標本平均\ – \ 母平均}{\sqrt{母分散}}= \dfrac{\overline{x}\ – \ \mu}{\sigma}$

しかし推定の場合には母分散は未知の場合が多い．そこで，標本平均の$\sqrt{標本不偏分散}$を使用してt値を求めます (不偏標準偏差と呼ばれることもある)．

$Tvalue = \dfrac{標本平均\ -\ 母平均}{\sqrt{標本不偏分散}}=\dfrac{\overline{x}\ – \ \mu}{s}$

これは正規分布には従わず、自由度 $n-1$ の t分布 に従います

付録

chat GPTの答え

分散の演算の重要な性質

$V($ 定数 $) = 0$
$V( X +$ 定数$ ) = V(X)$
$V( X + Y ) = V(X)+V(Y)$
$V( cX ) = c^2*V(X)$

証明

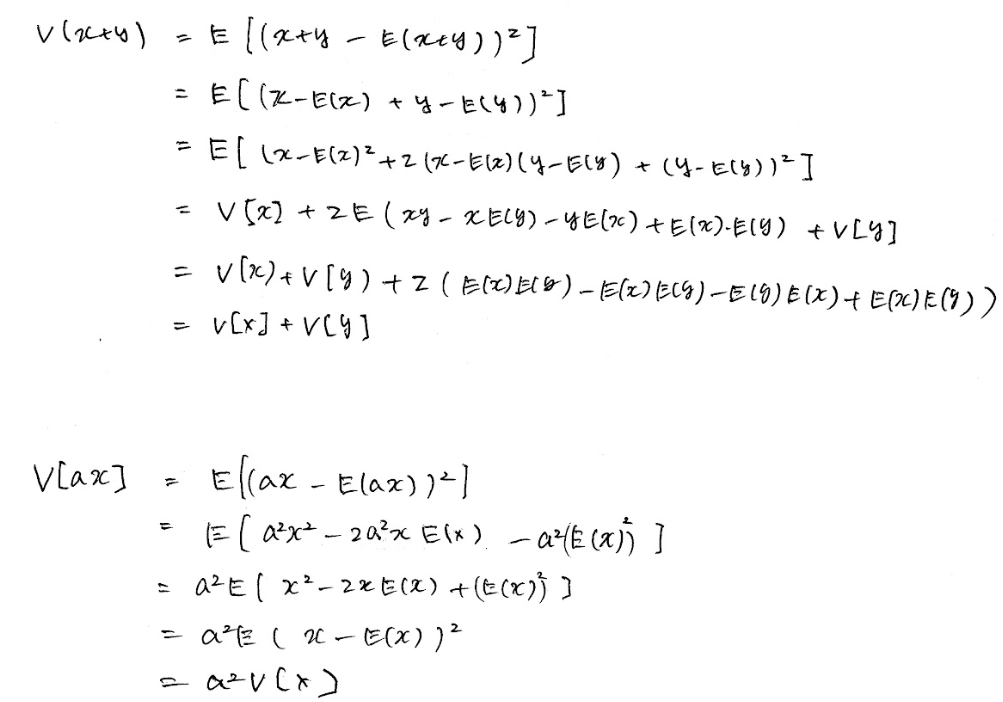
なぜ不偏分散はn-1で割るのか？

　標本分散（サンプルの分散）は、分母にサンプルサイズ n を使用するため、分散の推定値は実際の分散よりも少し小さくなります。

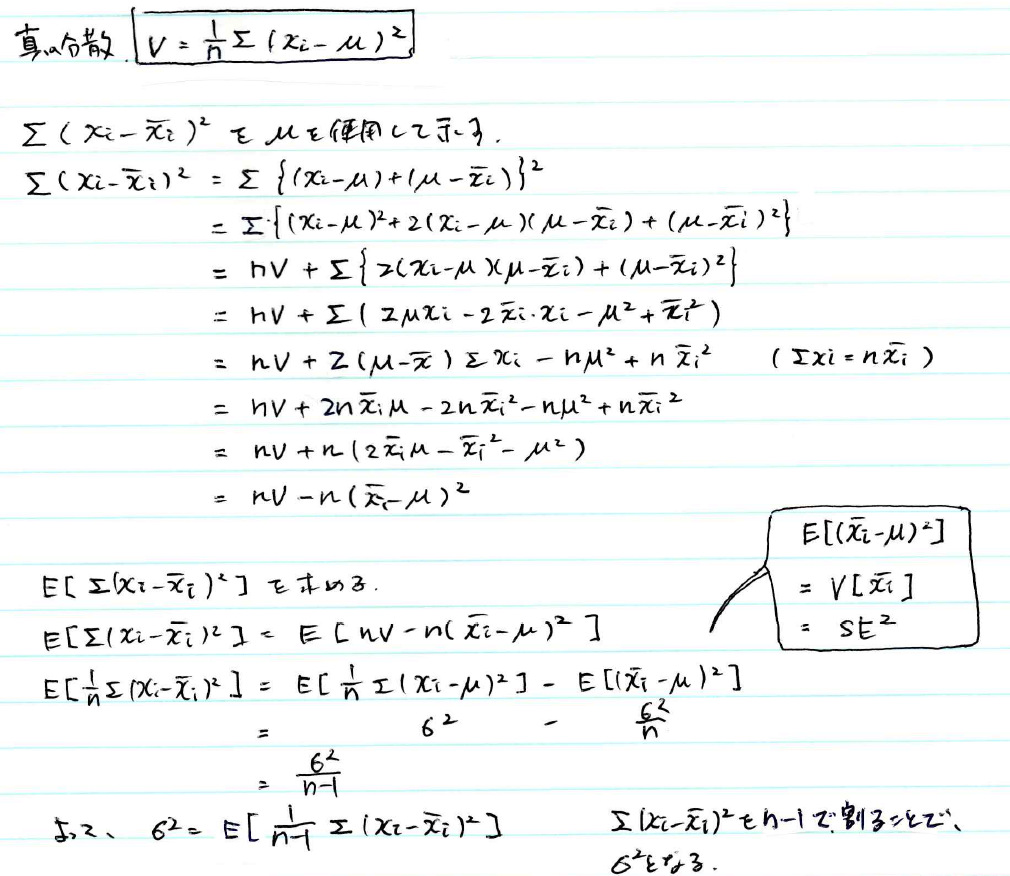
標本分散の期待値は、真の分散から$\frac{\sigma^2}{n}$の分だけ過少評価することが分かりました。このバイアスは、サンプルサイズが小さいときに顕著に表れます。これは、標本平均が偏差を完全に反映できないこと原因です。標本平均は、母平均とは異なるため、偏差が実際よりも小さく見積もられることがあります。

$E[\frac{1}{n}\sum(x_i-\overline{x_i})^2]=\sigma^2-\frac{\sigma^2}{n}$

このバイアスを修正するために、分母に n-1 を用いる不偏分散を計算します。こうすることで、自由度を考慮し、分散の不偏推定値を得ることができます。この n-1 は「自由度」として知られており、標本平均の計算に1つのパラメータ（自由度）が使用されることを補正しています。したがって、正確な分散の推定や統計的検定を行うためには、不偏分散の使用が推奨されます。特に標本サイズが小さい場合には、この補正が非常に重要になります。

$\sigma^2=E[\frac{1}{n-1}\sum(x_i-\overline{x_i})^2]$

参考
西内啓、統計学が最強の学問である［実践編］データ分析のための思想と方法　数学的補足p6-12