RとChatGPTを使った統計学の学習方法

RとChatGPTを使った統計学の学習方法

リハビリテーションに関わる煩雑な業務に携わる皆様でも、コツコツ学習できる統計学の勉強方法について記載しておきます。

準備するものは、パソコンとインターネット回線です

95%信頼区間

Rのコードであれば、ChatGPTに尋ねたら何でも教えてくれます。ただし、微妙な違いを生成AIはキャッチするので、質問内容（プロンプト）はいろいろ試してみてください。

プロンプトの例
Rを使用して次のデータの95％信頼区間を算出するコードを教えてください
10, 9, 15, 13, 12.5, 15.3, 13, 15, 21, 17.2

Rを使用して指定されたデータセットの95%信頼区間を算出するには、まずデータセットをRのベクトルとして作成し、その後mean()関数で平均値を計算し、sd()関数で標準偏差を求めます。次に、信頼区間を求めるために標準誤差を計算し、t分布を使用して信頼区間の範囲を算出します。

以下に具体的なコードを示します：

RCopy

# データセットを作成
data <- c(10, 9, 15, 13, 12.5, 15.3, 13, 15, 21, 17.2)

# 平均値と標準偏差を計算
mean_val <- mean(data)
sd_val <- sd(data)

# サンプルサイズ
n <- length(data)

# 標準誤差を計算
se <- sd_val / sqrt(n)

# 自由度
df <- n - 1

# t分布から95%信頼区間のt値を求める
t_value <- qt(0.975, df)

# 信頼区間の計算
ci_lower <- mean_val - t_value * se
ci_upper <- mean_val + t_value * se

# 信頼区間の表示
cat("95% Confidence Interval: [", ci_lower, ", ", ci_upper, "]", "\n")

このコードは、与えられたデータセットに対して95%の信頼区間を算出します。ここで、qt(0.975, df)関数は、自由度dfのt分布における上側2.5%点（つまり95%信頼区間の上限）のt値を返します。また、信頼区間の下限と上限は、平均値から標準誤差の95%信頼区間の範囲を考慮した値として計算されます。

ChatGPT

教えていただいたコードをRにペーストするだけで答えが出ます

プロンプトの例
関数を使用して簡単にできますか？

はい、Rには統計解析を行うための便利な関数が多数用意されており、これらを使うとより簡単に95%信頼区間を計算することができます。特にmean()関数とt.test()関数を組み合わせると、データセットの平均値の95%信頼区間を直接算出できます。

以下に、そのためのコードを示します：

RCopy

# データセットを作成
data <- c(10, 9, 15, 13, 12.5, 15.3, 13, 15, 21, 17.2)

# t.testを使用して95%信頼区間を計算
result <- t.test(data)

# 結果の表示
result

このコードは、t.test()関数を使用して指定されたデータの95%信頼区間を計算します。この関数は、データの平均値、95%信頼区間の下限と上限、t値、自由度、p値などの詳細な統計情報を含むリストを返します。

この方法は特に初心者にとっては、平均値の信頼区間を計算する際の複雑な手順を簡略化し、結果を簡単に解釈できるようにするために有効です。

ChatGPT

Rの出力でわからないことがあれば、ChatGPTにコピペして尋ねてみてください

プロンプトの例
以下のような回答になりました。
統計学は初心者です。
t = 12.867, df = 9の意味を分かりやすく教えてください。

One Sample t-test
data: data
t = 12.867, df = 9, p-value = 4.242e-07
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
11.62101 16.57899
sample estimates:
mean of x
14.1

統計学において、t値（t = 12.867）と自由度（df = 9）は、データが特定の統計的仮説をサポートするかどうかを判断するために使われます。ここでの「One Sample t-test」の結果を分かりやすく説明します。

t値（t = 12.867）

• 意味： t値は、サンプルデータがテストの仮説（ここでは「真の平均が0である」という仮説）からどれだけ離れているかを示します。数値が大きいほど、観測されたデータと仮説との間に大きな差があることを意味します。
• 解釈： ここでのt値は12.867です。これは、サンプル平均が仮定された平均（0）からかなり離れていることを示しています。つまり、データは「平均が0である」という仮説を支持しないことを強く示唆しています。

自由度（df = 9）

• 意味： 自由度は、統計分析における独立した値の数を表します。一般的には、サンプルサイズから1を引いた値です（サンプルサイズ – 1）。
• 解釈： ここでの自由度は9です。これは、サンプルサイズが10（10 – 1 = 9）であることを意味します。自由度は、t分布の形を決定し、結果の信頼性を判断するのに使われます。

その他の統計情報

• p値（p-value = 4.242e-07）： 非常に小さいp値は、テストの結果が偶然によるものではないことを示唆しています。通常、p値が0.05（または5%）より小さい場合、結果は統計的に有意であると考えられます。
• 95%信頼区間（11.62101 〜 16.57899）： この区間は、平均値の真の値がこの範囲内にあると95%確信できることを意味します。
• サンプル平均（mean of x = 14.1）： サンプルデータの平均値です。

このt検定の結果は、平均値が0ではないという強い証拠を提供しており、データが特定の効果や変化を示していることを強く支持しています。

ChatGPT

これからは生成AIを使用して学習する時代ですね！
とくにChatGPTはコーディングが得意です。
統計学備忘録も時代遅れにならぬよう生成AIと共生します！！！

ｔ検定

プロンプトの例
Rのコードを教えてください。
以下のデータを使用してベクトルにしてください。
また２群を比較するためのグラフや検定方法などを教えてください。
A=(10, 9, 15, 13, 12.5, 15.3, 13, 15, 21, 17.2)
B=(12, 11,8, 13.5, 18.5, 21.1, 10, 18, 22, 23.5)

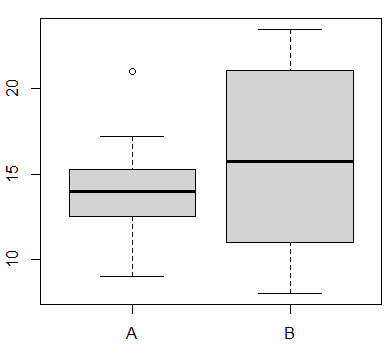
R言語を使用してデータセットAとBをベクトルとして定義し、それらを比較するためのグラフを作成し、統計的検定を行う方法を説明します。まず、ベクトルを定義し、ボックスプロットを作成してデータを視覚的に比較します。その後、t検定を使用して、2つのグループ間で統計的に有意な差があるかどうかを検証します。

RCopy

# データの定義
A <- c(10, 9, 15, 13, 12.5, 15.3, 13, 15, 21, 17.2)
B <- c(12, 11, 8, 13.5, 18.5, 21.1, 10, 18, 22, 23.5)

# ボックスプロットの作成
boxplot(A, B, names = c("A", "B"), main = "Boxplot of A and B")

# t検定の実施
t_test_result <- t.test(A, B)

# t検定の結果の出力
print(t_test_result)

このコードでは、まずベクトルAとBを作成し、boxplot関数を使用してボックスプロットを作成します。次に、t.test関数を使用して、データセットAとB間で独立した2標本t検定を実行します。最後に、t検定の結果を出力します。

このプロセスは、2つのデータセット間で平均値に統計的に有意な差があるかどうかを判断するのに役立ちます。t検定のp値が0.05未満であれば、グループ間に統計的に有意な差があると見なされます。

ChatGPT

そのままRにコピペ

プロンプトの例
以下のような出力になりました。
解析結果について、分かりやすく説明してください。

Welch Two Sample t-test
data: A and B
t = -0.80442, df = 15.125, p-value = 0.4336
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-6.055323 2.735323
sample estimates:
mean of x mean of y
14.10 15.76

この出力は、データセットAとBに対して実施されたWelchの2標本t検定の結果です。Welchのt検定は、2つの独立したサンプル間の平均値に統計的に有意な差があるかどうかを検討するために使用される検定です。この検定は、2つのサンプルの分散が等しくないという前提のもとで行われます。

結果の解釈は以下の通りです：

1. t値: -0.80442

• これは、2つのサンプル間の平均値の差を標準誤差で割った値です。t値が大きいほど、平均値の差が大きいことを示します。この場合、t値は比較的小さいです。

1. 自由度 (df): 15.125

• この値は、データセットのサイズから計算され、検定の精度を決定します。この場合、自由度は約15です。

1. p値: 0.4336

• p値は、帰無仮説（2つのサンプル間に差がない）が正しい場合に、観測された結果（またはそれ以上に極端な結果）が得られる確率です。一般に、p値が0.05未満の場合、結果は統計的に有意と見なされます。この場合、p値は0.4336であり、これは帰無仮説を棄却するには十分ではないことを意味します。つまり、AとBの平均値に統計的に有意な差はないと結論付けられます。

1. 95%信頼区間: -6.055323 から 2.735323

• これは、真の平均値の差がこの区間内にあると95%信頼できることを意味します。この区間には0（差がないことを示す値）が含まれているため、平均値に有意な差があるとは言えません。

1. サンプル推定値:

• Aの平均 (mean of x): 14.10
• Bの平均 (mean of y): 15.76
• これらはそれぞれのサンプルの平均値です。

結論として、このt検定の結果は、データセットAとBの間に統計的に有意な平均値の差がないことを示しています。

ChatGPT

グラフいろいろ

ChatGPTへ質問
RでFunnel plotを描くためのコードをサンプルも含めて教えてください

# 必要なパッケージをインストール
install.packages("metafor")
# パッケージを読み込む
library(metafor)
# 簡単な架空のデータセットを作成
dat <- data.frame(
  study = 1:10,
  effect_size = rnorm(10, 0, 1),
  se = runif(10, 0.1, 0.5)
)
# Funnel plotの描画
funnelplot <- funnel(dat$effect_size, sei = dat$se)
print(funnelplot)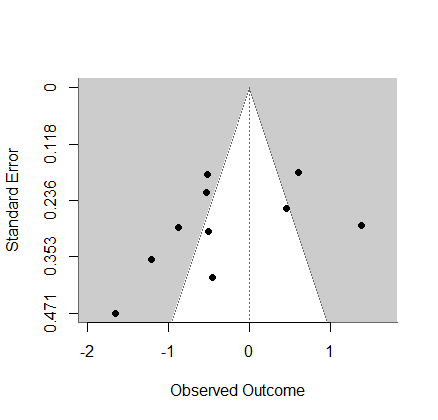

プロンプトの例
時系列のデータを２群比較したグラフ
サンプルを含めてRのコードを教えてください

# 必要なライブラリをロード
library(ggplot2)

# サンプルデータの生成
set.seed(123) # 乱数の再現性を保証
periods <- 1:10 # 時間の期間
values_before <- cumsum(runif(10, min=-2, max=2)) # 前期の値（ランダムなウォーク）
values_after <- values_before[10] + cumsum(runif(10, min=-2, max=2)) # 後期の値（前期の最終値からスタート）

# データフレームの作成
data <- data.frame(
  period = c(periods, periods), # 期間
  value = c(values_before, values_after), # 値
  phase = factor(c(rep("Before", 10), rep("After", 10))) # 前後の区分
)

# 線グラフの描画
ggplot(data, aes(x=period, y=value, group=phase, color=phase)) +
  geom_line() + # 線グラフ
  geom_point() + # データポイント
  theme_minimal() + # シンプルなテーマ
  labs(title="Before and After Comparison", x="Period", y="Value") + # タイトルと軸ラベル
  scale_color_manual(values=c("Before"="blue", "After"="red")) # 色の手動設定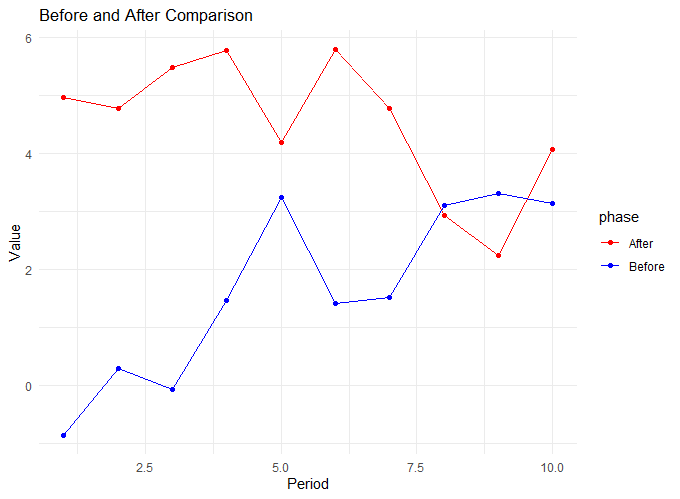

プロンプトの例
フォレストプロットの描き方
サンプルを含めてRのコードを教えてください

# パッケージのロード
library(metafor)

# サンプルデータの生成
dat <- data.frame(
  study = c("Study 1", "Study 2", "Study 3", "Study 4", "Study 5"),
  effect_size = c(0.2, 0.5, 0.3, 0.7, 0.4), # 効果量（例：log odds ratio）
  se = c(0.1, 0.15, 0.2, 0.12, 0.18) # 効果量の標準誤差
)

# メタアナリシスモデルのフィット
res <- rma(yi=effect_size, sei=se, data=dat, method="REML")

# フォレストプロットの作成
forest(res, slab=dat$study, xlab="Effect Size", alim=c(-1, 1), at=log(c(0.5, 1, 2)), atransf=exp, 
       xlim=c(-1, 2), cex=0.8, ilab=cbind(dat$effect_size, dat$se), ilab.xpos=c(-0.25, -0.5), 
       ilab.pos=2, psize=1, digits=2, mlab="Random Effects Model", addfit=TRUE)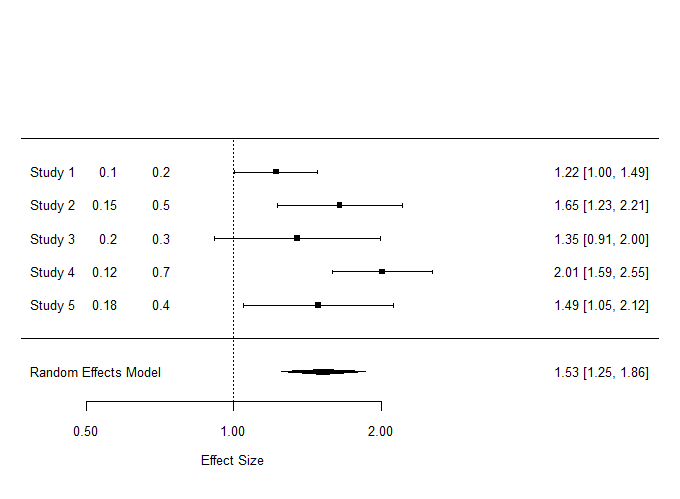

プロンプトの例
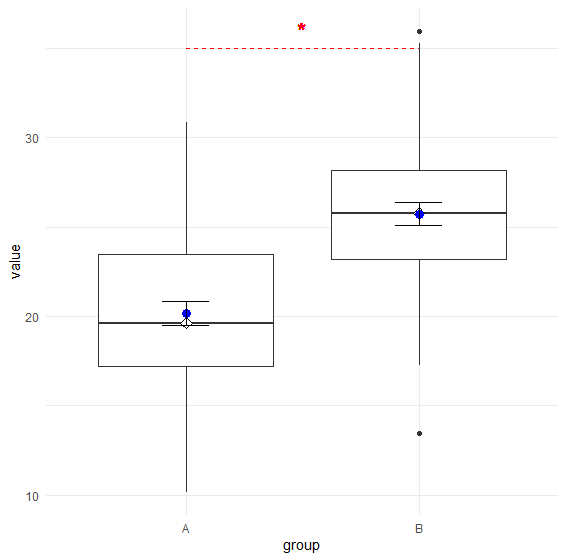
次のRのコードを教えてください
２群の比較のグラフ それぞれの平均値とSEを示して、
2群の有意差を示すアスタリスクもつけてください

# 必要なライブラリのロード
library(ggplot2)

# サンプルデータの生成
set.seed(123)  # 結果の再現性のため
group_A <- rnorm(50, mean=20, sd=5)
group_B <- rnorm(50, mean=25, sd=5)

data <- data.frame(
  value = c(group_A, group_B),
  group = factor(rep(c("A", "B"), each=50))
)
# 箱ひげ図の描画と中央値、平均値とSEの表示
p <- ggplot(data, aes(x=group, y=value)) +
  geom_boxplot() +
  stat_summary(fun=median, geom="point", shape=23, size=3, fill="white", aes(group=group)) +  # 中央値
  stat_summary(fun=mean, geom="point", color="blue", size=3, aes(group=group)) +  # 平均値
  stat_summary(fun.data=mean_se, geom="errorbar", width=0.2, aes(group=group)) +  # 平均値のSE
  theme_minimal()

# 2群間に線を引き、アスタリスクで有意差を示す
p + geom_segment(aes(x=1, y=35, xend=2, yend=35), linetype="dashed", color="red") +
  geom_text(aes(x=1.5, y=36, label="*"), color="red", size=6)