超幾何分布を使用した検定
例題:有意水準5%の片側検定の例
帰無仮説:重症群と軽症群では効果の割合に差がない
対立仮説:軽症群より重症群の方が効果ありの割合が多い(片側検定)
P(X=12)+P(X=13)+P(X=14)+P(X=15) を求めてみましょう
x <- 12:15
sum(dhyper(x, 15, 14, 18))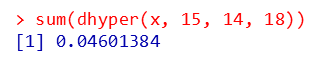
p値<0.05なので、「軽症群より重症群の方が効果ありの割合が有意に多い」という結果になります。Fisherの正確検定は超幾何分布を使っているので同じP値が算出されます。
cross3 <- matrix(c(12, 6, 3, 8), ncol = 2)#分割表の作成
print(cross3)
fisher.test(cross3, alternative = "greater")$p.value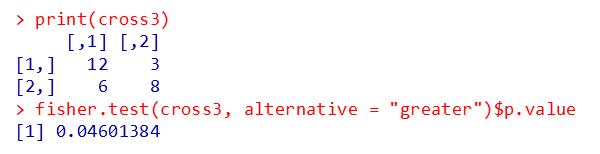
非復元抽出法(袋から取り出した玉は、袋に戻さない)

超幾何分布は、非復元抽出を前提としています。上述した治療効果の例ではイメージしずらいので赤玉と白玉を使って説明してみます!
ここまで治療Aの効果で説明してきましたが、統計学のテキストでは赤玉と白玉の例がよく紹介されています。赤玉と白玉が混在する袋から無作為に取り出したサンプルの中に含まれる赤玉の数の確率を調べる際に、超幾何分布を用いることができます。超幾何分布は、非復元抽出法で採取されたサンプルの確率分布です(1つずつ袋から取り出し、取り出した玉は袋に戻しません)。N 個の玉(赤玉:M個、白玉:N-M個)入っている袋から非復元抽出法で取り出した k 個の中に含まれる赤玉の数を x 個とします。そして、その赤玉 x の数を確率変数 X とみなした場合、X の分布は超幾何分布に従います。
cross4 <- matrix(c(
"x", "k-x", "k",
"", "", "",
"M", "N-M", "N"),
ncol = 3)
colnames(cross4) <- c("Balls out", "Balls in", "sum")
rownames(cross4) <- c("Red", "White", "sum")
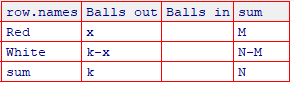
View(cross4)Balls out: the number of balls taken from the bag
Balls in: the number of balls left in the bag
Red: the number of red balls in the bag
White: the number of white balls in the bag
母集団 N のサイズが無限に大きい場合($N \rightarrow \infty$)
母集団 N のサイズが非常に大きい場合には(大きな袋がパンパンになっている状況)、超幾何分布は二項分布に近似します。一つの要素(例えば赤玉)を抽出しても母集団の構成(パンパンの袋)にほとんど影響を与えず、各抽出が独立しているとみなせるからです。つまり、非復元抽出であっても、母集団のサイズが非常に大きければ、一度抽出された要素が次の抽出に与える影響は無視できるほど小さくなります。従って、母集団のサイズ N が無限大、またはそれに近い場合、非復元抽出の超幾何分布は、各試行が独立しているとみなせる二項分布に近似できます(二項分布は、独立した試行を複数回行い、各試行で成功する確率が一定である場合の確率分布です)。
$\dfrac{M}{N}=p$(所謂、成功確率)
期待値:$E(X) = n\dfrac{M}{N} = np $
分散:$V(X) = n\dfrac{M(N-M)}{N^2}\dfrac{N-n}{N-1} = np(1-np)\dfrac{N-n}{N-1}$
N が非常に大きい場合、$\dfrac{N-n}{N-1}$は、1に収束します。従って、修正された分散式は V(X) = np(1-p)となり、二項分布の分散と一致します。
おまけ)復元抽出法

1つずつ袋から取り出し、取り出した玉は袋に戻します(復元抽出法)。復元抽出法では、袋から玉を取り出した後にそれを袋に戻すため、各抽出が独立しています。この独立性のため、超幾何分布ではなく二項分布が使用されます。
二項分布の確率質量関数 $P(X=x) = \binom{n}{x} p^x (1-p)^{n-x} $
n: 試行回数(取り出す玉の数)
x: 成功回数(例えば赤玉を取り出す回数)
p: 1回の試行で成功する確率
期待値:E(X) = np
分散:V(X) = np(1-p)
$N \rightarrow \infty$ の場合に、二項分布は中心極限定理により近似的に正規分布に従います



