指数分布を一般化したもの
確率密度関数
- \(f(x)=\frac{λ^α}{Γ(α)}x^{α-1}e^{-λx}\) \((x≧0)\)
- \(f(x)=0\) \((x<0)\)
・2つのパラメタがあります\(Ga(α, λ)\)と表します
・\(α=1\)の場合、指数関数になります
期待値:\(\frac{α}{λ}\)
分散:\(\frac{α}{λ^2}\)
・確率変数\(X\)が\(N(0,1)\)に従う場合、\(X^2\)は\(Ga(\frac{1}{2}, \frac{1}{2})\)に従う
・\(Ga(\frac{k}{2}, \frac{1}{2})\)は、自由度\(k\)のカイ二乗分布といわれる
ガンマ関数
- \(Γ(α)=\int_{0}^{∞}x^{α-1}e^{-x}dx \)
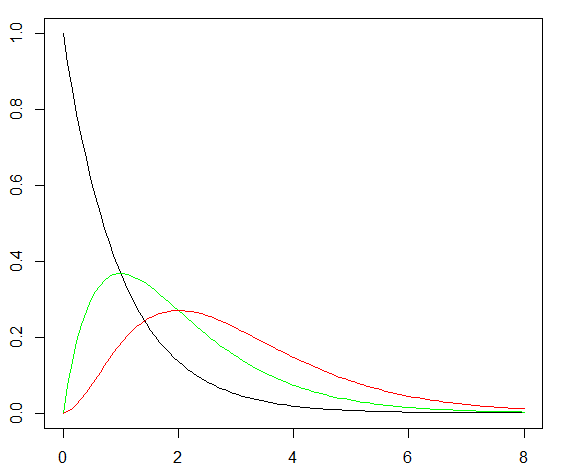
ガンマ分布のグラフ \(Ga(α, λ)\)
- \(α: shape\)
- \(\frac{1}{λ}: scale\)
\(λ = 1\)の場合、\(scale=1\)
R
curve(dgamma(x , shape = 1 , scale = 1) , 0 , 8)
curve(dgamma(x , shape = 2 , scale = 1) , 0 , 8 , add = T , col = "green")
curve(dgamma(x , shape = 3 , scale = 1) , 0 , 8 , add = T , col = "red")