中心極限定理

2022.12.30

中心極限定理とは

　無作為に抽出された独立標本の和または平均の分布は、有限の平均と分散を持つ任意の母集団分布から抽出された場合、標本サイズが増加するにつれて正規分布に近づきます。特に、標本サイズが大きくなると、標本平均の分布は母集団の平均と同じ期待値を持ち、その分散は母集団の分散を標本サイズで割ったものになります。標本平均の標準偏差は母集団の標準偏差を標本サイズの平方根で割ったものであり、これは分布の変動を測るための指標です。理論的には、標本サイズが非常に大きくなると、標本平均の分布は正規分布に収束します。
　一般的に標本サイズが30以上であれば、多くの場合において標本平均の分布は正規分布に近いと見なされますが、母集団分布が大きく歪んでいる場合や極端な値を持つ場合は、より大きな標本サイズが必要となることがあります。

平均値の収束について、少し数式を加えて解説

任意の母集団分布において、その平均を $\mu$、分散を $\sigma^2$ とします。この母集団から無作為に抽出された独立標本の平均を $\bar{X}$ とすると、標本サイズ $n$ が増加するにつれて、 $\bar{X}$ の分布は正規分布 $N(\mu, \dfrac{\sigma^2}{n})$ に近づきます。

$\bar{X} \approx N(\mu, \dfrac{\sigma^2}{n})$

ここで、標本平均の期待値は母集団の平均に等しく、分散は母集団の分散を標本サイズ $n$ で割ったものになります。標本平均の標準偏差は母集団の標準偏差 $\sigma$ を標本サイズの平方根 $\sqrt{n}$ で割ったものになります。

標本平均の標準偏差：$\dfrac{\sigma}{\sqrt{n}}$​

分布が歪んでいる場合や外れ値が多い場合は、正確な正規近似を得るためにより大きな $n$ が必要となります。理論的には、$n \rightarrow \infty $ で、$\bar{X}$ の分布は完全に正規分布 $N(\mu, \dfrac{\sigma^2}{n})$ に収束します。

正規分布
通常はNormal distributionと呼ばれているのですが、この分布はC.F.ガウス(1777-1855)の誤差関数に由来することからGaussian distributionとも呼ばれています。
y2pt.com
2023.01.03

平均0、分散1の正規分布からのサンプリング

サンプルサイズが10、20、30と増加するにつれて、サンプル平均が母平均に近づき、サンプル分散が母分散に近づく傾向が観察されます。特に、サンプル平均の分布はサンプルサイズが大きくなると正規分布に収束し、これは中心極限定理によって説明されます。

R
# 必要なパッケージをロード
library(ggplot2)

# サンプルサイズを設定
sample_sizes <- c(10, 20, 30, 100, 200, 300)

# 各サンプルサイズでのシミュレーション結果をプロット
plot_list <- list()
for (n in sample_sizes) {
  # 正規分布からn個のサンプルを抽出
  samples <- rnorm(n, mean = 0, sd = 1)
  
  # データフレームを作成
  data <- data.frame(x = samples)
  
  # ヒストグラムと正規分布曲線を重ねてプロット
  p <- ggplot(data, aes(x = x)) +
  geom_histogram(
    aes(y = ..density..), 
    binwidth = 0.5, 
    color = "black", 
    fill = "gray"
  ) +
  stat_function(
    fun = dnorm, 
    args = list(mean = 0, sd = 1), 
    color = "red", 
    size = 1
  ) +
    ggtitle(paste("Sample Size =", n)) +
    theme_minimal()
  
  plot_list[[length(plot_list) + 1]] <- p
}

# グラフを並べて表示
library(gridExtra)
do.call(grid.arrange, plot_list)

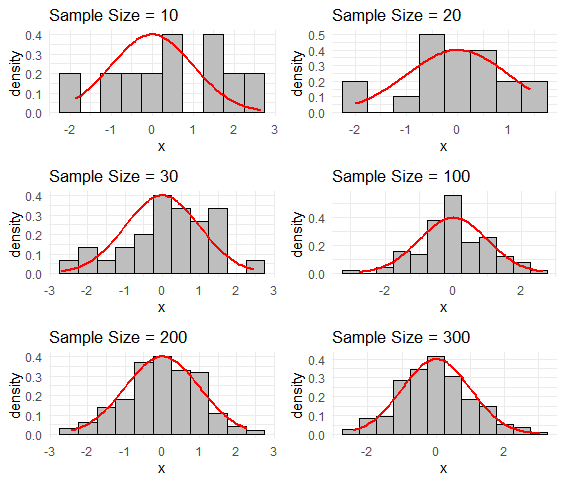
平均値の分布を確認

平均0、分散1の正規分布からのサンプリングを繰り返し実施することで、平均値の分布を知ることができます。サンプルサイズを10, 20, 30, 100, 200, 300と設定して、それぞれ1000回ずつサンプリングを繰り返します。そこで得た平均値の分布をヒストグラムで視覚的に評価します。

R
# 必要なパッケージをロード
library(ggplot2)

# サンプルサイズの設定
sample_sizes <- c(10, 20, 30, 100, 200, 300)

# 繰り返し抽出回数（1000回）を設定
iterations <- 1000

# サンプル平均を格納するためのリストを初期化
sample_means <- list()

for (n in sample_sizes) {
  means <- numeric(iterations)
  for (i in 1:iterations) {
    samples <- rnorm(n, mean = 0, sd = 1)
    means[i] <- mean(samples)
  }
  sample_means[[as.character(n)]] <- means
}

# データフレームを作成
data <- data.frame(
  sample_size = rep(sample_sizes, each = iterations),
  mean = unlist(sample_means)
)

# グラフをプロット
ggplot(data, aes(x = mean, fill = as.factor(sample_size))) +
  geom_histogram(aes(y = ..density..), binwidth = 0.1, alpha = 0.7) +
  facet_wrap(
    ~ sample_size, 
    scales = "fixed", 
    labeller = labeller(sample_size = label_both)
  ) +
  theme_minimal() +
  ggtitle("サンプルの平均値の分布") +
  xlab("サンプルの平均値") +
  ylab("密度") +
  guides(fill = guide_legend(title = "サンプルサイズ"))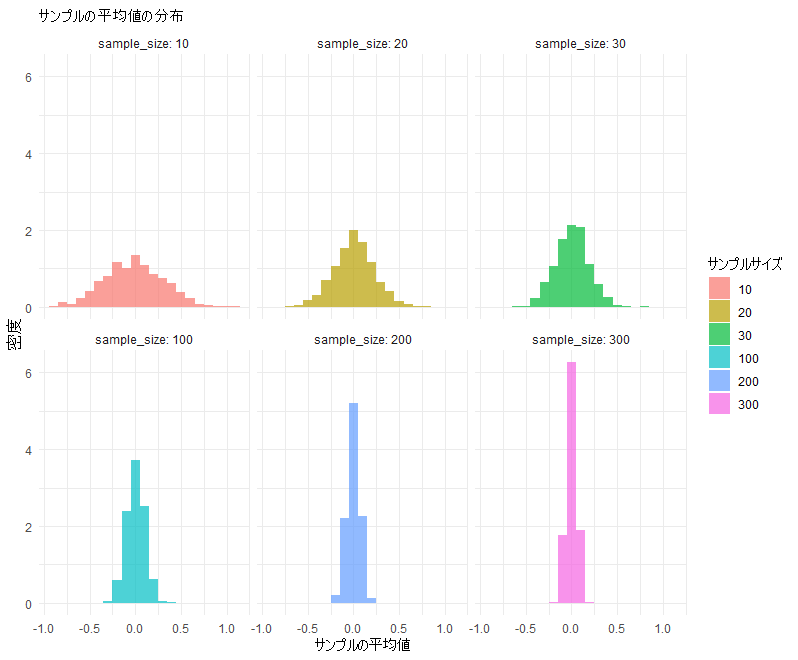

サイコロを使用した実験

　中心極限定理は、二項分布においても適用されます。例えば、サイコロを投げて1が出た場合を「成功」とします。試行回数 $n$ が大きくなるにつれて、標本の成功回数の分布は二項分布からの正規分布に近づきます。
　サイコロの1が出る確率 $\dfrac{1}{6}$ です。サイコロを振る回数 $n$ を1回, 2回, 5回, 10回, 20回, 30回と徐々にふやしていき、二項分布を利用して成功回数（1が出る回数）を求めます。

実験1) コインを １回 投げた場合、表になる確率と裏になる確率

確率 $\dfrac{1}{6}$ に従う二項分布より確率を求めます

二項分布とベルヌーイ分布
リハビリテーション統計学に必須の確率分布です。地域Aの「週に1回以上の頻度で運動する人の割合」を50％とします. この地域からお互いに全く関係のない3名（Aさん、Bさん、Cさん）をランダムに選んで実施した二者択一のアンケート結果から確率を求めてみましょう・・・？
y2pt.com
2023.01.01

確率関数 \(P(X=k)={}_n C_kπ^k(1-π)^{n-k}\) より

コインの表確率=$\dfrac{1}{6}$, 試行回数１回, 成功回数０,１回

$\pi=\dfrac{1}{6}, ｎ＝1, ｋ＝\{0、1\}$

R
#空のベクトル k() を作成・・・二項分布の成功回数に該当する
k <- c()
#成功回数0回（表が０回＝裏）、成功回数1回（表が１回）
#k <- c(0, 1)を作成
for(i in 0: 1)
k <- c(k, i) 
#コインを投げた回数（試行回数）
n <- 1  
# コインの表確率
pi <- 1/6
#裏になる確率と表になる確率
P1 <- choose(1, k)*(pi^k)*(1 - pi)^(n - k)  
print(P1)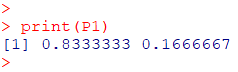
R
#表が0枚, 1枚となる確率のグラフ
barplot(P1, space=c(0.5), names.arg=c(0, 1), xlab="1が出る回数")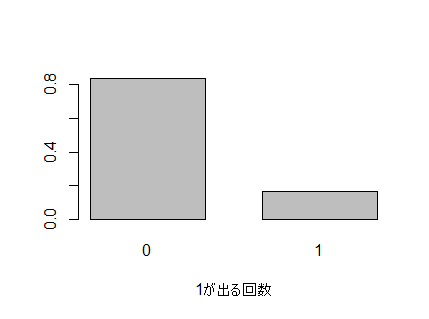
実験2) コインを ２回 投げた場合に、表が 0回, 1回, 2回 となる確率
R
#空のベクトル k() を作成・・・二項分布の成功回数に該当する
k <- c()
#成功回数0回（表が０回＝裏）、成功回数1回（表が１回）
#k <- c(0, 1)を作成
for(i in 0: 2)
k <- c(k, i) 
#コインを投げた回数（試行回数）
n <- 2 
# コインの表確率
pi <- 1/6
#裏になる確率と表になる確率
P2 <- choose(n, k)*(pi^k)*(1 - pi)^(n - k)  
print(P2)
R
barplot(P2, names.arg=c(0, 1, 2))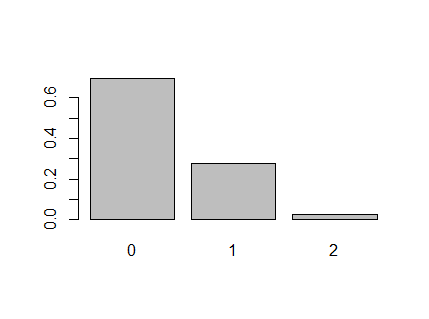

binom関数を使えばもっと簡単です

R
probabilities <- dbinom(x=k, size=n, prob=pi)
print(probabilities)
実験3) コインを 5回 投げた場合に、表が0回, 1回, …, 5回 となる確率
R
n <- 5
k <- c()
for(i in 0: n)
k <- c(k, i) 
pi <- 1/6
p5 <- dbinom(x=k, size=n, prob=pi)
barplot(p5, names.arg=c(0:n))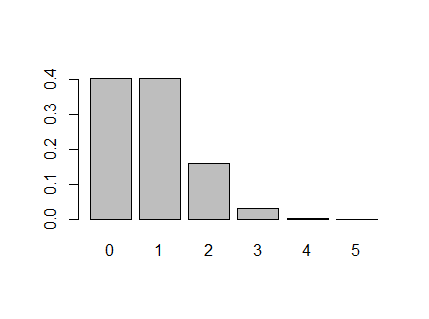
実験4) コインを 10回 投げた場合に、表が0回, 1回, …, 10回 となる確率
R
n <- 10
k <- c()
for(i in 0: n)
k <- c(k, i) 
pi <- 1/6
p10 <- dbinom(x=k, size=n, prob=pi)
barplot(p10, names.arg=c(0:n) )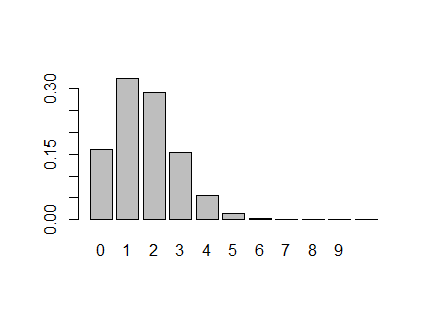
実験5) コインを 20回 投げた場合に、表が0回, 1回, …, 20回 となる確率
R
n <- 20
k <- c()
for(i in 0: 12)
k <- c(k, i) 
pi <- 1/6
p20 <- dbinom(x=k, size=n, prob=pi)
barplot(p20, names.arg=c(0: 12))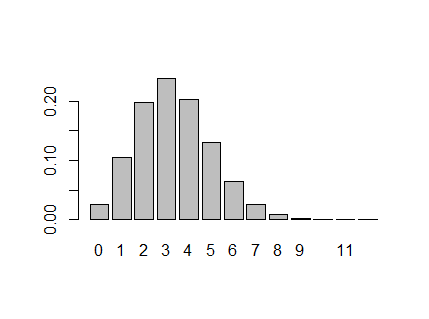
実験6) コインを30回投げた場合に、表が0回, 1回, …, 30回 となる確率
R
n <- 30
k <- c()
for(i in 0: 12)
k <- c(k, i) 
pi <- 1/6
p30 <- dbinom(x=k, size=n, prob=pi)
barplot(p30, names.arg=c(0:12), xlab="表の回数")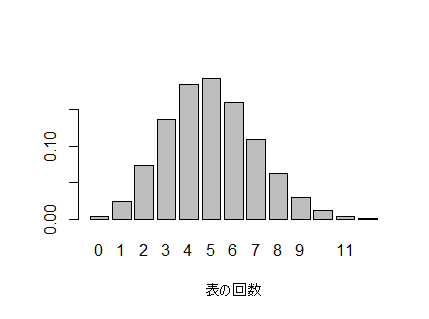

実験で描いたグラフ

R
par(mfrow = c(2,3))
  barplot(P1, space=c(0.5), names.arg=c(0, 1), xlab="1が出る回数")
  barplot(P2, names.arg=c(0, 1, 2))
  barplot(prob5, main="実験3 (5回)")
  barplot(prob10, main="実験4 (10回)")
  barplot(prob20, main="実験5 (20回)")
  barplot(prob30, main="実験6 (30回)")
par(mfrow = c(1, 1))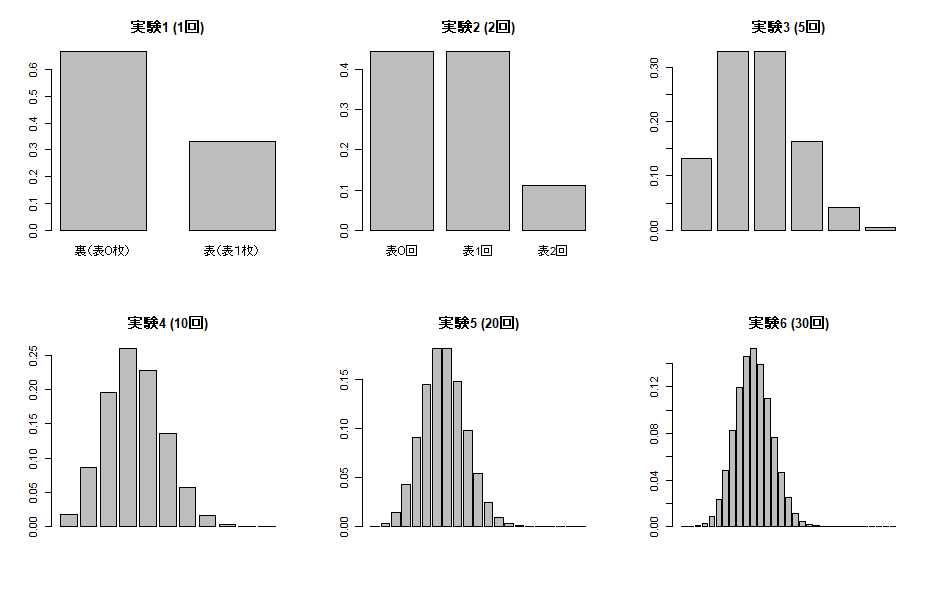

ちにみに10000回投げた場合・・・

R
a <- 1666-200
b <- 1666+200
k <- c()
for(i in a: b)
k <- c(k, i) 
n <- 10000
pi <- 1/6
prob10000 <- dbinom(x=k, size=n, prob=pi)
barplot(prob10000, names.arg=c(a: b), xlab="表の回数")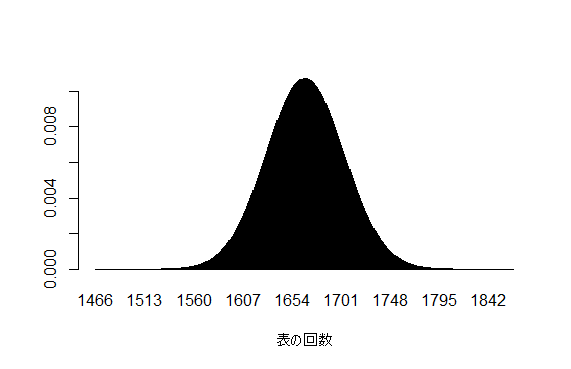

参考) 西内 啓; 統計学が最強の学問である[実践編]—データ分析のための思想と方法, ダイヤモンド社, 2014

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください

タイトルとURLをコピーしました