p値いろいろ
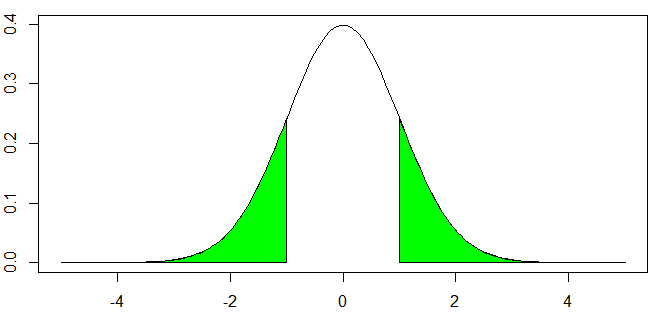
\(Z=\pm 1\)の場合:P値はおおよそ\(\dfrac{1}{3}\)
R
#グラフ
xseq <- seq(-5, 5,length=100)
plot(xseq, dnorm(xseq, 0, 1),type="l")
p <- seq(-5, -1, length=100)
y <- dnorm(p, 0, 1)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="green")
p <- seq(1, 5, length=100)
y <- dnorm(p, 0, 1)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="green")R
#両側のp値
pnorm(-1)+pnorm(1, lower.tail=F)
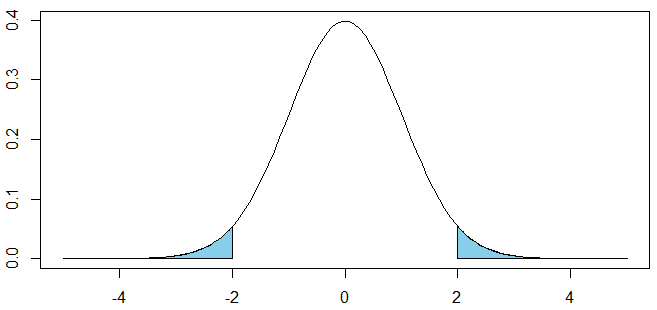
\(Z=\pm 2\)の場合:P値はおおよそ\(\dfrac{1}{20}\)
R
#グラフ
xseq <- seq(-5, 5,length=100)
plot(xseq, dnorm(xseq, 0, 1),type="l")
p <- seq(-5, -2, length=100)
y <- dnorm(p, 0, 1)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="skyblue")
p <- seq(2, 5, length=100)
y <- dnorm(p, 0, 1)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="skyblue")R
pnorm(-2)+pnorm(2, lower.tail=F)
偏差値
標準正規分布より
\(T=Z \times 10 + 50\)
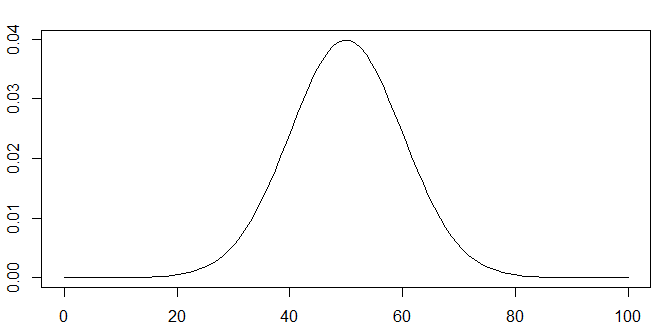
上の図の平均を50、標準偏差を10としたグラフになるので
R
#グラフ
xseq <- seq(0, 100, length=100)
plot(xseq, dnorm(xseq, 50, 10),type="l")標準正規分布と同じ考え方で、1500人のなかで偏差値70点の順位を推定してみましょう
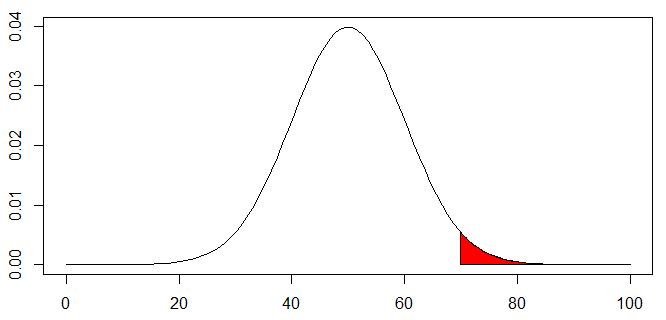
下図の確立を求めてみます
R
#グラフ
xseq <- seq(0, 100, length=100)
plot(xseq, dnorm(xseq, 50, 10),type="l")
p <- seq(70, 100, length=100)
y <- dnorm(p, 50, 10)
polygon(c(p,rev(p)), c(rep(0,length(p)), rev(y)), col="red")偏差値70以上の確立(赤塗り部分)
R
#p値
pnorm(70, 50, 10, lower.tail=F)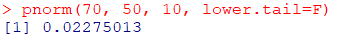
2倍したら、もちろん


標準正規分布と全く同じことを繰り返してるだけですね・・・
自分より上位には約2.27%いることがわかりましたので、おおよその順位を出してみましょう
1500×0.0227=34
1500人の試験で偏差値70の場合、だいたい30位くらいに位置していることが理解できました
参考文献
統計学入門 - 東京大学出版会
統計学入門詳細をご覧いただけます。
302 Found

