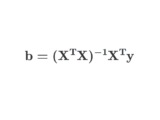単回帰分析

おまけ1：線形代数を利用した計算方法
おまけ2：係数検定のための標準誤差

おまけ1：線形代数を利用した計算方法

重回帰のときにとても便利です

表記の定義：$x_{ij}$の場合、$i$はデータセットの行、$j$はデータセットの列を示す

$y_{i}=b_0+b_1x_{ij}+\dotsc+b_jx_{ij}+\varepsilon_{i} \quad i={1,2,\dotsc,n} \quad j={1,2,\dotsc,k}$

$
\mathbf{X}=
\left(\begin{array}{ccc}
1 & x_{11} & \dotsc & x_{1k} \\
1 & x_{21} & \dotsc & x_{2k} \\
\vdots & \vdots & \ddots & \vdots \\
1 & x_{n1} & \dotsc & x_{nk}
\end{array}\right)
$

$
\mathbf{y}=
\left(\begin{array}{cc}
y_1 \\
y_2 \\
\vdots \\
y_n
\end{array}\right)
\quad$$
\mathbf{b}=
\left(\begin{array}{cc}
b_0 \\
b_1 \\
\vdots \\
b_m
\end{array}\right)
\quad$$
\mathbf{0}=
\left(\begin{array}{cc}
0 \\
0 \\
\vdots \\
0
\end{array}\right)
$

とした場合、パラメタ推定の公式は以下のようになります

$\mathbf{b}=(\mathbf{X^T}\mathbf{X})^{-1}\mathbf{X^T}\mathbf{y}$

もちろん単回帰分析でも使用可能です。今回のデータ（lm01）を当てはめて解いてみましょう。

dat$b <- c(rep(1, dim(dat)[1]))
df <- dat[ ,c("b",  "PT単位数")]
mat <- as.matrix(df)

solve(
    t(mat) %*% mat
    ) %*% 
    t(mat) %*% 
    dat$FIM差

              [,1]
b        2.8593665
PT単位数 0.4983616

Rの関数で算出した係数と同じ値になりましたね！（再掲）

fit <- lm(FIM差~PT単位数, data=dat)
print(fit)

> print(fit)

Call:
lm(formula = FIM差 ~ PT単位数, data = dat)

Coefficients:
(Intercept)     PT単位数  
     2.8594       0.4984

おまけ2：係数検定のための標準誤差

$Y = \beta_0 + \beta_1x_i + e_i$

$\beta_0$ の推定値を $b_0$ 、$\beta_1$ の推定値を $b_1$ とすると

$E[b_0]=E[\bar{y}-\bar{x}b_1]=\beta_0$

$E[b_1]=E[\dfrac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2}]=\beta_1$

$V[b_0]=\sigma^2(\dfrac{1}{n}+\dfrac{\bar{x}^2}{\sum(x_i-\bar{x})^2})$

$V[b_1]=\dfrac{\sigma^2}{\sum(x_i-\bar{x})^2}$

(再掲)

fit <- lm(FIM差~PT単位数, data=dat)
summary(fit)

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)   2.8594     2.8642   0.998   0.3514  
PT単位数      0.4984     0.1660   3.002   0.0199 *

$\sigma^2$ の推定 $s^2$

$s^2=\dfrac{\sum{(y_i-\hat{y_i})^2}}{n-2} \qquad$ 自由度=$n-$パラメタ数（単回帰の場合は2）

$\beta_0$ の検定

Std.Error = $\sqrt{V[b_0]}=\sqrt{s^2(\dfrac{1}{n}+\dfrac{\bar{x}^2}{\sum(x_i-\bar{x})^2})}$

$\beta_1$ の検定

Std.Error = $\sqrt{V[b_1]}=\sqrt{\dfrac{s^2}{\sum(x_i-\bar{x})^2}}$

t統計量

$\dfrac{b}{Std.Error} \qquad$ 自由度=$n-$パラメタ数（単回帰の場合は2）