devianece
fit1とfit2で異なる部分はdevianeceの部分です
逸脱度(deviance) = -2 × 対数尤度
以下はRの出力のまとめです(Rは尤度比検定に必要なNull deviance、Residual devianceを出力します)
Null deviance:切片モデルのdevianceから尤も当てはまりのよいモデル(Full model)のdevianceを引いた値
Residual deviance:回帰モデルのdevianceから尤も当てはまりのよいモデル(Full model)のdevianceを引いた値
| fit1 | fit2 | |
| Null deviance | 43.6268 | 138.59 |
| Null devianceの自由度 | 8 | 99 |
| Residual deviance | 6.3246 | 101.29 |
| Residual devianceの自由度 | 7 | 98 |
| AIC | 30.394 | 105.29 |
この違いから、fit1とfit2では対数尤度が異なることが理解できます
fit1のdeviance
$y_i=$満足の数$、n_i=$患者数$、i=1,2,3, \dotsm ,9$ (ロジスティック回帰 (1)より)
対数尤度
$=L_{\theta1}=log(\prod_{i=1}^{n} (P_i^{y_i}(1-P_i)^{n_i-y_i}))$
$\quad=log(\prod_{i=1}^{9} (P_i^{y_i}(1-P_i)^{n_i-y_i}))$
$\quad=\sum(y_i(\beta_0+\beta_1x_i)-n_ilog(1+e^{\beta_0+\beta_1x_i}))+Const.$
fit1の最大逸脱度
fit1_null <- glm(
cbind(満足, 患者数-満足) ~ 1,
family=binomial,
data=dat1
)
Dmax1 <- -2*logLik(fit1_null)
print(Dmax1)> Dmax1 <- -2*logLik(fit1_null)
> print(Dmax1)
'log Lik.' 63.6964 (df=1)fit1モデルの逸脱度
Dreg1 <- -2*logLik(fit1)
print(Dreg1)> Dreg1 <- -2*logLik(fit1)
> print(Dreg1)
'log Lik.' 26.39419 (df=2)
fit1の最小逸脱度
二項分布より全ての確率から尤度を算出して対数尤度を求めます
Dmin1 <- -2*sum(log(dbinom(dat1$満足, dat1$患者数, dat1$満足/dat1$患者数)))
print(Dmin1)> Dmin1 <- -2*sum(log(dbinom(dat1$満足, dat1$患者数, dat1$満足/dat1$患者数)))
> print(Dmin1)
[1] 20.06961
最大逸脱度と最小逸脱度との差がNull devianceになります
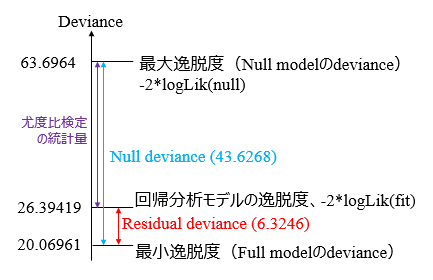
Rでは Null deviance と Residual deviance が算出されます
Null deviance(最大逸脱度$-$最小逸脱度)
Dmax1 - Dmin1> Dmax1 - Dmin1
'log Lik.' 43.62679 (df=1)Residual deviance(回帰分析モデルの逸脱度$-$最小逸脱度)
Dreg1 - Dmin1> Dreg1 - Dmin1
'log Lik.' 6.324581 (df=2)fit2のdeviance
$y_i=$満足の数$(0, 1)、n_i=1、i=1,2,3, \dotsm ,100$
fit2_null <- glm(
cbind(満足, 1-満足) ~ 1,
family=binomial,
data=dat2
)
summary(fit2_null)Call:
glm(formula = cbind(満足, 1 - 満足) ~ 1, family = binomial,
data = dat2)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.04001 0.20004 -0.2 0.841
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 138.59 on 99 degrees of freedom
Residual deviance: 138.59 on 99 degrees of freedom
AIC: 140.59
Number of Fisher Scoring iterations: 3
fit2の最大逸脱度
Dmax2 <- -2*logLik(fit2_null)
print(Dmax2)> Dmax2 <- -2*logLik(fit2_null)
> print(Dmax2)
'log Lik.' 138.5894 (df=1)fit2モデルの逸脱度
Dreg2 <- -2*logLik(fit2)
print(Dreg2)> Dreg2 <- -2*logLik(fit2)
> print(Dreg2)
'log Lik.' 101.2872 (df=2)fit2の最小逸脱度
dat2の場合はグループデータではなく全てのデータが対象となっており対数尤度=0となります
したがって最小逸脱度=0

#回帰分析モデルの逸脱度
-2*logLik(fit2)
#-2*対数尤度からも同じ答えが算出されます
b0 <- summary(fit2)$coef[1, 1]
b1 <- summary(fit2)$coef[2, 1]
print(c(b0, b1))
-2*sum(dat2$満足*(b0+b1*dat2$単位数) - log(1 + exp(b0+b1*dat2$単位数)))> #回帰分析モデルの逸脱度
> -2*logLik(fit2)
'log Lik.' 101.2872 (df=2)
>
> #-2*対数尤度からも同じ答えが算出されます
> b0 <- summary(fit2)$coef[1, 1]
> b1 <- summary(fit2)$coef[2, 1]
> print(c(b0, b1))
[1] -3.6216591 0.1184963
> -2*sum(dat2$満足*(b0+b1*dat2$単位数) - log(1 + exp(b0+b1*dat2$単位数)))
[1] 101.2872AIC(赤池情報量規準: Akaike’s Information Criterion)
$AIC=-2*($最大対数尤度$-$最尤推定したパラメタ数$)$
例)fit1のAIC
-2*(logLik(fit1) - 2)> -2*(logLik(fit1) - 2)
'log Lik.' 30.39419 (df=2)参考文献:久保拓弥. (2012). データ解析のための統計モデリング入門 (Vol. 267). 岩波書店.

