
以前投稿した記事ですのが、そのまま掲載しておきます。ここに記載しているような内容は、ChatGPTなどの対話型AIに尋ねたら詳しく教えてくださいます。
プログラムの最初に入れる関数
Rにcsvファイルを読み込むの準備をご参照ください(Rにcsvファイルを読み込む)
関数
| 密度関数 density | 確率関数 probability | 分位点関数 quantile | |
| t分布 | dt(x, df) | pt(q, df) | qt(p, df) |
| ポワソン分布 | dpois(x, lambda) | ppois(q, lambda) | qpois(p, lambda) |
| 正規分布 | dnorm(x, mean, sd) | pnorm(q, mean, sd) | qnorm(p, mean, sd) |
| 指数分布 | dexp(x, rate) | pexp(q, rate) | qexp(p, rate) |
| F分布 | df(x, df1, df2) | pf(q, df1, df2) | qf(p, df1, df2) |
| カイ二乗分布 | dchisq(x, df) | pchisq(q, df) | qchisq(p, df) |
| 二項分布 | dbinom(x, size, prob) | pbinom(q, size, prob) | qbinom(p, size, prob) |
変数の変換
R
library(tidyr)
dat <- dat %>% mutate(
sexc = factor(sex),
hospc = factor(if_else(hosp == "A病院", 1, 0)),
visit = case_when(
visit == "bdi.pre" ~ 0,
visit == "bdi.2m" ~ 2,
visit == "bdi.3m" ~ 3,
visit == "bdi.5m" ~ 5,
visit == "bdi.8m" ~ 8
)
)点の種類 pch
R
plot(0:25, rep(1, 26),
pch=0:25, cex=2.5,
xlab="", ylab="",
yaxt="n"
)
線
R
x <- c(1, 2, 3)
y <- c(2, 4, 6)
z <- c("p", "l", "o", "b", "c", "h", "s", "S", "n")
par(mfrow = c(3, 3))
for(k in z)plot(x, y, type=k)
par(mfrow=c(1, 1))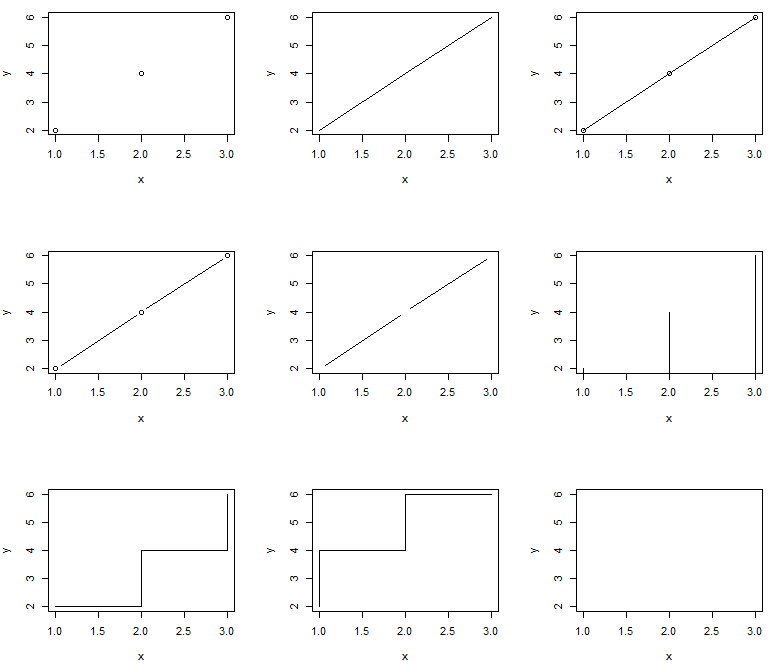
線の種類
R
x <- c(1, 2, 3)
y <- c(2, 4, 6)
par(mfrow=c(3, 3))
for(k in c(0: 6))plot(x, y, type="l", lty=k, lwd=2)
par(mfrow=c(1, 1))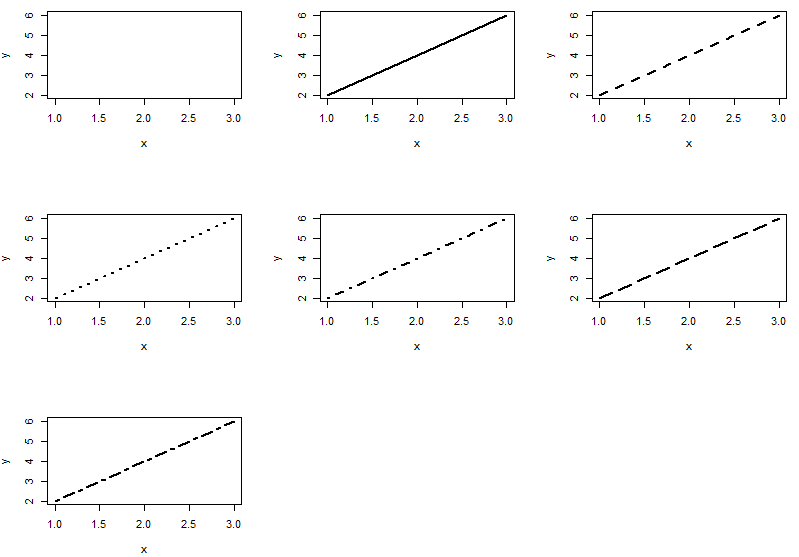
その他の関数
csvファイルの作成
R
write.csv(x, file="ファイル名.csv", fileEncoding="UTF-8")
write.csv(x, file="ファイル名.csv", fileEncoding="Shift-JIS") #日本語含む場合のエンコーディンググラフを2行3列で表示したいとき
最後は1行1列に戻しときましょう
R
par(mfrow=c(2, 3))
#ここにグラフを描く
par(mfrow=c(1, 1))変数を定義するときよく使う関数
以下の変数をdat1に追加する場合
dat1の変数x1を名義変数に変更した変数 x1_cを追加
dat1の変数x2が6の場合には1、他は0とする x2_cを追加
dat1の変数x3が平均以上の場合は1、平均未満の場合は0となる変数 x3_cを追加
dat1の変数x4が10未満の場合は0、10以上の場合は1となる変数 x4_cを追加
R
libraly(dplyr)
dat1 <- dat1 %>% dplyr::mutate(
x1_c=as_factor(x1),
x2_c=if_else(x2==6, 1, 0),
x3_c=if_else(x3>=median(x3), 1, 0),
x4_c=if_else(x4<10, 0, 1)
)回帰直線を引くときに便利
R
#回帰直線
fit <- lm(Y~X, data=dat1 )
round(summary(fit)$coefficients[c(2, 8)],3)
b <- coef(fit)
with(dat1, plot(X, Y, main=""))
xx <- with(dat1, seq(min(X), max(X), length=100))
with(dat1, lines(xx, b[1]+b[2]*xx, lwd=1))# 回帰直線のプロットp値のみを抽出するとき(小数点以下第3位まで)
単回帰
ウィルコクソン
フィッシャー正確検定
t検定
R
fit <- lm(y~x1, data=dat1)
round(summary(fit)$coefficients[c(2, 8)], 3)
round(
wilcox.test(
dat1$"変数1", dat1$"変数2", paired=F, exact=F, alternative="t"
)$p.value, 3
)
round(
fisher.test(
xtabs("データ"~"変数1"+"変数2", data=dat1)
)$p.value, 3
)
round(
fisher.test("分割表")$p.value, 3
)
round(
t.test(
dat1$"変数1", dat1$"変数2"
)$p.value, 3
)変数xを以下の定義に置き換えた変数x_cをdat1に追加する場合
Aの場合、A2
Bの場合、B2
Cの場合、C2
その他は、etc
R
libraly(dplyr)
dat1 <- dat1 %>% mutate(
x_c=dplyr::case_when(
x=="A"~"A2",
x=="B"~"B2",
x=="C"~"C3",
TRUE~"etc"
)
)dat1にあるageを4つにカテゴリー化して、変数age_cを追加します
ageが50未満の場合、50未満
ageが50以上の場合、60未満の場合、50-60
ageが60以上の場合、70未満の場合、60-70
ageが70以上の場合、70以上
R
library(dplyr)
dat1 <- mutate(
dat1, age_c =
if_else(
data$age<50 , "50未満",
if_else(
data$age>=50 & data$age<60, "50-60",
if_else(
data$age>=60 & data$age<70, "60-70",
"70以上"
)))
)
