(2, 3, 6, 7, 10) が確率変数（離散型）の場合
袋の中に 2, 3, 6, 7, 10 の数値が書いてある同じ球が入っています。
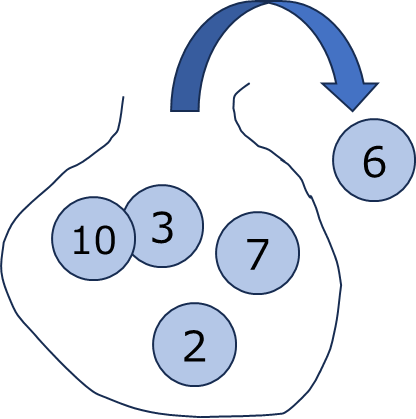
2, 3, 6, 7, 10 を取り出す確率は一定で $\dfrac{1}{5}$ となります。これらの数値は、変数 $X$ の取り得る値であり、$X$ は一様分布（確率分布）に従います。こように確率分布に従う変数のことを確率変数と呼びます。
確率質量関数 $f(x)＝\dfrac{1}{5}$ （離散一様分布）
期待値 $E[X] = \sum{x}*f(x) $
$= 2\frac{1}{5}+3\frac{1}{5}+6\frac{1}{5}+7\frac{1}{5}+10\frac{1}{5}$
$= \dfrac{1}{5}*(2+3+6+7+10)$
sum(x)/5
サイコロの例をよく見かけます「1, 2, 3, 4, 5, 6」
この場合の期待値は $E[X] = \dfrac{N+1}{2}=3.5$ という公式が本やネットで紹介されています。しかしこの公式は、等間隔で並ぶ一連の整数で構成される離散変数のみに当てはまります。今回の例のように不規則な離散変数の場合、期待値は $E[X] = \sum{x}*f(x) $ となります。これはサイコロにも該当するので、$\dfrac{N+1}{2}$ は覚えなくてもよい、いや覚えない方がよいと思います（私見）。
分散 $V[X]$
$V[X]=E\{(X-E[X])^2\}$
$= \sum\{(x-E[X])^2*f(x)\}$
m <- sum(x)/5
sum((x - m)^2)/5
他の求め方
$V[X]=E\{(X-E[X])^2\} = E[X^2]-(E[X])^2$ より
$V[X] = sum(x^2)*\dfrac{1}{10}-(sum(x)*\dfrac{1}{10})^2$
確認
sum(x^2)/5 - (sum(x)/5)^2
下の袋のように、同じ数字が含まれる場合は、確率が異なります。3を取り出す確率は1/3、他は1/6となります。
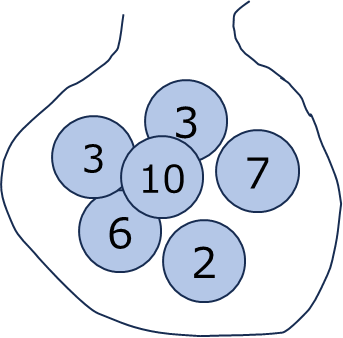
期待値$E[X]$
$E[X] = \sum{x}*f(x) $
exp <- 2*(1/6)+3*(1/3)+6*(1/6)+7*(1/6) + 10*(1/6)
print(exp)
分散$V[X]$
$V[X]=E\{(X-E[X])^2\}$
(2-exp)^2/6 + (3-exp)^2/3 + (6-exp)^2/6 + (7-exp)^2/6 + (10-exp)^2/6 
$V[X]= E[X^2]-(E[X])^2$
2^2/6 + 3^2/3 + 6^2/6 + 7^2/6 + 10^2/6 - exp^2
生成AIも同じ回答ですので、ご安心ください！
(2, 3, 6, 7, 10) が標本の場合
母集団から分析のために選びだされた要素、またはその属性値を標本(サンプル)と呼びます。
標本平均 $\overline{x}= \dfrac{1}{n}\sum(x_i) = \dfrac{ 2 + 3 + 6 + 7 + 10 }{5} = 5.6$
標本分散 $s^2 = \dfrac{1}{n}\sum((x_i-\overline{x})^2) = 8.24$
サンプルは実際の測定値なのですが、確率変数として捉えて期待値（平均値、予測値など）を推定する場合があります。例えば標本平均 $\overline{x}$ は実際の平均なのですが、母集団の平均の推定値（期待値） $E[X]$ として考えることができます。ここでは，標本$( 2, 3, 4, 6, 10 )$が、母集団分布（ 母平均 $\mu$ , 母分散 $\sigma^2$ ）に従う独立な確率変数とします。
標本平均の期待値
標本平均の期待値 $E[ \overline{x} ] = E (\dfrac{2 + 3 + 6 + 7 + 10}{5}) $
$=\dfrac{1}{5}(E(2) + E(3) + E(6) + E(7) + E(10))$
$= \dfrac{1}{5}(\mu+\mu+\mu+\mu+\mu+\mu)$
$= \mu$
つまり 標本平均の期待値 $E[\overline{x}]$ は母平均 $\mu$ に等しい（$E[\overline{x}]=\mu$）。さらに大数の法則による、標本平均 $\overline{x}$ は標本サイズ $n$ が無限に増加するにつれて母平均 $\mu$ に確率的に収束します $((\overline{X} \xrightarrow{P} \mu) \ as \ (n \to \infty))$。
標本平均の分散
$V[ \overline{x}]= V[\dfrac{1}{n}\sum(x_i) ]$
$= V[\dfrac{1}{6}(1 + 2 + 3 + 4 + 5 + 6)]$
$=\dfrac{1}{6^2}(V(1) + V(2) + V(3) + V(4) + V(5) + V(6))$
$=\dfrac{1}{6^2}(\sigma^2 + \sigma^2 + \sigma^2 + \sigma^2 + \sigma^2 + \sigma^2)$
$=\dfrac{\sigma^2}{6}$
$V[ \overline{x}] = \dfrac{\sigma^2}{n}$
標準誤差（SE：Standard Error）
平均値の標準誤差とは「同じ条件で複数回調査と平均値の算出を繰り返した場合の平均値の標準偏差」である
つまりサンプル平均の分散の平方根ということになります
$V[ \overline{x}]=\dfrac{\sigma^2}{n}$ より
$SE = \sqrt{\dfrac{\sigma^2}{n}} = \dfrac{\sigma}{\sqrt{n}}$
生成AI様に尋ねる場合は、「母集団平均a, 母集団分布bから抽出された サンプルx={2, 3, 6, 7, 10} があります。xの平均の期待値と分散を求める考え方と標準誤差の関係について教えてください。」というような質問をしてみてください！
不偏分散
$ s^2 = \dfrac{1}{n-1}\sum_{i=1}^{i=n}({x_i-\overline{x})^2}$
$s^2$ を母分散 $\sigma^2$ の不変推定量、あるいは不偏分散（unbiased variance）という
Rで不偏分散を求める
var(x)
chatGPTに確認してもらいましょう
間違いないようです
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください