
変数 $x_1, x_2, x_3, …$ は、独立同分布(iid: independent and identically distributed)に従って無作為に抽出されたと仮定します。$iid$ ですので、それぞれの期待値を $\mu$ とします。このとき、標本の平均 $\bar{X_n}=\dfrac{1}{n}(X_1+X_2+X_3+…+X_n)$ は サンプルサイズ$(n)$ が大きくなるにつれて $\mu$ に確率収束します。つまり、大数の法則は、$iid$に従う確率変数の平均が、試行回数が増えるにつれてその期待値に収束するという法則です。
例えば、表が出る確率が20%のコインを1枚用意して、数回投げて表が出る確率を記録していく実験をします。この実験を続けて、投げる回数を増やしていくことで表が出る割合はだんだん20%に近づいていきます。
実験1) 表が出る確率20%のコインを10枚投げてみた
表が出る確率20%の同じコインを10枚投げて、表の割合が $0%$ となる確率 $f(0)$ を求めてみます。ここでは二項分布の確率関数を利用して求めることになります。二項分布については以下の記事をご確認ください。
$n:$試行回数(コインの枚数)
$k:$成功回数(表が出る枚数)
$\pi:$コイン自体がもつ表が出る確率
$P(X=k)={}_n C_k\pi^k(1-\pi)^{n-k}$ より
$f_10(0)={}_{10} C_{0}*(\dfrac{1}{5})^0*(1-\dfrac{1}{5})^{10-0}$
f_10_0 <- choose(10, 0) * (1/5)^0 * (1-1/5)^(10-0)
print(f_10_0)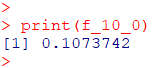
10枚のコインを投げて表の割合が $\dfrac{0}{10}$ となる確率は約11%となります。つまりこの実験を10回繰り返したら、1回は10枚全て裏になるということです。表が0枚となる確率から10枚となる確率まで求めて棒グラフにしてみます。
# 結果を格納するためのベクトルを初期化
f_10 <- c()
# k = 0から10までの値に対して二項確率を求め、結果をベクトルに格納
for (k in 0:10) {
f_10[k + 1] <- choose(10, k) * (1/5)^k * (1-1/5)^(10 - k)
}
# 結果を出力
print(f_10)
# 結果を棒グラフとしてプロット
barplot(
f_10, names.arg = 0:10,
xlab = "表が出た枚数", ylab = "二項確率",
main = "二項分布 (サイズ=10, 確率=1/5)"
)このコードで [k+1] の部分は、ベクトル f_10 のインデックスを指定しています。R言語では、ベクトルのインデックスは1から始まるのに対し、for ループでの k の値は0から始まります。そのため、k の値を直接ベクトルのインデックスとして使用すると、ベクトルの最初の要素にアクセスできなくなります。 [k+1] とすることで、ループの各イテレーションでkが0から10まで変化するとき、ベクトル f_10 のインデックスは1から11までになります。これにより、 の全ての要素(1から11番目)を適切に埋めることができます。f_10
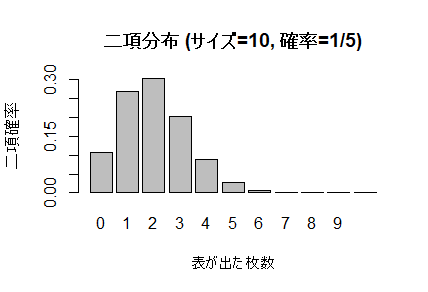
表が2枚(20%)になる確率がやや高くなっていますが、他の枚数もそれなりの確率です。この試行回数を増やことで表割合が20%となる確率が高くなることを以下のシミュレーションで確認してみましょう。
choose(10, k) * (1/5)^k * (1-1/5)^(10 – k) の部分を dbinom(x=k, size=10, prob=1/5) と書き換えても同じ結果が得られます
実験2) 表が出る確率20%のコインを5000枚投げてみた
表が出る確率20%の同じコインの中から必要枚数を取り出します $(iid)$。1枚、10枚、100枚、500枚、1000枚、5000枚を取り出して投げた場合の表が出る確率を求めてみます。現実的な実験ではないのですが、Rを使用することで簡単にシミュレーションできます。成功確率20%の二項乱数からのサンプリングになります。
# 表の確率
p <- 0.20
# コインを投げる枚数(試行回数)
throws <- c(1, 10, 30, 50, 100, 500, 1000, 2000, 3000, 4000, 5000)
# 各枚数についてシミュレーションを実行
# n枚のコイン投げて、表が出る確率を計算
results <- sapply(throws, function(n) {
coins <- rbinom(n, size = 1, prob = p)
mean(coins)
})
# 結果をプロット
plot(throws, results, type = "o", col = "blue",
xlab = "投げたコインの枚数", ylab = "表が出た割合",
main = "")
abline(h = p, col = "red", lty =iid 2)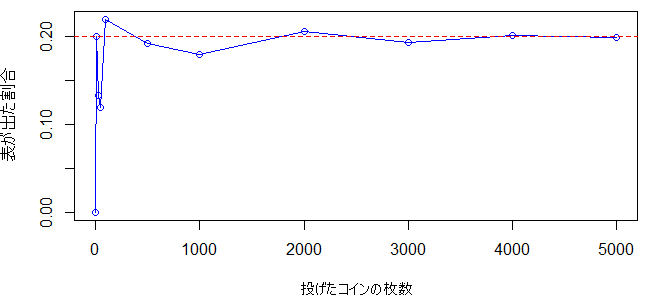
実験3) 表が出る確率20%のコイン1枚を12502500回投げてみた💦
表が出る確率20%のコインを1枚用意します。数回投げてみても20%にはならないときもあります。ところが投げる回数を増やすと、徐々に20%に近づいていきます・・・これが大数の法則でです。1回から5000回まで試行してみて(計12502500回)、それぞれの試行で表が出る確率を記録してみます。実際やったら気が遠くなりそうですが、Rを使ったら簡単にシミュレーションできます。
確率20%の二項乱数を発生させて、1回毎に成功回数(表の回数)を確認します。
# 試行回数を設定
n <- 5000
# 成功確率を設定
p <- 0.20
# 二項乱数を生成 (各試行で1回ずつ、n回試行)
successes <- rbinom(n, size = 1, prob = p)
# 各試行の表の割合
cumulative_means <- cumsum(successes) / (1:n)
# プロット
plot(cumulative_means, type = 'l', ylim = c(0, 1),
xlab = '試行回数', ylab = '表の割合',
main = '')
abline(h = p, col = 'red')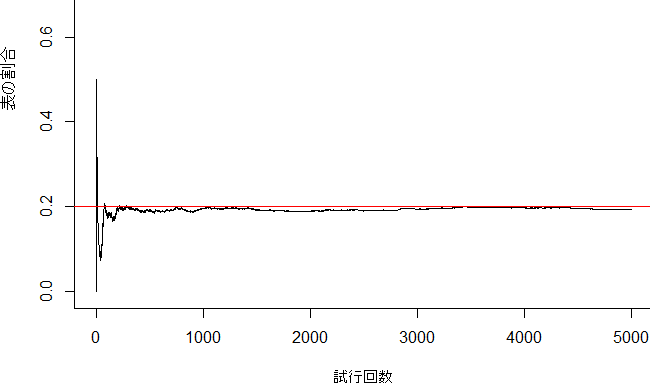
*500回くらいから、かなり安定して20%レベル近くになっているようです。
どの実験も $iid$ からのサンプリングを使用したシミュレーションです。
全ての実験は離散型確率変数に基づいています。
実験2と実験3は、結局同じことを試行しています。


コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください