P値を直接求める方法
サンプルサイズが小さい場合、組合せからｐ値を算出できます
Rの wilcox.test もサンプルサイズが小さい場合には、この方法で算出しているようです（すみません、ChatGPTの情報ですので不確かです。。。）
ChatGPT
wilcox.testで求められる p 値は、特にサンプルサイズが小さい場合には、全ての可能なデータの順位の組み合わせから直接計算されることがあります。これは「正確検定」（exact test）と呼ばれ、統計的検定の精度を高めるために行われます。
（再掲）
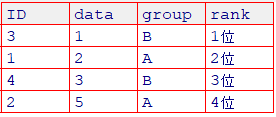
A群(2位, 4位)、A群の順位和 $ W_A=6$
B群(1位, 3位)、B群の順位和 $ W_B=4$
対立仮説1の場合（A群＞B群）
片側検定
全ての可能な組み合わせの中で $W_A≧6$ となる確率
$\dfrac{2}{6}=0.3333$
この考え方は比率の検定をご確認ください
対立仮説2の場合（A群＜B群）
反対側の片側検定
全ての可能な組み合わせの中で $W_A≦6$ となる確率
$\dfrac{5}{6}=0.8333$
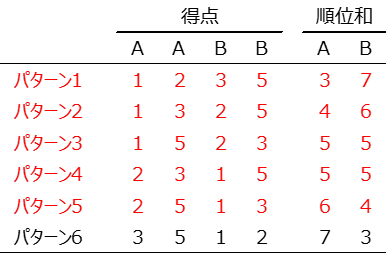
対立仮説3の場合（A群$\ne$B群）
両側検定のp値
A群の順位和≧6または反対側のA群の順位和≦4となる確率
$\dfrac{4}{6}=0.6666$
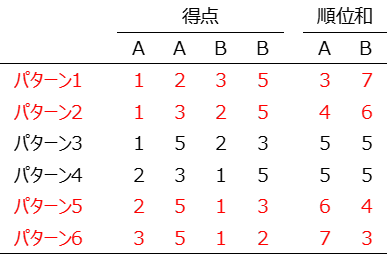
両側検定には、以下のような検定統計量を利用した考え方もあるようですが、ご助言いただける方は、下のコメント欄にご記入いただければ助かります。
ウィルコクソンの順位和検定に使う検定統計量(どちらか一方の順位和)
$W_A=\sum_{i=1}^{n_A}(R_i)$
基準（A群）の順位和の期待値
$E(W_A)=\frac{n_A(n_A+n_B+1)}{2}$
$E(W_A)=\frac{2(2+2+1)}{2}=5$
A群の順位和（実測値）と期待値との差：$6-5=1$
差が $1$ になるような、反対側の順位和は、$4$ (5-4=1)
両側検定のｐ値 ＝ A群の順位和≧6または反対側のA群の順位和≦4となる確率
正規近似による方法
データの準備と要約
data <- c(
12, 4, 9, 6, 2, 10, 12, 11, 7, 10,
10, 10, 25, 13, 18, 7, 15, 9, 18, 19)
group <- c(rep("X",10), rep("Y",10))
dat_xy <- data.frame(data, group)
#View(dat_xy)
順位を追加
#dataの順位列 (rank) を追加
dat_xy2 <- dat_xy %>%
mutate(rank = rank(data, ties.method = "average"))
#順位でソート
dat_xy3 <- dat_xy2 %>%
arrange(rank)
#View(dat_xy3)
片側検定（帰無仮説Y群>X群）
ここからは、coinパッケージのwilcox_testを使用します
#groupをファクター変数に変更してYを基準に変更
dat_xy$group <- factor(dat_xy$group)yを基準にして片側検定
dat_xy$group <- relevel(dat_xy$group, ref="Y")
coin::wilcox_test(
data ~ group,
data = dat_xy,
alternative = "greater"
)
有意水準5％のもとで、YはXより優位に高いことが分かりました
コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください