比率の検定（1標本問題：10人中\(k\)人が転倒した町）

下側検定

ここからは例題が変わります。今度は私が想定した「10名中１名が転倒経験のあるT町」について考えます。実存しない架空の例題です。

例題 2
「85歳以上」では25.3％と4人に1人の割合で転倒することが報告されています（内閣府）。この確率25.3％を転倒が起こる確率、つまり目的としている結果が起こる確率 pとして進めます。T町に在住する85歳以上の高齢者から無作為に選んだ10名に調査した結果、1名が転倒経験ありという結果だった。T町の転倒割合は、全国割合（25.3％）より小さいと言えるか、有意水準5％で検証せよ。

・帰無仮説：T町の転倒割合は、全国割合（25.3％）に等しい
・対立仮説：T町の転倒割合は、全国割合（25.3％）より小さい

ある比率より小さいことを実証した場合には、下側検定を実施します（ここ重要）。もうお分かりかと思いますが、以下の青色部分の検定になります。検定をしなくても確率関数のグラフからP値は0.2より大きくなることがわかります。

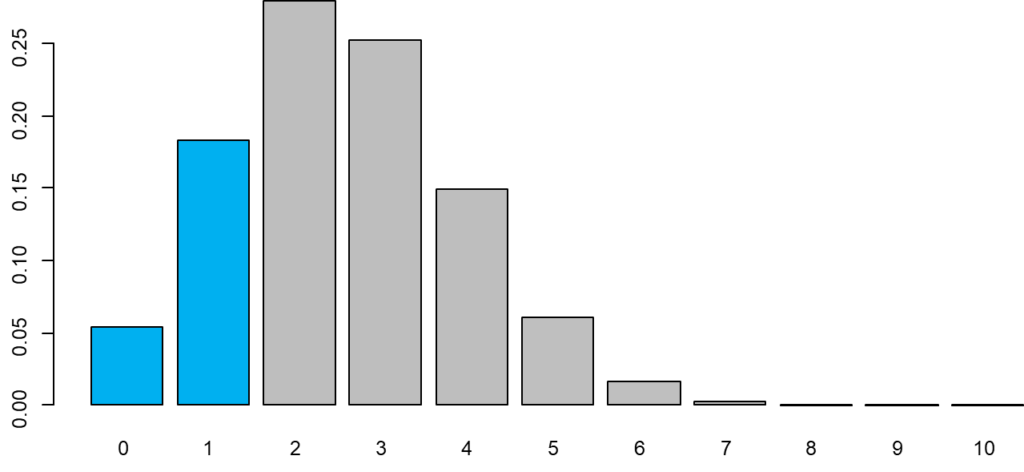
つまりT町の転倒割合は、全国割合（25.3％）より小さいとは言えません

Rを使って求めてみます

binom.test(
    x=1, n=10, p=0.253,
    alternative="less"
)

下側検定なので alternative = “less”。P値=0.237で、やはり有意な結果は得られませんでした。

P値

上述した検定結果のP値のみを算出する場合

pbinom(
    q=1, size=10, prob=0.253,
    lower.tail=T
)

転倒割合は10％のままで、サンプルサイズと転倒回数を増やしてみましょう。これは少し多めにしないとp値は小さくならないでしょう…ｎ＝40、転倒4回くらいでどうでしょうか。

t <- 0:40

p <- dbinom(
    x=t, size=40, prob=0.253
)

barplot(
    p~t, pch=16, xlab="", ylab=""
)

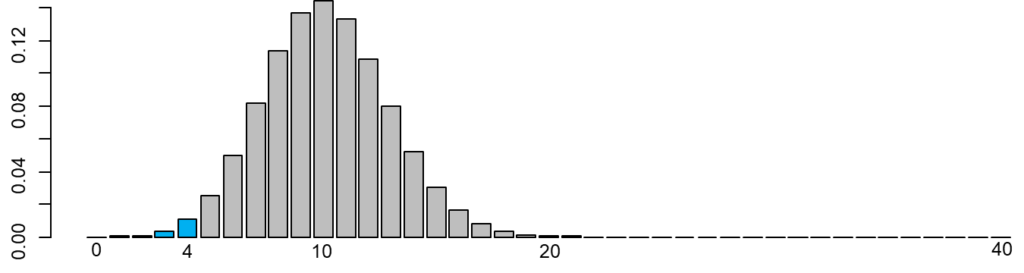
これはp<0.05になっているのではないでしょうか

pbinom(
    q=4, size=40, prob=0.253,
    lower.tail=TRUE
)

有意になりました

サンプルサイズを増やすことが重要なのはよく分かるのですが、忙しいリハ業務のなかでサンプルサイズは簡単に増やせませんよね・・・？。だから、サンプルサイズの小さい研究では、95％信頼区間がより重要になります。

両側検定

95%信頼区間の前に両側検定について架空の例題で説明しておきます。

Rでは両側検定がデフォルト設定になっています。つまり、何も指定しなければ両側検定になります（alternative = “two.sided” ）。

例題 3
U町に在住する85歳以上の高齢者から無作為に20名抽出して調査した結果、7名が転倒経験ありという結果だった。T町の転倒割合は、全国割合（25.3％）とは異なることを証明したい。

・帰無仮説　T町の転倒割合は、全国割合（25.3％）に等しい
・対立仮説　T町の転倒割合は、全国割合（25.3％）とは異なる

Rでやってみましょう。まず、確率分布のグラフを描いておきます。

t <- 0:20

p <- dbinom(
    x=t, size=20, prob=0.253
)

barplot(
    p~t, pch=16, xlab="", ylab=""
)

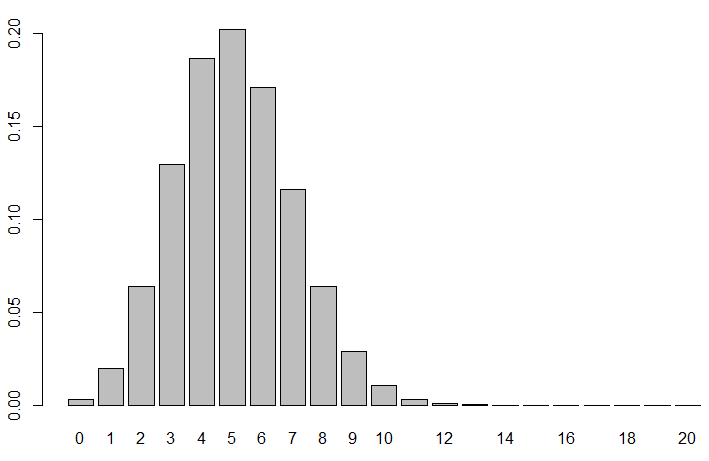
二項検定を行います。alternative = “two.sided” はデフォルトなので書く必要はありませんが、間違うこともありますので、丁寧に記載しておきましょう。

binom.test(
    x=8, n=20, p=0.253,
    alternative="two.sided"
)

P=0.1943で帰無仮説は棄却できません。したがって全国平均とは有意に異なることが言えませんでした。このP値の求め方を勉強しましょう。

両側検定のP値を求めるための3つの方法

二項分布とベルヌーイ分布

リハビリテーション統計学に必須の確率分布です。地域Aの「週に1回以上の頻度で運動する人の割合」を50％とします. この地域からお互いに全く関係のない3名（Aさん、Bさん、Cさん）をランダムに選んで実施した二者択一のアンケート結果から確率を求めてみましょう・・・？

y2pt.com

2023.01.01

その1　

P値の２倍（上側検定または下側検定の小さい方のp値を使用する）

pbinom(
    q=7, size=20, prob=0.253,
    lower.tail=FALSE
)*2

$q=7$となるので注意してください。lower.tail = FALSEなのでq ≦ 7を含まない、つまりq ≧8となります （離散型）。

その2

｜期待値ー観測された割合｜以上となる確率の合計

期待値：\(np = 20*0.253 = 5.06\)

\((|k – 5.06|) ≧ (|8-5.06|) =2.94 \)となる\(P(k)\)

\(k = 8, 9, …, 20\)

\(k = 2, 1, 0\)

pbinom(
    q=7, size=20, prob=0.253,
    lower.tail=FALSE) +
pbinom(
    q=2, size=20, prob=0.253,
    lower.tail=TRUE
)

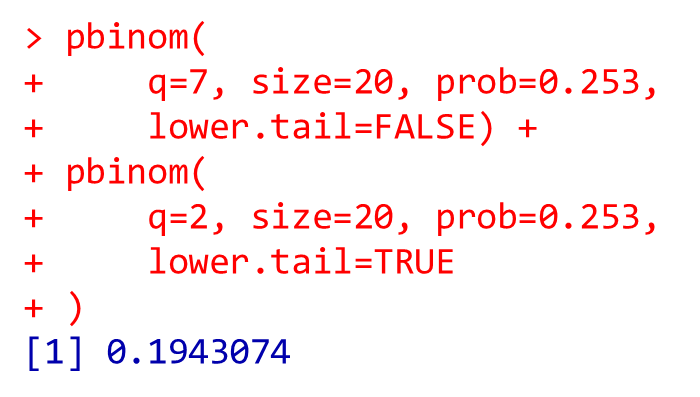
lower.tail = TRUEの場合、なのでq≦3を含む、つまりq≦3となります

その3

確率が \(P(8)\) 以下となる確率の合計

Rはこの方法でP値を算しています

dbinom(
    x=8, size=30, prob=0.253
) 

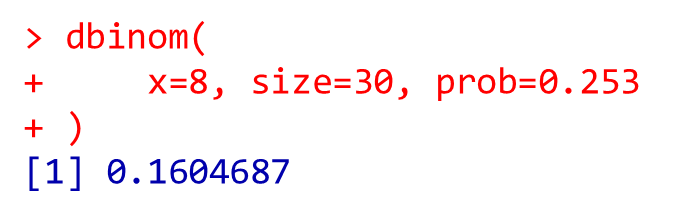
$P(8) = 0.16$なので

$P(k | P(k) ≦ 0.16 )$　を求めます

$k = 8, 9, …, 20$

$K = 2, 1, 0$

pbinom(
    q=7, size=20, prob=0.253,
    lower.tail=FALSE) + 
pbinom(
    q=2, size=20, prob=0.253,
    lower.tail=TRUE
)

今回はその2とその3は同じ値になりましたが、異なる場合もあります。