比率の検定（1標本問題：10人中\(k\)人が転倒した町）

その3

確率が \(P(8)\) 以下となる確率の合計

Rはこの方法でP値を算しています

dbinom(
    x=8, size=30, prob=0.253
) 

$P(8) = 0.16$なので

$P(k | P(k) ≦ 0.16 )$　を求めます

$k = 8, 9, …, 20$

$K = 2, 1, 0$

pbinom(
    q=7, size=20, prob=0.253,
    lower.tail=FALSE) + 
pbinom(
    q=2, size=20, prob=0.253,
    lower.tail=TRUE
)

今回はその2とその3は同じ値になりましたが、異なる場合もあります。

95%信頼区間

今回の調査はサンプルサイズが非常に小さかったのですが、この調査をもし100回行ったとすれば、今回の結果がどの程度の範囲に入るのでしょうか

これは確率ではありません（間違いやすいので注意が必要です）

95%信頼区間とはこの調査を100回繰り返した場合に95回が収まるであろう区間のことです

例題
「85歳以上」では25.3％と4人に1人の割合で転倒することが報告されています（内閣府）。この確率25.3％を転倒が起こる確率、つまり目的としている結果が起こる確率として進めます。S町に在住する85歳以上の高齢者から無作為に10名抽出して調査した結果、5名が転倒経験ありという結果だった。この場合の95％信頼区間を求めよ！

Rで実際に二項検定で求めてみましょう

binom.test(
    5, n=10, p=0.253
)

95％信頼区間は0.187～0.813となりました

今回の割合は50％だったのですが、同じ調査を100回繰り返したとしたら、95回は18.7%～81.3%の範囲に収まるという推定結果です。

どうでしょうか？

ｐ値は有意ではなかったのですが、25.3％が信頼区間のかなり端の部分に位置していることが理解できます

有意差の有無よりも95％信頼区間を提示することが重要ですね

95％信頼区間の求め方

F分布を利用した求め方 (Clopper-Pearsonの信頼区間)

自由度

\(u1=2*(n-i+1)\)、 \(u2=2*i\)

\(l1=2*(i+1)\)、 \(l2=2*(n-i)\)

\([\frac{u2}{u2+u1F_{1-0.025}(u1, u2)}\),\(\ \ \frac{l1F_{1-0.025}(l1, l2)}{l2+l1F_{1-0.025}(l1, l2)}]\)

X～B(n, 0.253)の場合の上側P値

\(P(X≧i) = P(F_{(u1, u2)} ≧ \frac{u2(1-π)}{u1*π} )\)

\(π=\frac{u2}{u2+u1F_{1-0.025}(u1, u2)}\)

n = 10
i = 5
u1 <- 2 * (n-i+1)
u2 <- 2 * i
(π = u2 / (u2 + u1*qf(0.975, u1, u2)))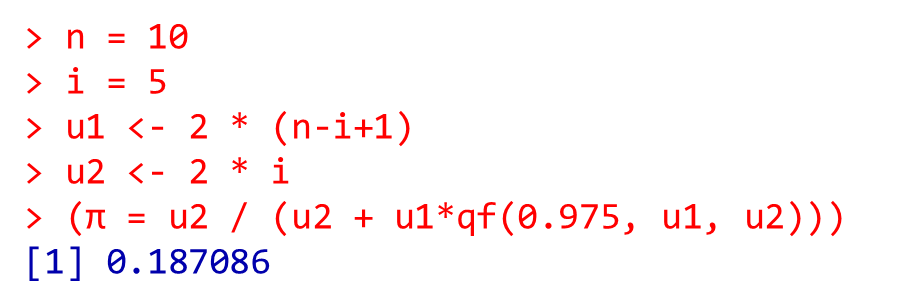

X～B(n, 0.253)の場合の下側P値

\(P(X≦i) = P(F_{(l1, l2)} ≦ \frac{l2*π}{l1*(1-π)})\)

\(π=\frac{l1F_{1-0.025}(l1, l2)}{l2+l1F_{1-0.025}(l1, l2)}\)

n = 10
i = 5
l1 <- 2 * (i+1)
l2 <- 2 * (n-i)
(π = l1 * qf(0.975, l1, l2) / (l2 + l1*qf(0.975, l1, l2)))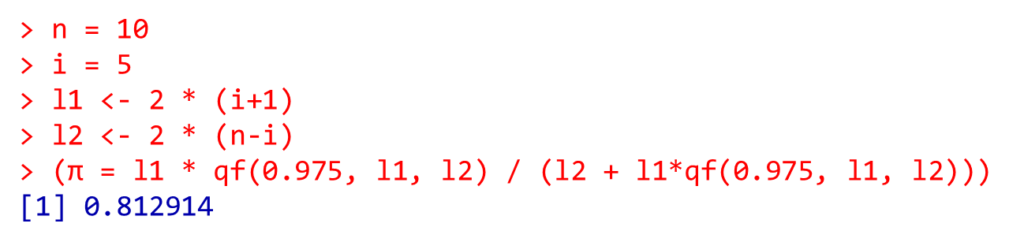

binom.testで出た結果と同じ値になりました

正規近似による求め方

次に正規分布に近似させる方法で求めてみましょう

近似ですのでF分布ほど厳密な方法ではありません

二項分布の期待値\(nπ\)、 分散\(nπ(1-π)\)より

\(E[\frac{i}{n}] = π\)

\(V[\frac{i}{n}] = \frac{1}{n^2}V[ i ] = \frac{1}{n^2}nπ(1-π)\)

\(X～N(π, \frac{π(1-π)}{n})\)

母比率Pの検定では帰無仮説H0=P=πとすると、この仮説のもとzは近似的に標準正規分布に従う

\(z = \frac{P-π}{\sqrt{\frac{π(1-π)}{n}}}\)

信頼区間

\(\frac{i}{n} ± z(1-0.025)\sqrt{(\frac{\frac{i}{n}(1-\frac{i}{n})}{n})}\)

Rで書くと以下のようになります

n = 10
i = 5
p1 = 0.5
p0 = 0.253
#Z統計量 N(0, 1)
z <- abs(p1-p0) / sqrt(p0*(1-p0)/n)
(p = p1 + c(-1, 1) * z * 0.975 * sqrt(p1*(1-p1)/n))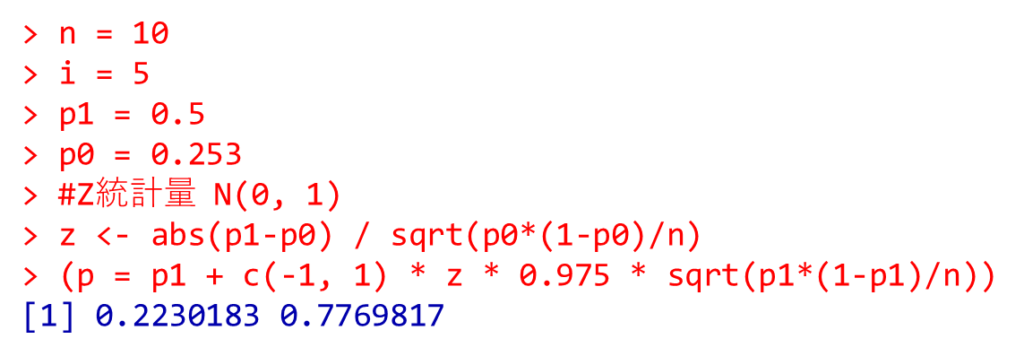

nが小さいので補正を行ってみます（Yatesの連続補正）

n = 10
il = 1 + 0.5 #i+0.5補正
iu = 1 - 0.5 #i-0.5補正
pl = 0.15
pu = 0.05
p = 0.253
#下限
z <- abs(pl-p) / sqrt(p*(1-p)/n)
pl - z * 0.975 * sqrt(pl*(1-pl)/n)
#上限
z <- abs(pu-p) / sqrt(p*(1-p)/n)
pu + z * 0.975 * sqrt(pu*(1-pu)/n)

F分布で求めた信頼区間に近づきました

サンプルサイズが小さいので信頼区間の幅もかない大きくなっています

F分布

血圧測定した結果、A群50名の分散10mmHg, B群30名の分散5mmHgであった。A群とB群の母分散は等しいと言えるか？F分布はリハビリテーション統計学の検定で頻出する確率分布です。

y2pt.com

2023.01.01

サンプルサイズの設計

例題
「85歳以上」では25.3％と4人に1人の割合で転倒することが報告されています（内閣府）。1標本における比率の検定を行う場合、誤差を5％以内に収めるためには、どのくらいのサンプルが必要となるでしょうか？

つまり95％信頼区間が±0.05の範囲に収まるようなサンプルサイズということになります

上述した正規近似を利用して求めてみましょう

信頼区間

\(1.96\sqrt{\frac{0.253(1-0.253)}{n}}=0.05\)となるようなnを求めます

n=290程度あれば誤差の少ない信頼区間が推定できそうですが、290も無理ですよね・・・

n=290程度あれば誤差の少ない信頼区間が推定できそうですが、n=290は無理ですよね・・・

参考文献