
データの準備と要約
サンプル(RにCSVファイルを読み込むをご覧ください)
サンプルデータのnormal_50は平均50、分散100の標準正規分布からの乱数100個です
サンプルデータをdatに格納します
dat <- read.csv("normal_50.csv", header=T, fileEncoding = "UTF-8")使用するパッケージ(パッケージのインストール)
library(ggplot2)
library(ggpubr)箱ひげ図
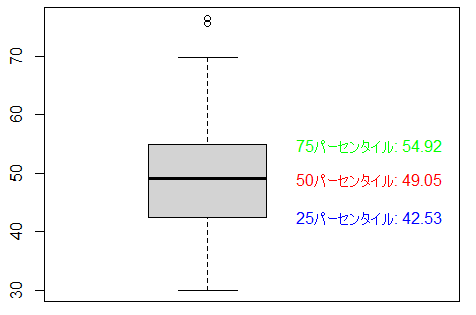
#箱ひげ図
boxplot(
dat$data, at=0.5,
main="箱ひげ図",
ylab="", xlab="",
xlim=c(0,1.3)
)
# 四分位数を計算
quantiles <- quantile(dat$data)
# 四分位数をプロットにテキストとして追加(x座標を調整して右側に移動)
text(
x = 0.8, y = quantiles[2],
labels = paste("25パーセンタイル:", round(quantiles[2], 2)),
col = 'blue', adj=0
)
text(
x = 0.8, y = quantiles[3],
labels = paste("50パーセンタイル:", round(quantiles[3], 2)),
col = 'red', adj=0
)
text(
x = 0.8, y = quantiles[4],
labels = paste("75パーセンタイル:", round(quantiles[4], 2)),
col = 'green', adj=0
)Q-Q プロット(Quantile-Quantile plot)
確率密度関数
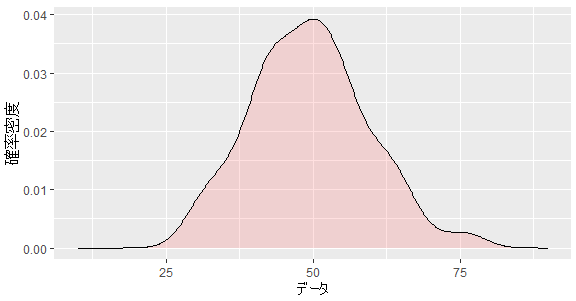
ggplot(dat, aes(x = data)) +
geom_density(alpha = .2, fill = "#FF6666") +
labs(title = "", x = "データ", y = "確率密度")+
scale_x_continuous(limits = c(10, 90)) サンプルがもし平均0、標準偏差1の正規分布の場合、データ=Zスコアとなります。詳しくは以下のページをご確認ください。
累積分布関数
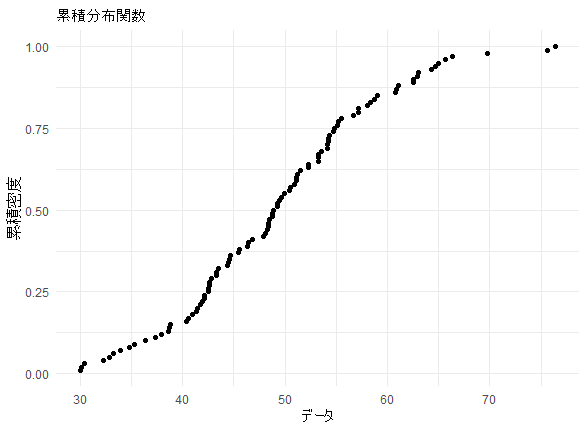
# 累積分布関数のデータフレームを作成
cdf_data <- ecdf(dat$data)(dat$data)
cdf_frame <- data.frame(x = dat$data, cdf = cdf_data)
# 累積分布関数のグラフを描画
ggplot(cdf_frame, aes(x = x, y = cdf)) +
geom_point() +
labs(title = "累積分布関数", x = "データ", y = "累積密度") +
theme_minimal()確率密度関数(Probability Density Function、PDF)は、連続確率分布の確率変数の密度を示します。
確率質量関数(Probability Mass Function, PMF)は、離散確率分布における各値の確率を示します。
累積分布関数(Cumulative Distribution Function, CDF)は、確率変数が特定の値以下になる確率を表します。CDFは連続および離散の両方の確率分布に対して定義されます。
正規確率紙にプロット
y軸のメモリはzスコアに対応する累積密度となっています。サンプルデータの場合、y軸の50パーセンタイルはzスコアが 50 に対応しており、75パーセンタイルはzスコアが 56.7449 に対応しています。この変換により、Y軸の中央付近は密で、端の方は間隔が広がります。これは、正規分布の確率密度が中央付近で高く、端に行くほど低くなるのが原因です。プロット全体が直線に近い位置にある場合、それはデータセットが正規分布に従っていることを視覚的に示すことになります。正規確率紙は、データの正規性を評価するための非常に有効なツールです。
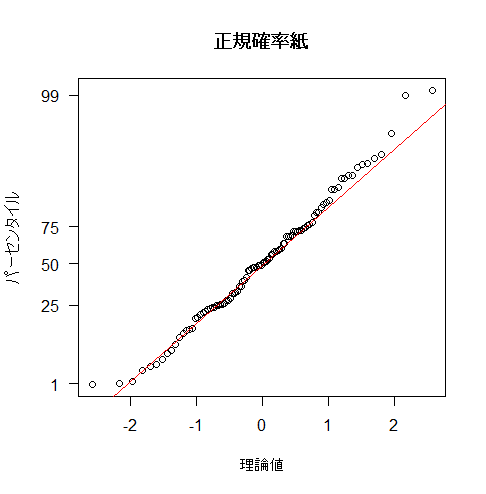
# 例としてnormal_50データセットのdata列を使用
data <- dat$data
# 正規確率プロットを作成(y軸のラベルとティックを非表示にする)
qqnorm(data, main = "正規確率紙", ylab = "パーセンタイル", xlab = "理論値", yaxt = "n")
qqline(data, col = "red")
# 指定されたパーセンタイルの計算
perc_at <- c(0.01, 0.25, 0.5, 0.75, 0.99)
perc_labels <- c("1", "25", "50", "75", "99") # 対応するパーセンタイルのラベル
# y軸のティックマークとラベルを更新
axis(2, at = quantile(data, probs = perc_at), labels = perc_labels, las = 1)
Q-Qプロットの描き方
QQプロットは、サンプルデータの分位数と、特定の理論分布(例えば正規分布)の分位数を比較することで作成されます。X軸には理論分布の分位数(Theoretical Quantiles)を、Y軸にはサンプルデータの分位数(Sample Quantiles)を表示します。正規分布を例に取ると、X軸の理論分位数は正規分布のzスコアに対応します。この比較を通じて、サンプルデータが選択した理論分布にどの程度従っているかを視覚的に評価できます。もしデータが理論分布に良く従っているなら、プロット上の点は直線状に配置されます。
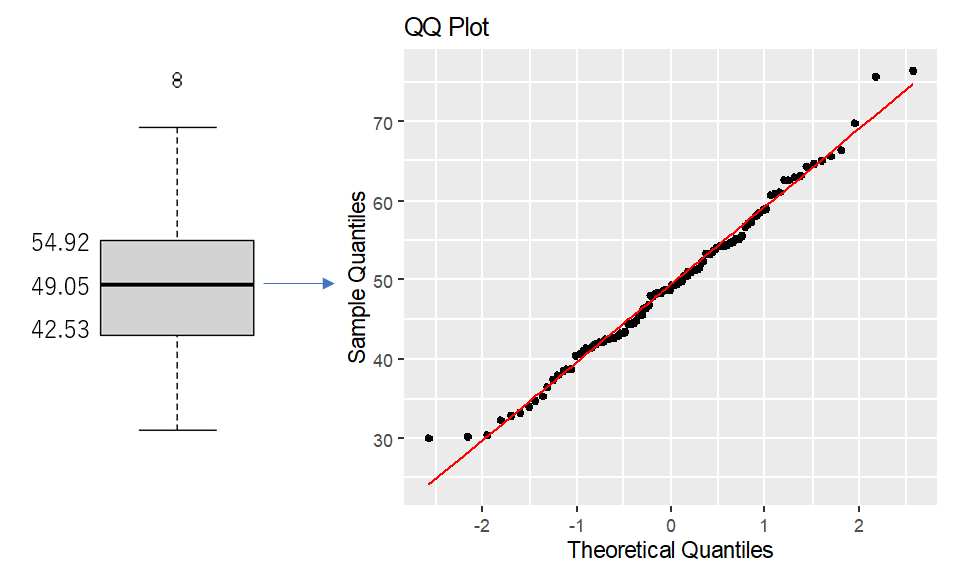
sorted_data <- sort(dat$data)
# 分位数を計算
n <- length(sorted_data)
probs <- ppoints(n) # 等間隔の確率を生成
theoretical_quantiles <- qnorm(probs)
# 正規確率プロットを作成
ggplot() +
geom_point(aes(x = theoretical_quantiles, y = sorted_data)) +
geom_line(aes(x = theoretical_quantiles, y = theoretical_quantiles * sd(sorted_data) + mean(sorted_data)), color = "red") +
xlab("Theoretical Quantiles") +
ylab("Sample Quantiles") +
ggtitle("QQ Plot")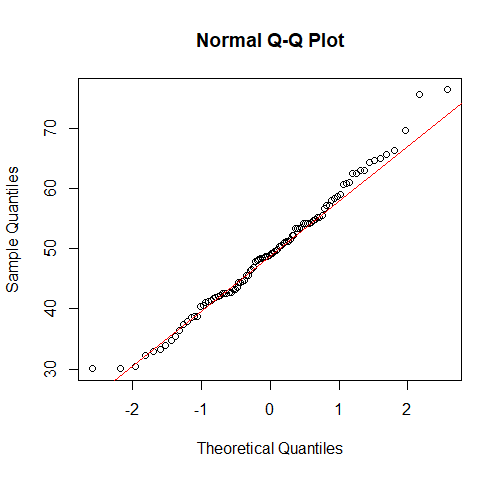
簡単に描く方法(qqnorm関数)
qqnorm(dat$data)
qqline(dat$data, col = "red")理解を深めるために qqnorm関数 を使用しない描き方も載せておきます(上図と同じ図になります)
# y軸のデータ作成
# データを昇順にソート
data <- dat$data
sorted_data <- sort(data) #
#x軸のデータ作成
# 分位数を計算 (プロットのための分位数)
n <- length(sorted_data)
probs <- ((1:n) - 0.5) / n
#データが正規分布なのでZスコアを求めます
quantiles <- qnorm(probs)
# データの分位数と理論分位数をプロット
plot(
quantiles, sorted_data,
main="QQ Plot",
xlab="Theoretical Quantiles",
ylab="Sample Quantiles"
)
# 直線を追加(データが正規分布に従う場合)
abline(lm(sorted_data ~ quantiles), col="red")指数分布を仮定したQ-Qプロット
指数分布から生成した乱数を使用して、QQプロットで評価してみましょう。理論分布を正規分布としてプロットしたら大きく逸脱します。
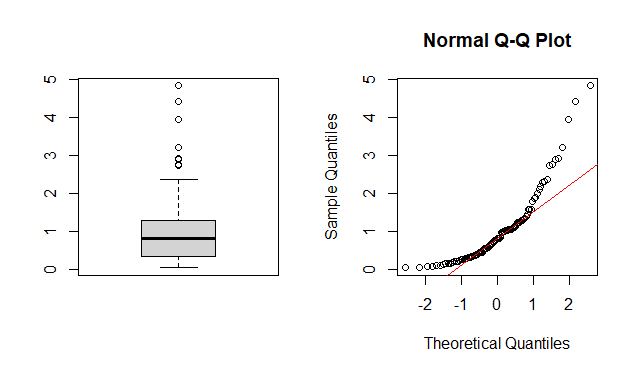
# 指数分布からの乱数を生成
set.seed(0)
# rate = 1 の指数分布
data2 <- rexp(100, rate = 1)
# 正規確率プロットを作成
par(mfrow = c(1, 2))
boxplot(data2)
qqnorm(data2)
qqline(data2, col = "red")
par(mfrow=c(1, 1))理論分布に指数分布を設定してQQプロットを作成することで直線状に位置します。これで指数分布から逸脱していないことが評価できます。

# 指数分布の分位数関数を取得
exp_quantiles <- function(p) {
qexp(p, rate = 1) # qexpは指数分布の分位数関数
}
# 理論分布とサンプルデータとのQ-Qプロットを描く
qqplot(
exp_quantiles(ppoints(length(data2))),
data2,
main = "Exponential Q-Q Plot",
xlab="データ", ylab="")
abline(0, 1, col = "red") # y = x の直線を赤色で追加丹後 俊郎 (編集), 松井 茂之 (編集); 医学統計学ハンドブック, 朝倉書店; 新版, 2018, pp45-46

