
データの準備と要約
使用するパッケージ(パッケージのインストール)
library(ggplot2)
library(dplyr)
データセット unif をdatに格納します(ファイルの読み込み).
サンプルデータの取り込み
setwd("C:\\Users\\rehay\\Documents\\back up folder\\統計学備忘録\\ブログで使用したサンプル")
getwd()
.libPaths("C:\\Users\\rehay\\Documents\\Rpackages")
dat <- read.csv("unif.csv", header=T, fileEncoding = "UTF-8")
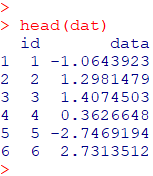
head(dat)
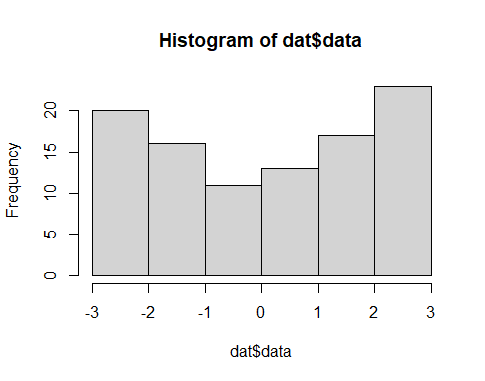
hist(dat$data)
サンプルデータの unif は一様分布からの乱数です
検定
データセット unif についてKolmogorov-Smirnov 検定(コルモゴロフ・スミルノフ検定)とShapiro-Wilk検定を実行します。
帰無仮説:サンプルデータは指定された理論分布(ここでは正規分布)に従う
有意水準:5%
1標本のKolmogorov-Smirnov 検定(KS検定)
y=”pnorm” で正規分布を指定します
ks.test(
x=dat$data, y="pnorm",
mean=mean(dat$data),
sd=sd(dat$data)
)

p>0.05より、データが正規分布に従うという帰無仮説を棄却するには十分ではありません。従って「サンプルデータは正規分布から有意に逸脱しているとは言えない」という結果になりました。
2標本のKolmogorov-Smirnov検定では、2つのサンプルが同じ分布から抽出されたかどうかを検定します。異なるサンプルセットが同じ分布特性を持つかどうかを評価することができます。
Shapiro-Wilk検定
shapiro.test(x=dat$data)
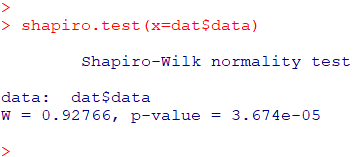
p<0.05より、データが正規分布に従うという帰無仮説が棄却されます。従って「サンプルデータは正規分布から有意に逸脱している」と考えられます。
Kolmogorov-Smirnov検定とShapiro-Wilk検定では判定が異なります。ヒストグラムを見た限りでは、正規分布ではないようですので、Shapiro-Wilk検定が正しいようです。
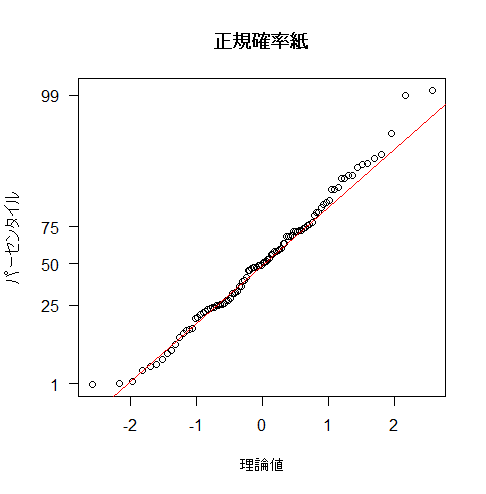
Kolmogorov-Smirnov検定やShapiro-Wilk検定などの正規性検定は、小さなサンプルサイズの場合、第一種の過誤(帰無仮説を誤って棄却すること)を犯す確率が高まる傾向があります。また、サンプルサイズが大きくなると、わずかな正規性からの逸脱も検出する可能性があります。正規性を評価する場合は、上述した検定だけではなく、ヒストグラムやQQプロット(Quantile-Quantileプロット)などのグラフィカルな評価も必須です。
統計量
KS検定の統計量
KS検定には1標本と2標本の検定があります. ここでは正規分布との比較になりますので、1標本のKS検定を紹介します.
1標本のKS検定では、2つの累積分布関数の間の最大差異を統計量(D統計量)として使用します。サンプルの分布が特定の理論分布(正規分布など)に従っているかをD統計量から検定します。
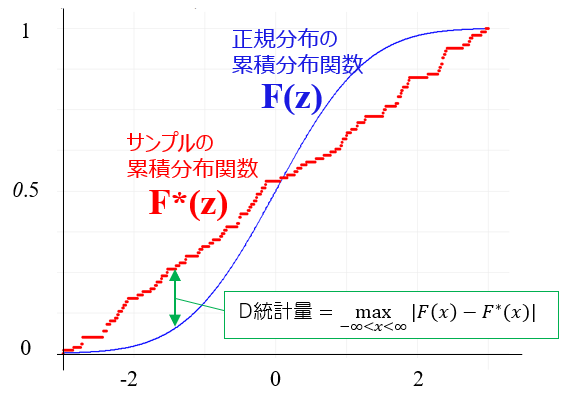
この図の描き方
# 標準正規分布からの累積密度関数(CDF)を計算
x_values <- seq(-3, 3, by = 0.01)
normal_cdf <- pnorm(x_values)
# 一様分布からサンプルデータを生成し、経験的CDFを計算
sample_cdf <- ecdf(dat$data)(x_values)
# データフレームの作成
normal_df <- data.frame(
x = x_values, cdf = normal_cdf, Distribution = 'Normal CDF')
sample_df <- data.frame(
x = x_values, cdf = sample_cdf, Distribution = 'Sample CDF')
# ggplotを使用してグラフを描画
ggplot() +
geom_line(
data = normal_df,
aes(x = x, y = cdf, color = Distribution), size = 1) +
geom_point(
data = sample_df,
aes(x = x, y = cdf, color = Distribution), size = 1.5) +
labs(title = "Comparison of Normal CDF and Sample CDF",
x = "Value",
y = "Cumulative Density") +
theme_minimal() +
scale_color_manual(
values = c("Normal CDF" = "blue", "Sample CDF" = "red"))
KS検定は,サンプルデータが理論分布の累積分布関数 $F(z)$ に従うかどうかを検定する方法です. 上図では理論分布を正規分布としています. 実際に得られたデータから作成された経験的累積分布関数 $F^*(z)$ とし、正規分布の累積分布関数 $F(z)$ との乖離を以下の検定統計量Dで評価することになります.
$D= \displaystyle \max_{-\infty<x<\infty}|F(x)-F^*(x)|$
帰無仮説: $F^*(x)$ が $F(x)$ に一致する
帰無仮説のもとで $\sqrt{n}D$ は以下の分布に従うことが知られています
$P(\sqrt{n}D \le x)$
$=1-2\sum_{i=1}^\infty(-1)^{i-1}exp(-2i^2x^2)$
$=\dfrac{\sqrt{2\pi}}{x}\sum_{i=1}^\infty exp(-\dfrac{(2i-1)^2\pi^2}{8x^2})$
$n:$ サンプルサイズ
$x:$ 統計量の特定の値
$i:$ 無限級数の各項
Shapiro-Wilk 検定の統計量
Shapiro-Wilk検定の統計量 $W$ は、サンプルデータ $x_i$ の順序統計量と標準正規分布に従う確率変数の順序統計量の期待値の関係を利用します
順序統計量
データセット $y$ から順序統計量を計算します。これは、データセットを小さいものから大きいものへと順序付けしたものです。
$y_i =(y_1, y_2, \dotsc , y_n) \quad y_1 \leq y_2 \leq \dotsc \leq y_n$
期待値と共分散行列
標準正規分布に従う確率変数の順序統計量の期待値 $m$ と共分散行列 $V$ を定義します。 $m_i$ は $i$ 番目の順序統計量の期待値、$v_{ij}$ は $i$ 番目と $j$ 番目の順序統計量の共分散。
$m=(m_1, m_2, \dotsc ,m_n)$
$V=(v_{ij})$
$V$ の分散共分散行列の求め方は以下の文献をご参照ください
- Royston, J. P. (1982). Algorithm AS 177: Expected normal order statistics (exact and approximate). Journal of the royal statistical society. Series C (Applied statistics), 31(2), 161-165.
- Davis, C. S., & Stephens, M. A. (1978). Approximating the covariance matrix of normal order statistics. Journal of the Royal Statistical Society: Series C (Applied Statistics), 27(2), 206-212.
重み
共分散行列 $V$ の逆行列 $V^{-1}$、期待値 $m$ の転置ベクトル $m^T$ を用いて重みベクトル $(a_1, a_2, \dotsc , a_n)$ を計算します。この重みは、サンプルデータの順序統計量と正規分布の順序統計量を関連付けるためのものです。検定統計量を計算する際に、サンプルデータが正規分布にどの程度近いかを測定するために用いられます。
共分散行列 $V$ の逆行列 $V^{-1}$、期待値 $m$ の転置ベクトル $m^T$ を用いて重みベクトル $(a_1, a_2, \dotsc, a_n)$ を計算します。この重みは、サンプルデータの順序統計量と正規分布の順序統計量を関連付けるためのものです。検定統計量を計算する際に、サンプルデータが正規分布にどの程度近いかを測定するために用いられます。
$(a_1, a_2, \dotsc , a_n) = \dfrac{m^TV^{-1}}{\sqrt{m^TV^{-1}V^{-1}m}}$
統計量
重み付けされたサンプルデータの線形結合の平方を、サンプルデータの分散で割ることで統計量 $W$ を計算します。これは、サンプルデータがどの程度正規分布に近いかを示す値になります。
$W=\dfrac{(\sum_{i=1}^na_iy_i)^2}{\sum_{i=1}^n(y_i- \bar{y})^2}$
- 丹後 俊郎 (編集), 松井 茂之 (編集); 医学統計学ハンドブック, 朝倉書店; 新版, 2018, pp45-46
- 坂巻顕太郎, 篠崎智大(監修); 生物統計学の道標 研究デザインから論文報告までをより深く理解するための24講, 一般財団法人 厚生労働統計協会, p153
- Rochon, J., Gondan, M., & Kieser, M. (2012). To test or not to test: Preliminary assessment of normality when comparing two independent samples. BMC medical research methodology, 12, 1-11.
- Royston, P. (1992). Approximating the Shapiro-Wilk W-test for non-normality. Statistics and computing, 2, 117-119.


コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください