離散一様分布と区分するために連続一様分布と呼ぶ場合もある
区間a-bの範囲内で全ての同じ確率で起こる
確率密度関数:\(
\begin{equation}
f(x) = \left\{
\begin{alignedat}{2}
\frac{1}{b-a} \quad (a \leq x \leq b) \\
0 \qquad \qquad (その他)
\end{alignedat}
\right.
\end{equation}
\)
期待値:\(\dfrac{a+b}{2}\)
分散:\(\dfrac{(b-a)^2}{12}\)
%上記の関数の書き方(TeX)
確率密度関数:\(
\begin{equation}
f(x) = \left\{
\begin{alignedat}{2}
\frac{1}{b-a} \quad (a \leq x \leq b) \\
0 \qquad \qquad (その他)
\end{alignedat}
\right.
\end{equation}
\)確立密度関数
例:\(0 \leq x \leq 6\)

R
#グラフの描き方
plot(
c(1, 6), c(0.2, 0.2),
type="l",
xlim=c(0, 7), ylim=c(0, 0.25),
xlab="", ylab=""
)下図の赤い枠の中の面積が1になります
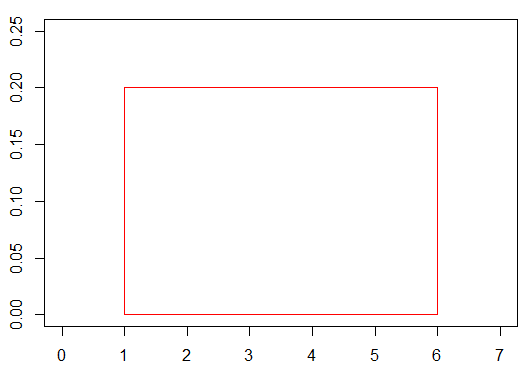
R
#グラフの描き方
plot(
0, 0,
type = "n",
xlim = c(0, 7), ylim = c(0, 0.25),
xlab = "", ylab = ""
)
x <- c(1, 6, 6, 1, 1)
y <- c(0.2, 0.2, 0, 0, 0.2)
lines(x, y, col = "red")おまけ)離散型
サイコロを振った時の出る目Xの確立分布がよく例として挙げられますが、これは離散型一様分布になります
確率:\(P(X=x)=\dfrac{1}{b-a+1} \qquad (a \leq x \leq b)\)
当たり前ですがサイコロの目が1~6になる確率は一様の \(\dfrac{1}{6-1+1}=\dfrac{1}{6}\) ということになります
期待値:\(\dfrac{a+b}{2}\)
分散:\(\dfrac{(b-a+1)^2-1}{12}\)
サイコロの例
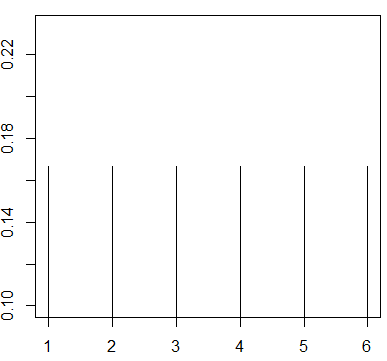
R
#グラウの描き方
x <- c(1:6)
pi <- 1/(6-1+1)
y <- rep(pi, 6)
plot(x, y, type="h")参考文献
- 改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎, ISBN-10 : 4489022271

コメント欄 『間違い』や『分かりにくい部分』などのご意見もお寄せください